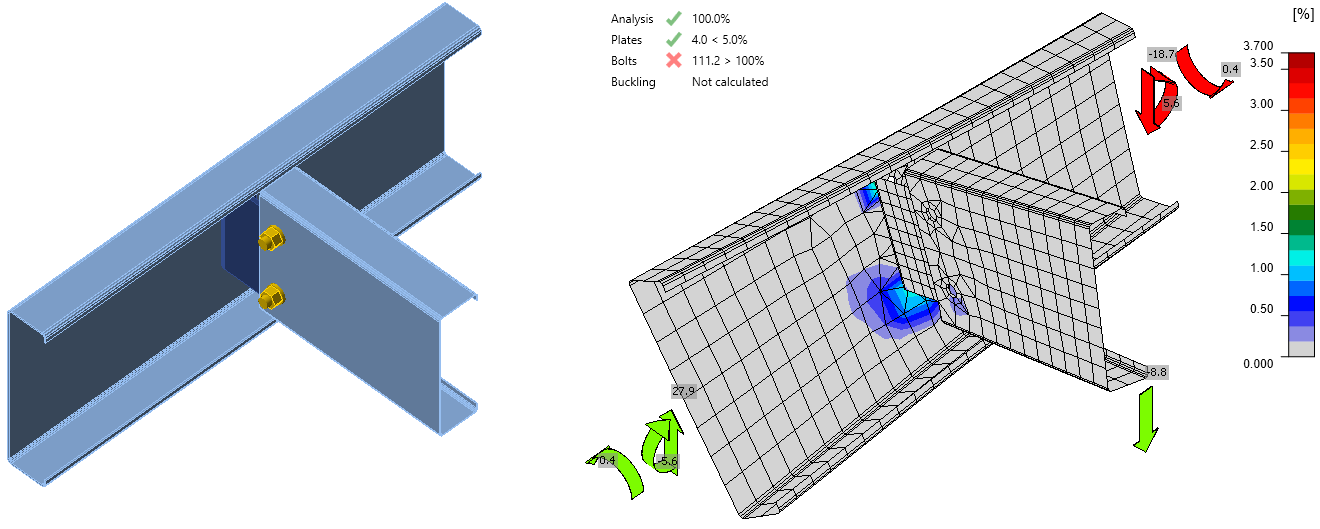
Vervorming van balken - Belasting in het midden van de afschuiving
Beschrijving van het analysemodel
Als de gecondenseerde elementen in het rekenmodel worden opgenomen, worden de staven veel langer. In IDEA StatiCa Connection versie 20.1 en lager hadden de staven standaard een lengte van 1,5×h voor open doorsneden en 2×h voor gesloten doorsneden. De uiteinden van de staven die bestaan uit schaalelementen werden verstijfd door schakels, waardoor de belasting wordt opgelegd. Deze schakels maken het uiteinde van het element stijf bij kromtrekken.
In IDEA StatiCa Connection versie 21.0 en hoger worden de gecondenseerde elementen toegevoegd achter de delen van leden die bestaan uit schaalelementen. Het gecondenseerde element heeft dezelfde eigenschappen als wanneer het is samengesteld uit schaalelementen met elastische materiaaleigenschappen. De lengte van het gecondenseerde element is 4×h voor het spanning-rek analyse type. De belastingen worden opgelegd aan het uiteinde van de gecondenseerde elementen, zodat de verbindingen veel minder worden beïnvloed door de verstijving. Het model is effectiever en maakt het mogelijk om de standaardlengte van een element bestaande uit schaalelementen te verlagen naar 1,25×h voor zowel open als gesloten doorsneden.
Lees meer over dit onderwerp in het artikel Condensed superelements - onzichtbaar maar essentieel.
Dat betekent dat de ledenlengtes met standaardinstellingen toenemen van 1,5×h tot 5,25×h en 2×h tot 5,25×h voor respectievelijk open en gesloten doorsneden. De vervorming ontwikkelt zich door de lengte van het element, volgens de theorie van Vlasov, en het vervormingsmoment neemt niet lineair toe, maar exponentieel.
Dus in eerdere versies (20.1 en lager) had het kromtrekmoment een klein effect, maar nu kan het zeer relevant zijn; het is nu ongeveer 6,5× hoger als de kromtrekking in de verbinding wordt beperkt. Natuurlijk stijgt ook het gebruik van platen, bouten en lassen.
Merk op dat het kromtrekkingmoment afhangt van de lengte van het element, waar de belasting wordt uitgeoefend, randvoorwaarden aan beide uiteinden of enkele tussensteunen of verstijvers. De gebruiker moet zich er dus van bewust zijn dat het krommingsmoment nog steeds onnauwkeurig is. Alleen nu is het lid langer, dus het is dichter bij de werkelijke grootte als de torsie kan worden gerechtvaardigd.
Trekt het element echt krom?
De essentiële vraag is of torsie en kromtrekken van een balk echt mogelijk zijn. Vaak wordt de bovenflens van het element vastgehouden door een vloerplaat die elke torsie van het element effectief tegenhoudt. In dat geval kan de torsie en kromtrekking verwaarloosd worden en is het niet nodig om dit lid en zijn verbinding tegen deze krachten te ontwerpen.
Als de bovenste flenzen van deze spanten echt tegen zijdelingse beweging worden tegengehouden, is deze faalwijze niet relevant en moeten de interne krachten dienovereenkomstig worden aangepast.
Hoe kom je van het ongewenste torsiemoment af?
Er zijn twee manieren om het torsiemoment in de Verbindingstoepassing te verwaarlozen.
Laten we elke optie afzonderlijk bekijken.
Berekening van het equivalente torsiemoment
Alle staven worden belast door hun zwaartepunt. Voor dubbel symmetrische doorsneden (bv. I, H, RHS, CHS-profielen) ligt het zwaartepunt op dezelfde plaats als het afschuifmiddelpunt. Als de belasting door het zwaartepunt gaat, veroorzaakt de dwarskracht geen extra torsie.
Voor andere staven met slechts één of geen symmetrieas verschuift de positie van het zwaartepunt ten opzichte van het zwaartepunt. De afschuifbelasting wordt uitgeoefend door het zwaartepunt en het torsiemoment wordt gegenereerd. Dit torsiemoment is gelijk aan de dwarskracht maal de afstand tussen het zwaartepunt en het afschuifcentrum.
Als een ingenieur aanneemt dat het onderdeel niet kan draaien, moet dit torsiemoment in evenwicht worden gehouden door een tegengesteld torsiemoment in de toegepaste belastingseffecten. Houd er rekening mee dat dit compenserend torsiemoment wordt weergegeven in de onevenwichtskrachten bij gebruik van de optie Belastingen in evenwicht.
Laten we het nu tonen in een praktisch voorbeeld.
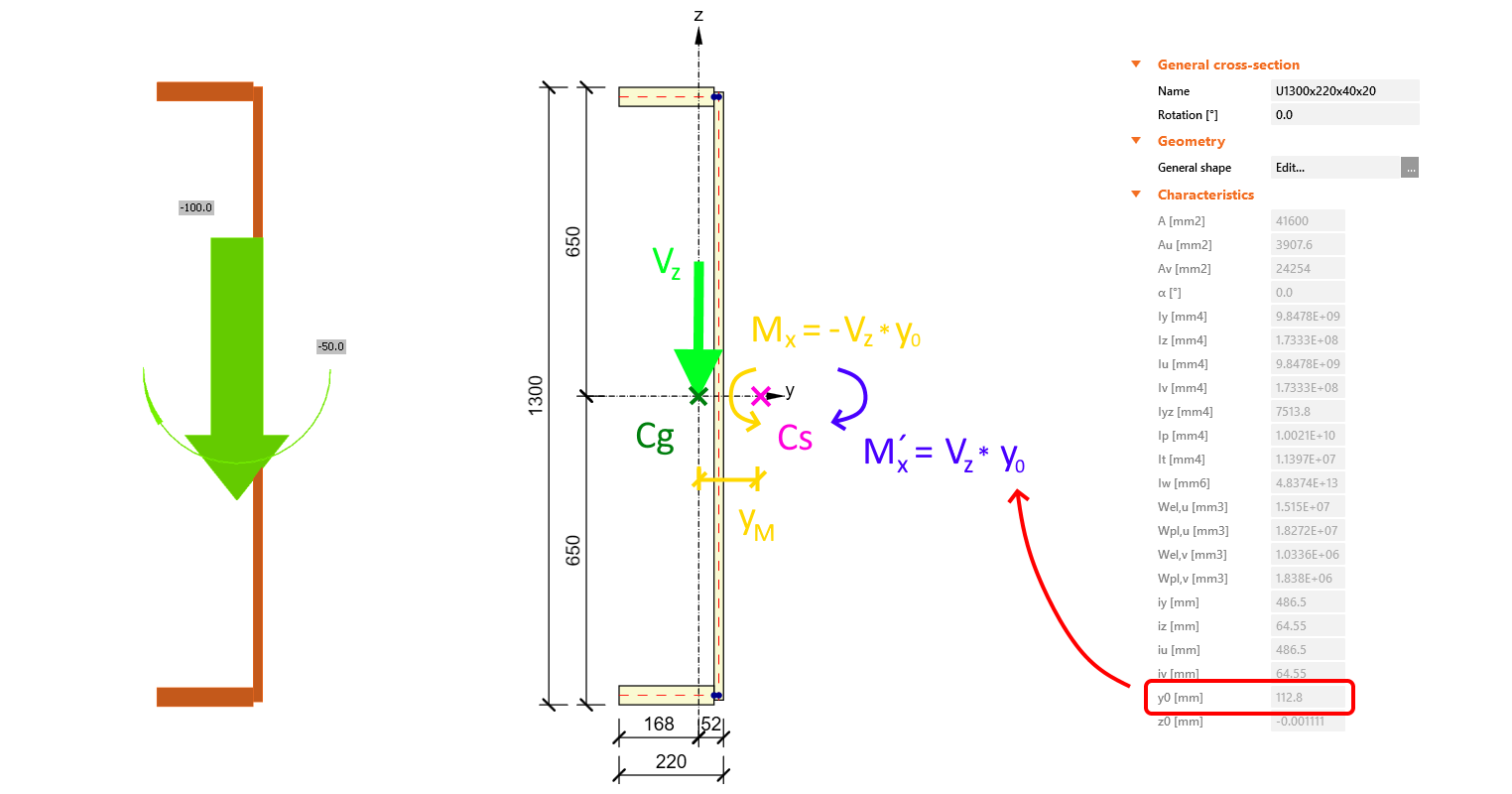
We hebben een verbinding met een U-vormige balk. Bekijk de doorsnede, de eigenschappen en de belastingen in de afbeelding hieronder.
Deze balk wordt bijvoorbeeld verdraaid en vertoont een onrealistische spannings- en vervormingstrend, waardoor de normcontroles worden beïnvloed. In werkelijkheid wordt de balk over de hele lengte tegen torsie beschermd, dus zo'n effect zou er niet moeten zijn.
Om het model te corrigeren, moet een equivalent contra torsiemoment M'x worden berekend en toegevoegd aan de belastingseffecten voor dit lid. In dit voorbeeld, voor LE1, moet het moment M'x = Vz * y0 = 1502 * 0,113 = 170 kNm extra worden toegevoegd.
De beslissing om de torsie al dan niet te balanceren ligt bij de ingenieur. Er zijn clausules in de codes of publicaties die kunnen helpen.
Zijdelingse torsiebeperking
De andere manier om een balk te stabiliseren is door gebruik te maken van de laterale torsie-beperking.
Lees de volgende artikelen voor meer informatie over de functionaliteit: