Leden die een krommingsconstante hebben die niet nul is (I_w) en die op een andere manier belast worden dan door twee identieke torsiemomenten aan hun uiteinden, trekken krom wanneer ze aan torsie worden onderworpen.
Leden in IDEA StatiCa Connection hebben hun fabricagebewerkingen en daarachter standaard 1,25*hvan schaalelementen + 4*h van gecondenseerde elementen; zie het artikel Automatische lengte van leden. Hun lengte is dus eigenlijk niet verwaarloosbaar, maar bedraagt ongeveer een derde van een typische stalen overspanning.
Wanneer torsie wordt toegepast, en dit kan direct zijn door Mx in te voeren of door een afschuifkracht toe te passen op een onsymmetrisch lid, bijvoorbeeld een kanaal of hoek, ontstaan krommingsspanningen.
Torsie veroorzaakt:
- St. Venant torsie, \(T_t\)
- Kromtorsie, T_w
- Bimoment (B)
En deze veroorzaken op hun beurt spanningen:
- Schuifspanning door torsie in St. Venant, \(\tau_{t})
- Schuifspanning als gevolg van kromtrekking, \(\tau_w)
- Normaalspanning door bimoment, \(\sigma_w)
De krachten kunnen worden bepaald door de differentiaalvergelijking op te lossen:
\[EI_w\varphi^{IV}-GI_t\varphi^{II}=m\]
waarbij:
- \(E) - elasticiteitsmodulus in trek en samendrukking
- \(G) - elasticiteitsmodulus in afschuiving
- \(I_w) - kromtrekconstante
- \ Torsieconstante
- \Rotatie
- \torsiemoment
De oplossingen zijn bekend voor ideale randvoorwaarden, bijvoorbeeld vast uiteinde of vrij uiteinde.
De bovengrens van de normaalspanning als gevolg van bimoment voor IDEA StatiCa Connection-elementen is de conditie van een vast uiteinde en een vrij uiteinde waar de belasting (torsie) wordt uitgeoefend.
Voor deze voorwaarde:
\T_t=M \left ( 1-\frac{{\cosh} K_t (1-x/L)}{{\cosh}K_t} \right )\].
\[T_w = M \frac{{\cosh} K_t (1-x/L)}{{\cosh} K_t}}}]
\B=-\frac{ML}{K_t}\frac{{{\sinh} K_t (1-x/L)}{{\cosh} K_t}}]
waarbij:
- \(M) - torsiemoment toegepast aan het uiteinde van het lid(Mx ingesteld in IDEA StatiCa Connection, of dwarskracht V maal afstand tussen middelpunt van afschuiving en zwaartepunt)
- \(K_t = L \sqrt{frac{GI_t}{EI_w}})
- \(L) - lengte van het lid (cantilever)
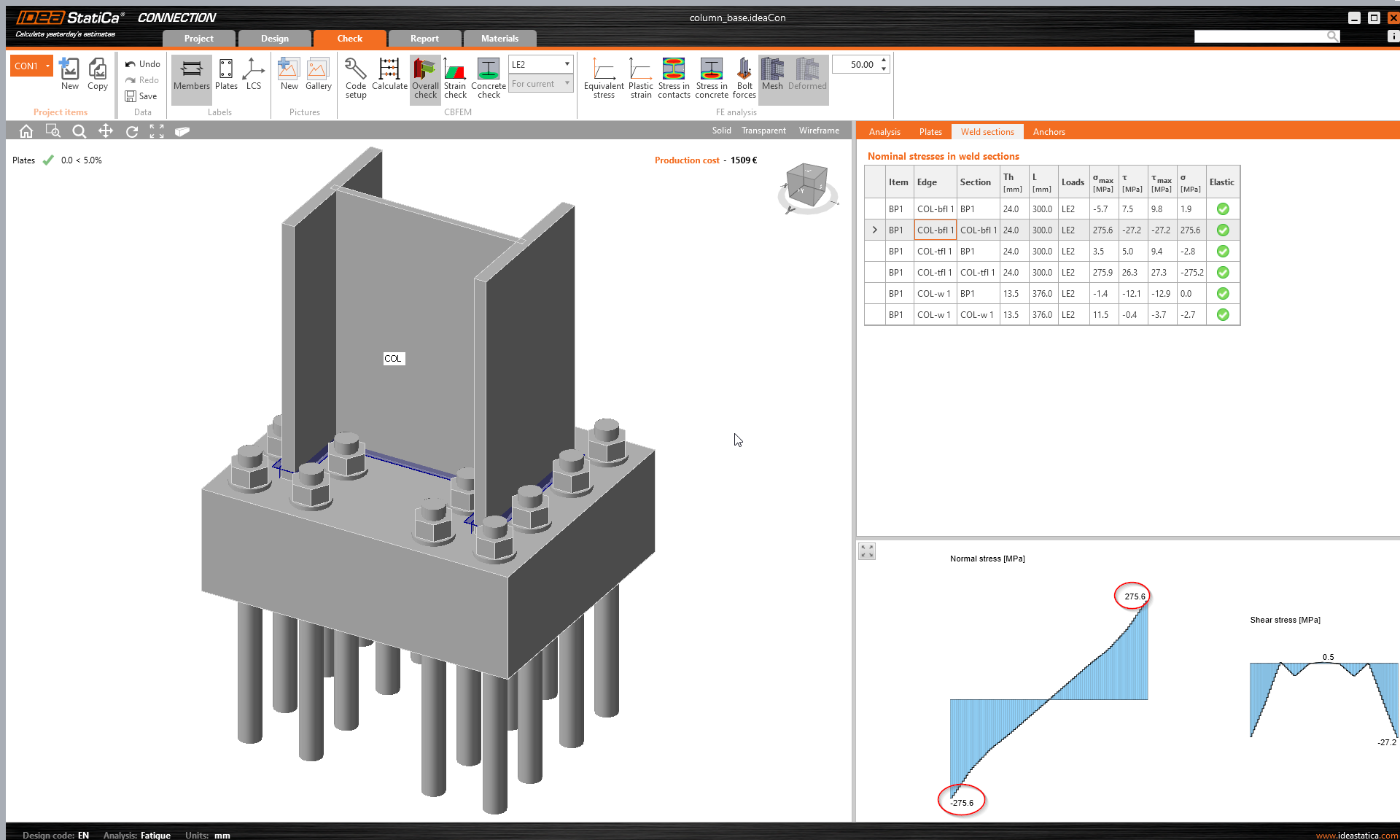
Hier is een voorbeeld van een echt stijve verbinding:
De kolom wordt belast door een torsiemoment (M_x = 30,\textrm{kNm}). Hoewel de voetplaat erg dik is, vervormt deze toch een beetje door het kromtrekken van de kolom. Dit veroorzaakt trekkrachten in ankers en drukspanning in beton. Dat betekent dat de kromtrekbeperking nog steeds niet perfect is. Zoiets kunnen we in de echte wereld echter niet verwachten.
Met behulp van vermoeiingsanalyse kunnen we normale en afschuifspanningen uitzetten in de buurt van de stuiklas (op een afstand van 0,5 keer de dikte van de lasdoorn):
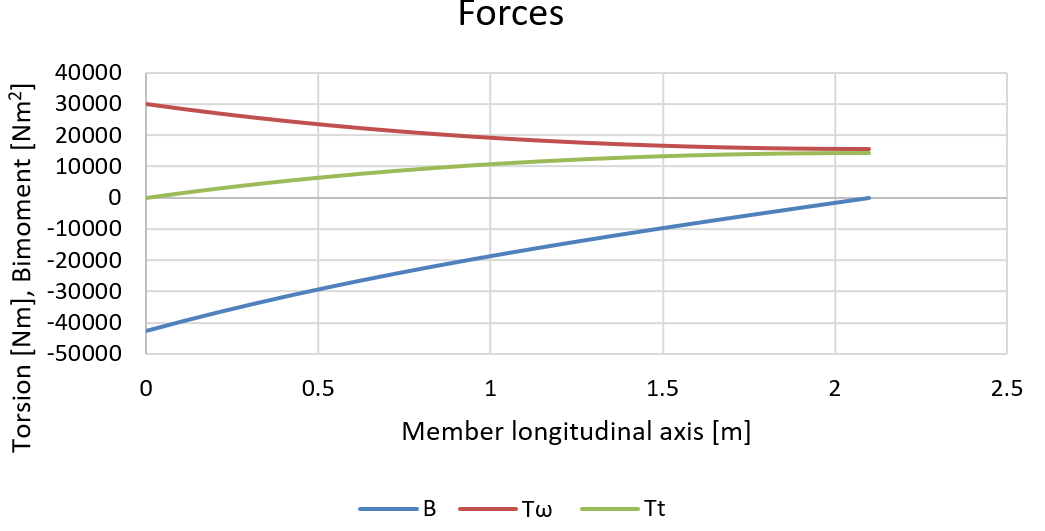
Laten we de spanningen vergelijken met een analytische oplossing. Met behulp van de bovenstaande formules zijn de krachten:
En de bijbehorende spanningen op de kolomflens kunnen worden berekend:
\tau_t=T_t \frac{t_f}{I_t}].
\tau_w= T_w \frac{S_{omega,max}}{I_w t_f} \]
\[\sigma_w=B \frac{\omega}{I_w}\]
De pieknormale spanning veroorzaakt door kromtrekken op de locatie van de bodemplaat (Lid lengteas = 0 in grafieken) bereikt 314 MPa, wat iets hoger is dan de resultaten die we krijgen in IDEA StatiCa. Dit verschil wordt veroorzaakt door imperfecte kromtrekbeperking. De schuifspanningen bij de verbinding tussen de elementen (in dit geval de kolomvoet) zijn verwaarloosbaar.
De spanningsverdeling langs de doorsnede als gevolg van torsie en kromtrekken kan worden bekeken in de algemene doorsnede-editor:
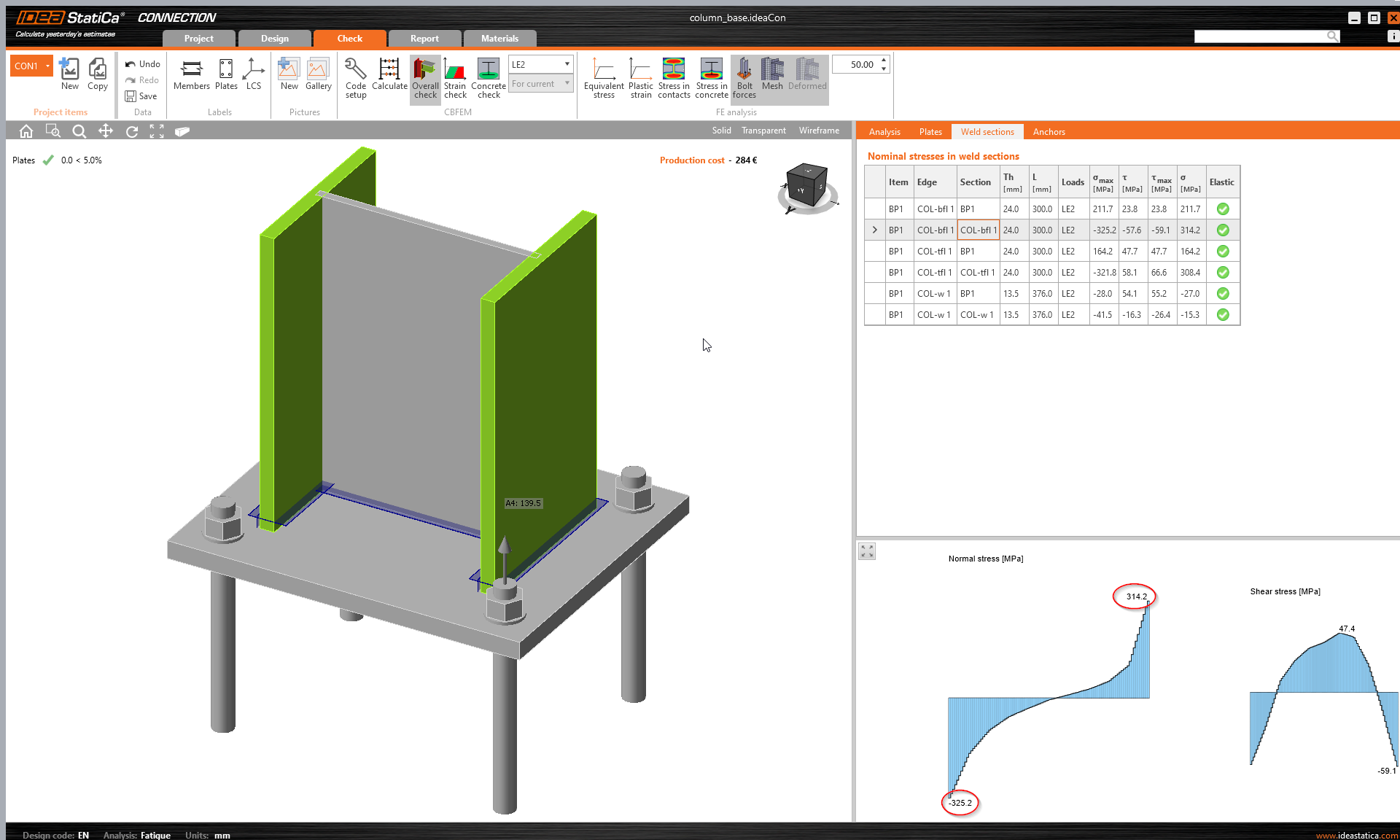
Een voorbeeld uit de praktijk is lastiger uit te leggen. Laten we de dikte van de voetplaat veranderen in 30 mm en slechts vier ankers M36 8.8 gebruiken:
Nu vervormt de voetplaat aanzienlijk, de spanning in het beton is niet verwaarloosbaar en de kracht in het anker is in feite enorm, bijna 140 kN (vergelijk met N_{Rd,s} = 370,4, \textrm{kN}} bepaald door EN 1992-4). De normale spanningen als gevolg van kromtrekken zijn niet langer lineair zoals volgens de analytische oplossing als gevolg van de vervorming van de bodemplaat. Een beetje verrassend is dat de piekspanning van 314 MPa gelijk is aan de analytische oplossing.
Conclusie
Ingenieurs hebben de neiging om torsie-effecten, vooral kromtrekken, te negeren of te vermijden, bv. door gesloten doorsneden te gebruiken. Merk op dat software die 1D-elementen gebruikt meestal zes vrijheidsgraden heeft (3 translaties, 3 rotaties), en om kromtrekken vast te leggen hebben ze een zevende nodig. 1D-elementen met zeven vrijheidsgraden zijn bijvoorbeeld beschikbaar in LTBeam of Consteel. Zelfs dan is het moeilijk om te bepalen hoe vervorming wordt overgedragen door verbindingen van het ene element naar het andere. Toch is kromtrekken een reëel fenomeen en open doorsneden zijn erg gevoelig voor de effecten ervan.
Wees voorzichtig bij het toepassen van torsie op elementen met een open doorsnede. Als dit onderdeel faalt in IDEA StatiCa Connection, zou dat een rode vlag moeten zijn voor een ingenieur. Torsie inclusief kromtrekken moet worden geëvalueerd in het ontwerp van het element, bijvoorbeeld met behulp van IDEA StatiCa Member met echte lengte en krachten toegepast op de juiste locaties.