Il CSFM spiegato

In pratica, per progettare le regioni di discontinuità nelle strutture in calcestruzzo armato e precompresso si utilizzano normalmente i metodi Strut-and-Tie (S&T) e Stress Fields. Il Metodo dei Campi di Sollecitazione Compatibile (CSFM) è stato sviluppato estendendo queste teorie classiche, consentendo un elevato grado di automazione ed è coerente con gli standard di progettazione. Nonostante la sua semplicità, il metodo fornisce una descrizione molto realistica della risposta di una struttura in calcestruzzo sia allo stato limite ultimo (ULS) che allo stato limite di servizio (SLS). Il CSFM è implementato in IDEA StatiCa Detail.

Fig. 1 a) Parete con aperture b) Parete a taglio c) Trave con estremità tagliate e aperture d) Pilastro del ponte e) Diaframma del ponte

Le procedure standard per la progettazione delle sezioni trasversali delle strutture in calcestruzzo sono applicabili nelle parti in cui vale l'ipotesi di Bernoulli-Navier della distribuzione piana delle deformazioni (regione B). I punti in cui questa ipotesi non si applica sono chiamati regioni di discontinuità (regioni D). Queste includono le parti delle strutture in cui compaiono carichi concentrati o in cui si verifica un improvviso cambiamento della sezione trasversale, come le estremità a cuneo (Fig. 1c), le travi profonde, le pareti con aperture (Figg. 1a, 1b), o le mensole e le calotte delle pile. Nel campo dell'ingegneria dei ponti, si tratta ad esempio delle calotte delle pile (Fig. 1d), dei diaframmi (Fig. 1e), dei deviatori, ecc.

1. Metodo del puntone e della cravatta

L'ipotesi di base per la definizione di un modello S&T è che si trascuri la resistenza a trazione del calcestruzzo. Un semplice modello di capriata è costituito da elementi che agiscono in compressione e in trazione, rappresentando il comportamento ULS. In generale, non si tratta di un problema complesso e la definizione di un modello S&T di base (Fig. 2a) non dovrebbe essere un problema per un ingegnere esperto. Tuttavia, anche per questo compito di base, la corretta valutazione del modello in conformità allo standard di progettazione può essere un processo tedioso, manuale e iterativo.

Fig. 2 a) Modello di S&T opzione 1 b) Modello di S&T opzione 2 c) Modello di S&T opzione

È necessario valutare i vincoli, le aree nodali e la deformazione trasversale a trazione dei puntoni. Se il modello non supera la verifica, è necessario modificare la geometria S&T o scegliere un modello S&T diverso (Fig. 2b, 2c). Questo spesso porta l'ingegnere strutturale a scegliere la geometria del modello S&T solo una volta e a valutare solo l'armatura. Questo può portare a un errore sostanziale. La scelta del modello è sempre una questione di esperienza. Per i dettagli strutturali più complessi, la scelta di un S&T che corrisponda sufficientemente al comportamento effettivo della struttura può non essere così facile come nel caso precedente. Inoltre, l'S&T è un metodo per la progettazione dei soli stati limite ultimi. Non consente di progettare gli stati limite di servizio (deformazione, fessurazione), che sono criteri critici, soprattutto in strutture di notevole importanza, in quanto hanno un impatto diretto sulla vita utile della struttura.

2. Metodo del campo di sollecitazione compatibile - CSFM

Il CSFM è un moderno metodo non lineare per l'analisi delle regioni D e degli elementi il cui comportamento può essere semplificato alle sollecitazioni piane, cioè a un modello 2D. Tuttavia, si basa ancora su un'assunzione di base e sicura delle norme: il calcestruzzo non agisce in tensione e tutte le tensioni devono essere trasferite dall'armatura. Il Compatible Stress Field Method (CSFM) è un'evoluzione dei metodi S&T e del campo di sollecitazione, eliminando i loro principali svantaggi sopra menzionati: incertezze nella selezione del modello, difficoltà nell'automazione e incapacità di valutare gli stati limite di servizio.

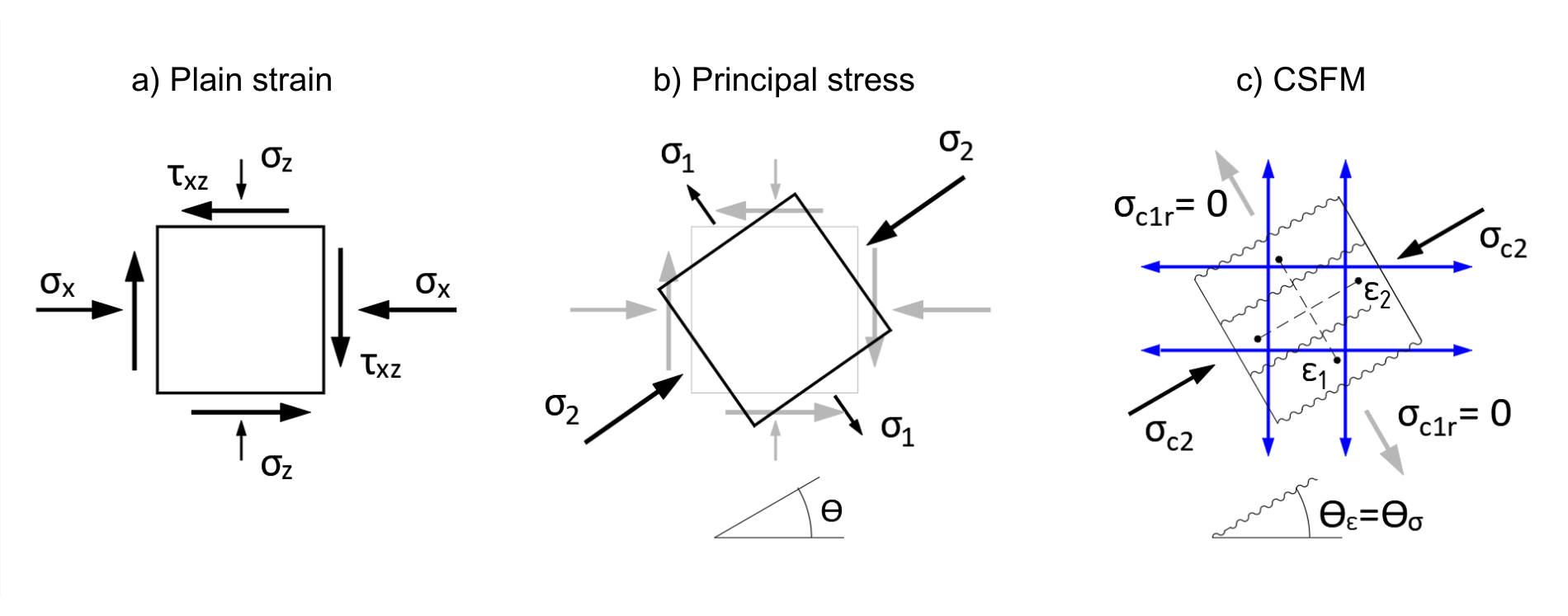
Fig. 3 a) Deformazione semplice b) Sollecitazione principale c) CSFM

Il principio del CSFM può essere spiegato sulla sollecitazione semplice dell'elemento piano di base di una struttura in cemento armato. La Fig. 3a mostra l'elemento 2D di base in sollecitazione semplice, così come lo conosciamo da tutti i libri di testo sull'elasticità e la resistenza. Si tratta della sollecitazione in un punto della struttura, ottenuta, ad esempio, mediante analisi elastica lineare con il metodo degli elementi finiti (FEM). L'elemento è soggetto a uno sforzo normale orizzontale _σx, a uno sforzo normale verticale _σz e a uno sforzo di taglio _τxz. Da queste sollecitazioni si possono determinare le cosiddette sollecitazioni principali e la loro direzione definita dall'angolo θ (Fig. 3b). L'elemento è quindi sottoposto alla sollecitazione principale di trazione _σ1 e alla sollecitazione principale di compressione _σ2.

Come apparirà la deformazione dello stesso elemento analizzato con il CSFM? La deformazione è mostrata nella Figura 3c. Il calcestruzzo compresso appare nella direzione della sollecitazione principale di compressione _σ2. Viene generato un campo di sollecitazione con sollecitazione _σc2. Come già detto, l'ipotesi di base è che il calcestruzzo non agisca in tensione. Pertanto, la sollecitazione principale trasversale di trazione _σ1 non sarà trasferita dal calcestruzzo e si formerà una fessura perpendicolare alla direzione. La sollecitazione _σc1r deve quindi essere pari a zero. Per evitare il fallimento del nostro elemento 2D, tutte le tensioni di trazione devono essere trasferite dall'armatura (indicata in blu nella Fig. 3c), che deve far parte del modello di calcolo.

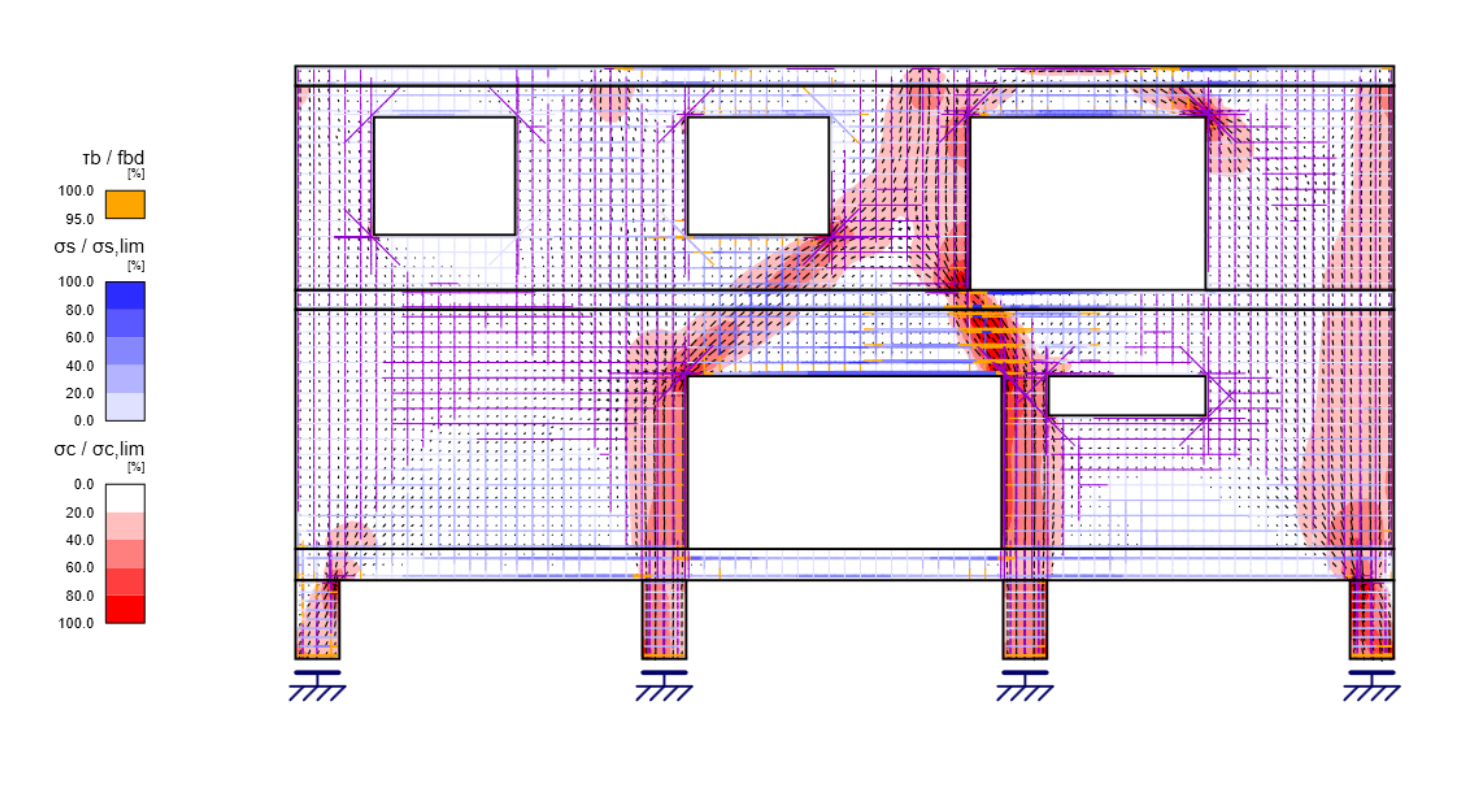
Se l'analisi delle sollecitazioni viene eseguita con il CSFM in modo continuo sull'intera regione 2D da risolvere, il risultato è un campo di compressione continuo nel calcestruzzo più le sollecitazioni di trazione e compressione nell'armatura. Una rappresentazione grafica semplificata del campo di sollecitazioni CSFM è mostrata nella Figura 4. Oltre ai tassi di utilizzo del calcestruzzo e delle armature, la figura indica anche le direzioni variabili delle sollecitazioni calcolate _σc2 lungo le regioni.

Fig. 4 Risultati complessivi del dettaglio IDEA StatiCa

L'analisi di un dettaglio o di una struttura utilizzando il CSFM si basa sul metodo degli elementi finiti. Il calcestruzzo è modellato con elementi parete 2D e l'armatura con elementi membro 1D (Fig. 7). L'analisi non viene eseguita in un'unica fase, poiché si tratta di un problema non lineare. I carichi vengono applicati in modo incrementale durante il calcolo e la soluzione del sistema di equazioni non lineari viene trovata con il metodo di Newton-Raphson.

Le cricche fittizie (_ε1 è il valore medio) si "formano" perpendicolarmente alla direzione delle tensioni principali, che possono cambiare durante il calcolo non lineare in quanto l'elemento "si fessura progressivamente" a ogni incremento di carico. In sintesi, si considera una cricca rotante fittizia priva di tensioni.

Il risultato della soluzione FEM utilizzando il CSFM è un campo di sollecitazioni compatibile (cioè il calcestruzzo non si rompe in singoli puntoni che agiscono indipendentemente nel modello) e lo stato di deformazione, che sono continui in tutto il dominio 2D da risolvere. Questo è un grande vantaggio rispetto ai classici approcci S&T e permette di automatizzare e raffinare il modello computazionale, come descritto nei paragrafi seguenti.

Fig. 5 Principio del rammollimento del calcestruzzo

La semplice formulazione del CSFM consente di utilizzare il diagramma sforzi-deformazioni parabolico-rettangolare uniassiale standard per il calcestruzzo in compressione secondo la norma di progetto. Come è noto, la resistenza a compressione del calcestruzzo diminuisce quando il calcestruzzo è danneggiato da fessure trasversali (Fig. 5). Questo cosiddetto effetto di ammorbidimento a compressione è incluso nel metodo tenendo automaticamente conto della resistenza effettiva a compressione del calcestruzzo.

In base al livello delle deformazioni trasversali di trazione _ε1, si determina il fattore di riduzione _kc e si regola il diagramma sforzo-deformazione del calcestruzzo (Fig. 5). Essendo noto il campo di deformazioni dell'intera struttura, la resistenza effettiva a compressione del calcestruzzo può essere calcolata automaticamente nelle singole sezioni in funzione del livello locale delle deformazioni trasversali a trazione _ε1.

Fig. 6 Principio di irrigidimento a trazione

Inoltre, il CSFM considera l'effetto di irrigidimento del calcestruzzo in trazione tra le fessure sull'armatura, il cosiddetto irrigidimento per trazione. Nel modello di calcolo si utilizza il rapporto di armatura medio _εm. Quindi il diagramma sforzo-deformazione dell'armatura viene modificato (Fig. 6). Ciò consente una rappresentazione realistica della rigidezza di una struttura in calcestruzzo armato danneggiata da fessure. Tuttavia, è ancora vero che la resistenza a trazione del calcestruzzo non contribuisce alla capacità ultima. La sollecitazione massima nell'armatura _σsr nelle fessure è fondamentale per la progettazione (Fig. 6).

Il CSFM utilizza i comuni modelli monoassiali dei materiali (diagrammi sforzo-deformazione) definiti nelle norme di progettazione. L'approccio standard, il metodo del fattore di sicurezza parziale, viene quindi utilizzato per valutare l'ULS. La semplicità del metodo lo rende adatto alla pratica ingegneristica e coerente con le norme di progettazione.

Anche se si tratta di un'analisi FEA non lineare, l'ingegnere strutturale non deve inserire nel calcolo ulteriori proprietà del materiale e caratteristiche del calcestruzzo che potrebbero non essere disponibili in fase di progettazione e che sono necessarie, ad esempio, per le analisi FEA non lineari basate sulla meccanica della frattura. Come già indicato, uno dei principali vantaggi dell'analisi CSFM, oltre agli stati limite ultimi, è la capacità di valutare gli stati limite di servizio: deflessioni, limitazioni delle sollecitazioni e, in particolare, larghezza delle fessure.

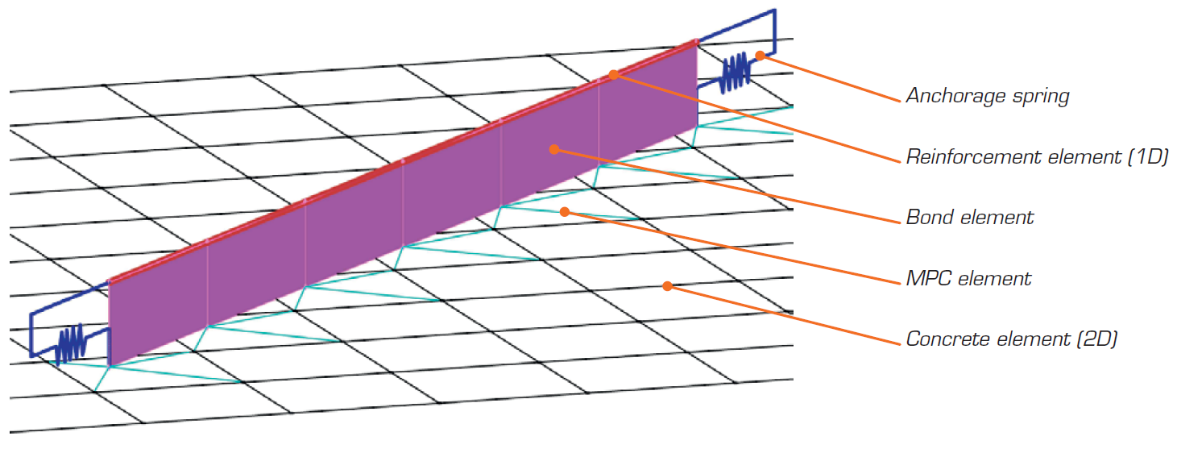
Fig. 7 Esempio di rappresentazione del modello agli elementi finiti in IDEA StatiCa Detail

(Fig. 7) Il modello FEM in CSFM è composto da diversi tipi di elementi finiti:

• elemento 1-D con rigidezza assiale per le armature
• elemento isoparametrico 2-D per il calcestruzzo
• Molle di estremità per il modello di ancoraggio delle armature con trattamento di estremità
• elemento speciale 2-D per modellare la coesione tra armatura e calcestruzzo
• Vincoli rigidi e interpolanti (Multi-Point Constraints, MPC) tra gli elementi di coesione e il calcestruzzo

Se l'armatura progettata previene la rottura fragile dell'elemento, il CSFM ha dimostrato di fornire ottime previsioni della risposta e della capacità ultima della struttura, nonostante la semplicità della formulazione. In altre parole, il metodo non è adatto, ad esempio, per la progettazione di travi senza armatura trasversale a taglio che presentano un comportamento potenzialmente fragile. Le verifiche del metodo, compresi gli esperimenti, sono riportate in [1]. Una descrizione più dettagliata del metodo esula dagli scopi del presente documento e può essere trovata anche in Background teorico.

È chiaro che i principi del CSFM sono generali e quindi la sua applicazione non è limitata alle regioni D, ma può essere utilizzata per modellare intere membrature, ad esempio travi prefabbricate, e dove l'elemento può essere semplificato a un modello 2D planare. Il metodo e la sua implementazione nel software (IDEA StatiCa Detail) sono stati inoltre estesi, con la possibilità di specificare le armature precompresse e post-tese.

3. Esempio di progettazione della calotta di un pilastro

L'applicazione pratica del CSFM è mostrata nella progettazione della calotta del pilastro del ponte nella Figura 8. Si tratta del secondo pilastro di un'opera di ingegneria civile. Si tratta del secondo pilastro di un ponte continuo con tre campate di 30,0 m, 42,0 m e 30,0 m. La testa del pilastro in cemento armato è progettata in calcestruzzo C40/50 e il suo spessore (nella direzione longitudinale del ponte) è di 2,0 m.

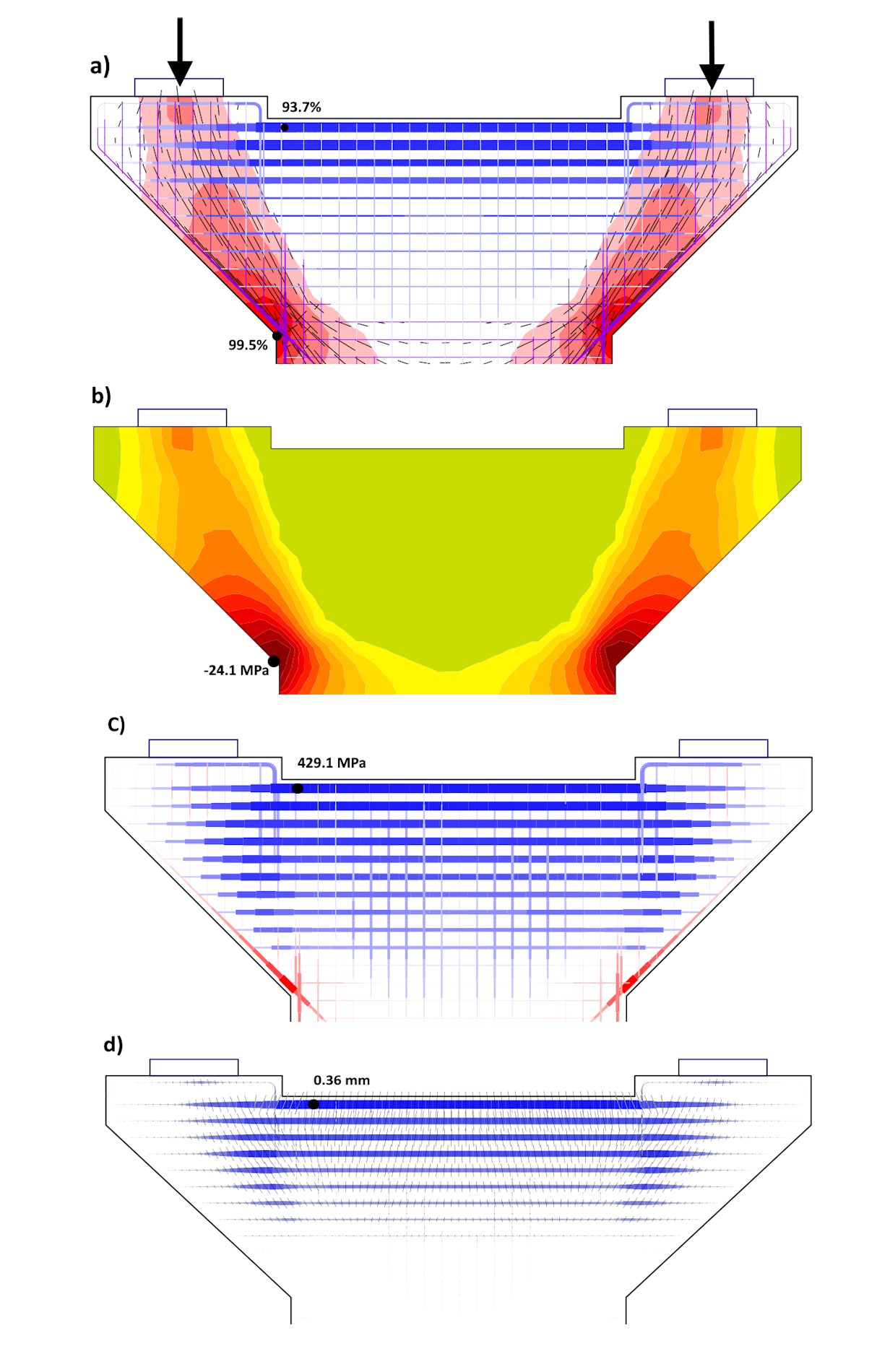
Fig. 8 Cima del pilastro: a) Progetto di sintesi; b) Sollecitazione di compressione nel calcestruzzo in ULS; c) Sollecitazione di trazione nell'armatura in ULS; d) Larghezza della fessura in SLS

Alla sommità della calotta del molo è stata progettata una trave trasversale con armatura B500 20xϕ28+20xϕ25 - i quattro strati superiori. La Figura 8a mostra una sintesi del progetto allo stato limite ultimo, con l'indicazione delle tensioni di compressione nel calcestruzzo, delle direzioni delle tensioni di compressione e delle tensioni nelle armature. La distribuzione più dettagliata delle sollecitazioni nel calcestruzzo e nelle armature è documentata nelle Figure 8b e 8c. L'armatura trasversale è appena al di sotto del limite di snervamento e le sollecitazioni nel calcestruzzo (e le relative deformazioni) sono soddisfacenti all'ULS. Tuttavia, il risultato del calcolo dell'ampiezza della fessura (Fig. 8d) mostra che il progetto non soddisfa lo SLS: _wmax = 0,36 mm > _wlim = 0,3 mm. Per soddisfare la larghezza di fessura limite, è necessario aumentare l'armatura della traversa a 20xϕ32+20xϕ28. Nel caso di _wlim = 0,2 mm (ad esempio, pontile vicino a una strada che genera nebbia salina, livello di influenza ambientale XF2), l'armatura della traversa dovrebbe essere aumentata addirittura a 24xϕ32+24xϕ28.

Conclusione

Il CSFM è adatto alla pratica ingegneristica perché utilizza modelli di materiali semplici definiti in uno standard di progettazione. Oltre agli stati limite ultimi, consente di progettare anche gli stati limite di esercizio. Per i quali, in precedenza, la valutazione era difficile da immaginare quando si utilizzavano modelli S&T. Implementando il metodo in IDEA StatiCa Detail, è possibile catturare realisticamente la risposta della struttura e progettare e valutare le regioni di discontinuità e gli assiemi più grandi in modo efficiente e sicuro.

Il CSFM è stato sviluppato principalmente grazie al lavoro del professor Walter Kaufmann, responsabile della cattedra di Ingegneria strutturale del Politecnico federale di Zurigo. Lui e il suo team hanno anche verificato il metodo e la sua implementazione software.

Letteratura

[1] KAUFMANN, Walter e altri: Compatible stress field design of structural concrete, ETH Zurich, 2020, ISBN 978-3-906916-95-8,

[2] KAUFMANN, W., MARTI, P.: Calcestruzzo strutturale: Modello a membrana fessurata. Journal of Structural Engineering 124 (12): 1467-75, 1998 https://doi.org/10.1061/(ASCE)0733-9445(1998)124:12(1467)

[3] KRAUS, M., M. WEBER, W. KAUFMANN, W, BOBEK, L.: Analisi numerica di angoli di telai testati sperimentalmente con momenti di apertura utilizzando il Compatible Stress Field Method (CSFM). In: Computational Modelling of Concrete and Concrete Structures, pp. 694-03. CRC Press, 2022 https://doi.org/10.1201/9781003316404

Autore

Ing. Pavel Kaláb, Ph.D.

IDEA StatiCa s.r.o.