Analisi di buckling (EN)

La resistenza al carico dei componenti sottili può essere determinata mediante una combinazione di analisi di instabilità lineare e analisi materialmente non lineare.

Esistono cinque categorie di analisi strutturale agli elementi finiti con le seguenti ipotesi:

1. Materiale lineare, geometricamente lineare
2. Materiale non lineare, geometricamente lineare
3. Materiale lineare, perdita di stabilità lineare - buckling
4. Materiale lineare, geometricamente non lineare con imperfezioni
5. Materiale non lineare, geometricamente non lineare con imperfezioni

Una procedura di progettazione che combina gli approcci 2 e 3 - analisi della non linearità del materiale e della stabilità - è menzionata nel Capitolo 8 della norma EN 1993-1-6. La verifica della resistenza all'instabilità sulla base dei risultati FEM ottenuti è descritta nell'Allegato B della norma EN 1993-1-5. Questa procedura è utilizzata per un'ampia gamma di materiali. Questa procedura viene utilizzata per un'ampia gamma di strutture, ad eccezione dei gusci molto sottili, per i quali è più adatta un'analisi geometrica non lineare con imperfezioni iniziali (4 e 5).

La procedura utilizza amplificatori di carico α, ottenuti come risultati dell'analisi FEM, che consentono di prevedere la resistenza post-buckling dei giunti.

Il coefficiente di carico, αult_,k, è determinato dal raggiungimento della capacità plastica senza considerare la non linearità geometrica. La verifica della capacità plastica e la determinazione automatica generale di αult_,k sono implementate nel software sviluppato.

Viene determinato il fattore critico di instabilità, _αcr, che si ottiene utilizzando l'analisi FEM della stabilità lineare. Viene determinato automaticamente nel software utilizzando lo stesso modello FEM utilizzato per il calcolo di αult_,k. Si noti che il punto critico in termini di resistenza plastica non è necessariamente valutato nel primo modo critico di instabilità. In un giunto complesso è necessario valutare più modi di instabilità, perché sono legati a diverse parti del giunto.

Si determina la snellezza non dimensionale della piastra, \( \bar \lambda_p \), del modo di instabilità esaminato:

\[ \bar \lambda_p = \sqrt{\frac{\alpha_{ult,k}}{\alpha_{cr}}} \]

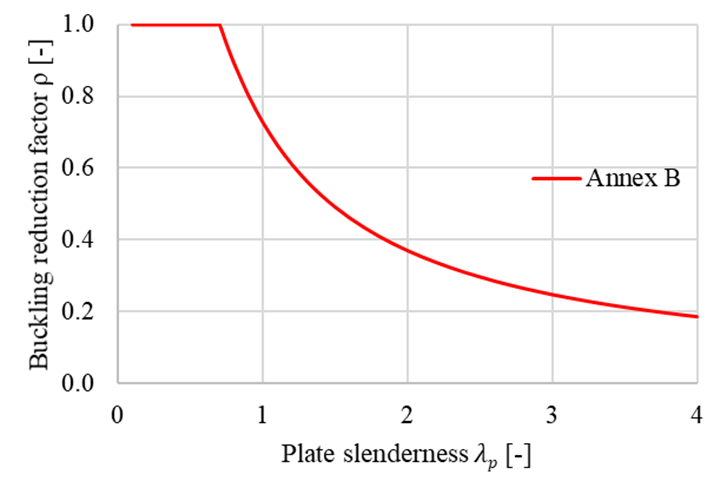
Il fattore di riduzione dell'instabilità ρ è determinato in base all'Allegato B della norma EN 1993-1-5. Il fattore di riduzione dipende dall'inclinazione della piastra. Il fattore di riduzione dipende dalla snellezza della piastra. La curva di instabilità utilizzata mostra l'influenza del fattore di riduzione sulla snellezza della piastra. Il fattore di instabilità fornito applicabile alle membrature non uniformi si basa sulle curve di instabilità di una trave. La verifica si basa sul criterio di snervamento di von Mises e sul metodo delle sollecitazioni ridotte. La resistenza all'instabilità è valutata come

\[ \frac{\alfa_{ult,k} \rho}{\gamma_{M2}} \ge 1 \]

Fattore di riduzione dell'instabilità ρ secondo EN 1993-1-5 Allegato B

Sebbene il procedimento sembri banale, è generale, robusto e facilmente automatizzabile. Il vantaggio della procedura è l'analisi FEM avanzata dell'intero giunto, che può essere applicata alla geometria generale. Inoltre, è inclusa negli standard Eurocode validi. L'analisi numerica avanzata fornisce una rapida panoramica del comportamento globale della struttura e delle sue parti critiche e consente un rapido irrigidimento per prevenire le instabilità.

La snellezza limite, λ_p, è riportata nell'Allegato B della norma EN 1993-1-5 e definisce tutti i casi che devono essere valutati secondo la procedura precedente. La resistenza è limitata dall'instabilità per le piastre con una snellezza maggiore di 0,7. Al diminuire della snellezza, la resistenza è governata dalla deformazione plastica. Il fattore di instabilità critico limite per la snellezza della piastra è pari a 0,7, e la resistenza all'instabilità pari alla resistenza plastica può essere ottenuta come segue

\[ \alpha_{cr} = \frac{\alpha_{ult,k}}{bar \lambda_p^2} = \frac{1}{0,7^2} = 2,04 \]

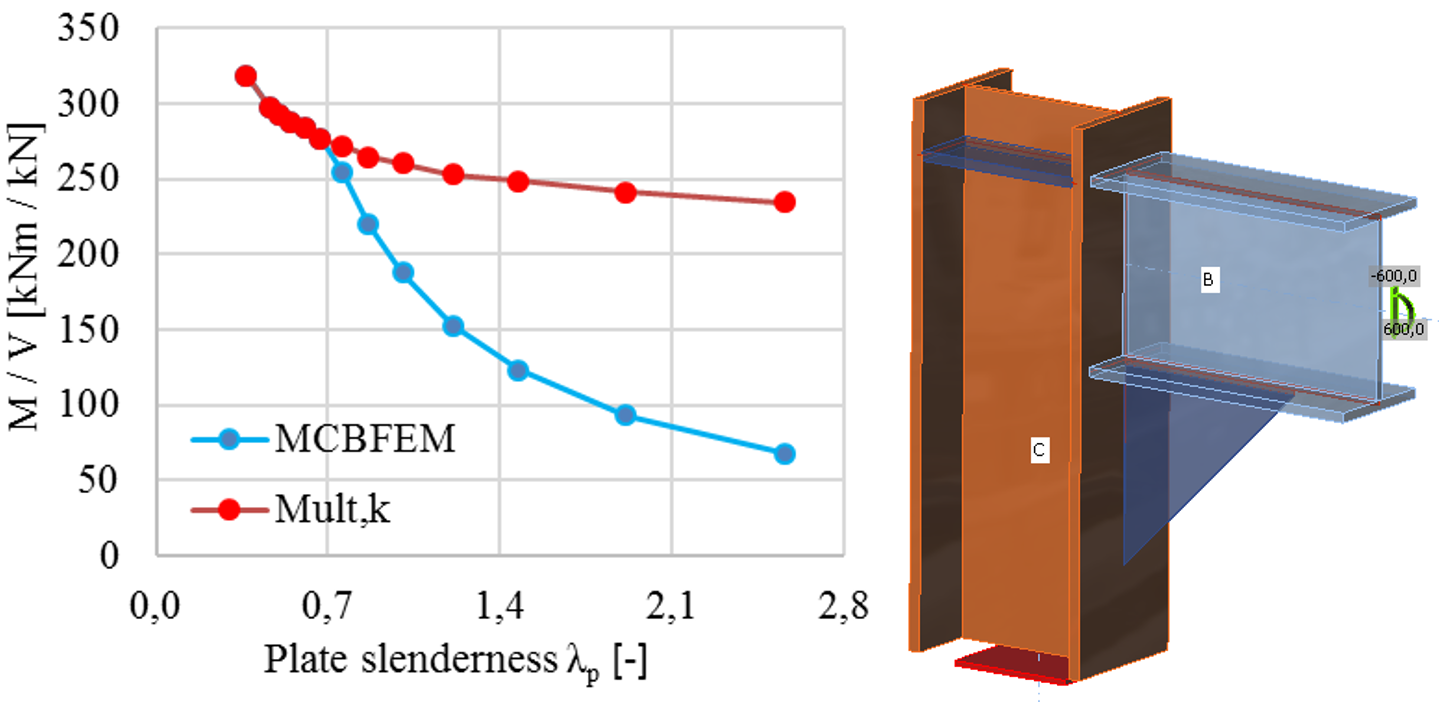
L'influenza della snellezza della piastra sulla resistenza plastica,_Mult,k, e sulla resistenza all'instabilità,_MCBFEM, è mostrata nella figura seguente. Il diagramma mostra i risultati di uno studio numerico di un irrigidimento triangolare in un giunto a portale.

L'influenza della snellezza della piastra sulla resistenza di un giunto a telaio a portale con irrigidimento sottile