IDEA StatiCa RCS - Cálculo estructural de elementos de hormigón 1D

Diseño de secciones de hormigón armado según EN 1992-1-1 y EN 1992-2.

Flexión
Cortante
Torsión
Interacción
Comprobación de la limitación de esfuerzos
Control de fisuras
Diagrama N-M-κ
Bibliografía

Doblar

Métodos de comprobación de la capacidad seccional

Para comprobar el estado límite último de elementos de hormigón 1D se pueden utilizar dos métodos bien conocidos. El primero nos dará la capacidad última de la sección transversal en forma de área de interacción o diagrama de interacción (en el caso de momento flector en una dirección).La capacidad de la sección transversal puede determinarse como la relación entre las fuerzas internas actuantes y las fuerzas del estado límite. La segunda consiste en encontrar el equilibrio en una sección transversal, donde buscamos el comportamiento real de la sección cargada, el uso de materiales en términos de tensiones y una visión de las vulnerabilidades de la sección.

Supuestos generales de diseño e hipótesis de cálculo para el Estado Límite Último

1. La deformación ε en la armadura y el hormigón se supondrá directamente proporcional a la distancia desde el eje neutro (las secciones planas permanecen planas).
2. La interacción de la armadura y el hormigón se garantiza mediante la interacción del hormigón y la armadura sin deslizamiento (la deformación ε soporta la deformación en las fibras adyacentes del hormigón son iguales).
3. La resistencia a tracción del hormigón se desprecia (todas las tensiones de tracción se transmiten por la armadura).
4. Las tensiones de compresión del hormigón en la zona de compresión se calculan en relación con la deformación calculada a partir de los diagramas tensión-deformación.
5. Las tensiones de la armadura se calculan en función de la deformación a partir de los diagramas tensión-deformación.
6. La deformación de compresión del hormigón con un límite de deformación última _εcu2 (diagrama parábola-rectángulo para hormigón sometido a compresión) y _εcu3 (relación bi-lineal tensión-deformación),[2].
7. La deformación a compresión de la armadura es ilimitada en el caso de la rama superior plástica horizontal, en el caso de la rama superior plástica inclinada la deformación está limitada _εud,[2].
8. Se considera un estado límite cuando el estado de al menos uno de los materiales supera la deformación límite última (si εu no está limitada, rige el hormigón comprimido).

\[ \textsf{\textit{footnotesize{\qquad Tensión de deformación.}}]

\Diagrama de diseño tensión-deformación para acero de refuerzo con rama superior inclinada.

Diagrama de interacción

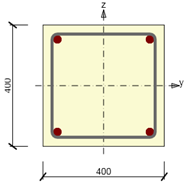
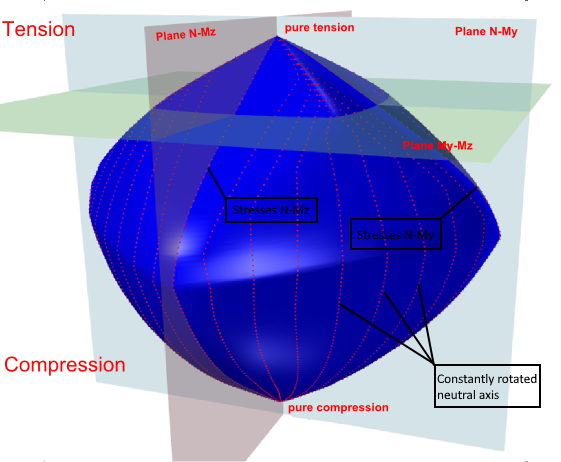
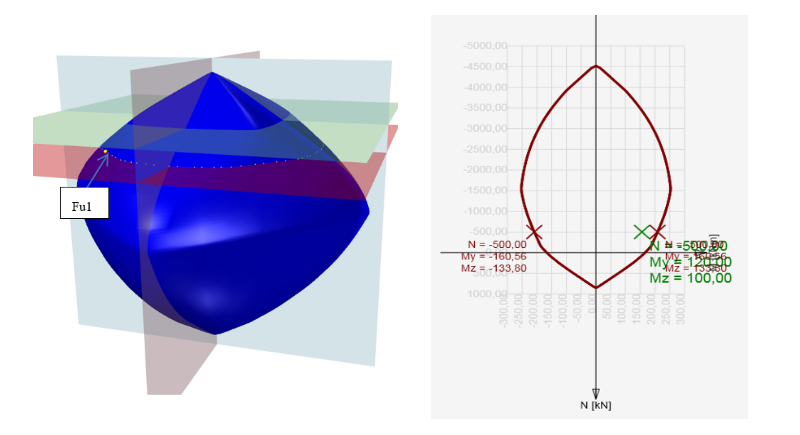
La primera opción es comprobar la sección transversal mediante una superficie de interacción (o diagrama de interacción). En la figura siguiente se ofrece una explicación sobre una muestra de las superficies de interacción para la sección cuadrada reforzada del ejemplo. En la superficie de interacción se sitúan los puntos que definen el estado límite último de la sección transversal examinada.La superficie de interacción se dibuja a partir de los puntos (N, My, Mz), que vienen determinados por la integración de tensiones en la sección transversal, que ha alcanzado la deformación límite última en uno de los materiales.Para una interacción 3D, la superficie puede derivarse de un diagrama de interacción 2D, que es una curva cerrada, que corresponde a la tensión de un eje neutro girado constantemente.

\Sección transversal reforzada simétrica.

\La superficie de interacción muestra las condiciones de fallo para todos los casos de carga de fuerza normal y momentos flectores.

Para el caso de una sección transversal simétrica alrededor del eje y, el diagrama de interacción es simétrico alrededor del plano _N-My. Del mismo modo, para el caso de una sección transversal simétrica alrededor del eje z, el diagrama de interacción es simétrico alrededor del plano _N-Mz. La sección reforzada unilateral introduce una forma aplanada del diagrama de interacción.

\[ \textsf{\textit{\footnotesize{\qquad Sección transversal reforzada simétrica unilateral.}}]

\Superficie de interacción para la sección transversal con refuerzo simétrico simple.

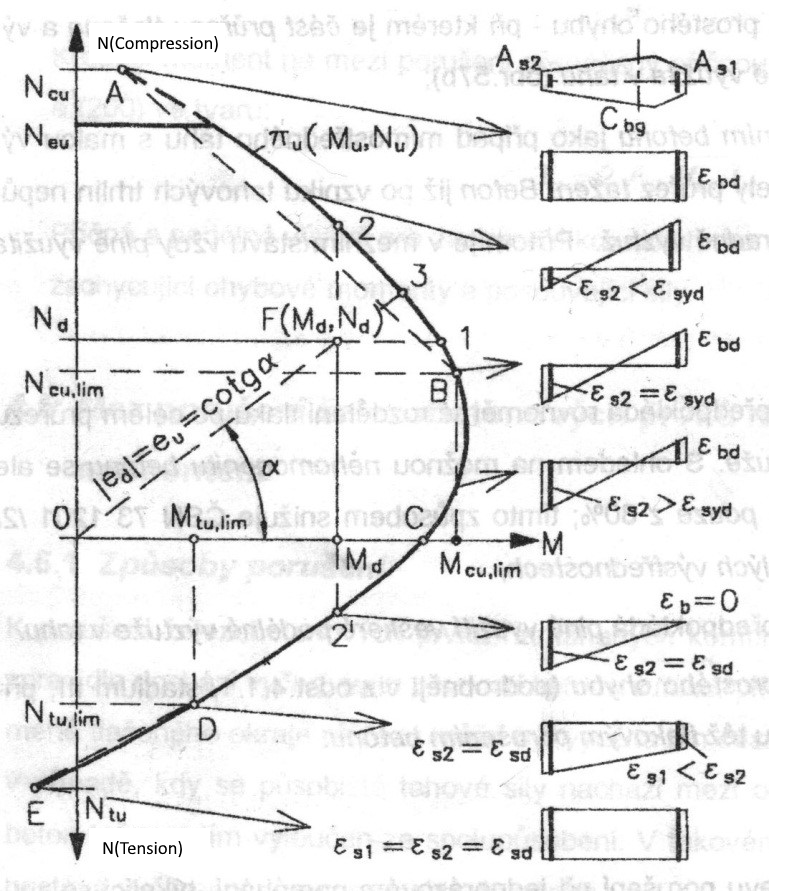
Los puntos que definen el estado límite último se obtienen de la integración de tensiones. La siguiente figura muestra la deformación en el estado límite último.

Distribuciones de deformación en el estado límite último (tomado de [2]).

El diagrama de interacción muestra el fallo de la sección transversal bajo fuerza normal y momentos flectores. [1]

Respetando el problema del diagrama 2D (curva cerrada situada sobre la superficie de interacción) podemos averiguar que el plano de deformación pasa por el eje neutro y el punto crítico [y, z, ε], que se considera como punto crítico R. El punto [y, z] define un punto de la sección transversal con el valor de deformación ε en el estado límite último. La inclinación del eje neutro es constante para todos los puntos del diagrama 2D.

En caso de que el esfuerzo de compresión en el hormigón sea crítico para el diseño, el punto R coincide con la fibra de hormigón más comprimida o con el punto límite C. Sin embargo, esto sólo puede aplicarse si esa sección está hecha de un tipo de hormigón, no como una sección transversal mixta.

En el caso de que la tensión de tracción en la armadura sea crítica para el cálculo (se supera la deformación _εud en el estado límite último para una o más barras), debe cumplirse la condición de que para el plano de deformación dado no se supere el valor _εud en ninguna otra barra.

\Utilización óptima del material de la sección transversal.

\Posiciones características del plano de deformación calculadas para el diagrama de interacción.

La imagen anterior muestra que el diagrama puede dividirse en dos partes: la parte en la que el fallo se produce por una fuerza de tracción y la parte que falla por una fuerza de compresión.Los puntos límite corresponden al caso anterior, donde también se aprecia la inclinación extrema del plano de deformación.Al dibujar un diagrama de interacción, la inclinación del plano de deformación de una sección transversal cambia en este intervalo, mientras buscamos el punto R (véase más arriba). Basándonos en ese plano definido realizamos la integración para obtener la tensión en el estado límite último.

Comprobación de la sección transversal sometida a un esfuerzo axil y a un momento flector

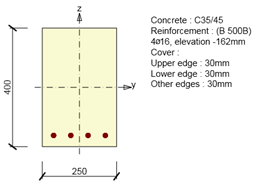
La comprobación de una sección sometida a un esfuerzo axil y a un momento flector se basa en probar que las tensiones comprobadas (combinación _Nd,_Myd, _Mzd) se encuentran dentro o en la zona de interacción superficial. El siguiente ejemplo muestra la comprobación de una sección rectangular sometida a fuerzas Nd₌ -500 kN,_Myd = 120 kNm, _Mzd = 100 kNm.

Método NuMuMu

Para definir la resistencia de una sección transversal suponemos cambios proporcionales en todos los componentes de la fuerza interna (la excentricidad de la fuerza normal permanece constante) hasta que se haya desarrollado la superficie interactiva.El cambio de las fuerzas internas implicadas puede interpretarse como un desplazamiento a lo largo de una líneaque une el sistema de coordenadas inicial (0,0,0) y el punto definido por las fuerzas internas (_NEd,_MEd,y,_MEd,z).Las dos intersecciones de esta línea con la superficie de interacción, que pueden encontrarse, representan dos conjuntos de fuerzas en el estado límite último. En cada intersección, el programa determina tres fuerzas en el estado límite: la resistencia de la fuerza axil de cálculo _NRd y los correspondientes momentos de resistencia de cálculo_MRdy,_MRdz.

Método NuMM

Para definir la resistencia de la sección transversal suponemos una fuerza normal constante (que es igual a la fuerza normal de cálculo actuante) y cambios proporcionales en los momentos flectores hasta que se haya desarrollado la superficie interactiva.El cambio de las fuerzas internas implicadas puede interpretarse como un desplazamiento en un plano horizontal a lo largo de la línea que une el punto (_NEd,0,0) y el punto definido por las fuerzas internas actuantes (_NEd,_MEd,y,_MEd,z).Las dos intersecciones de esta línea con la superficie de interacción, que puede encontrarse, representan dos conjuntos de fuerzas en el estado límite último. En cada intersección el programa determina tres fuerzas en el estado límite: los momentos resistentes de cálculo_MRdy,_MRdz y la (correspondiente) fuerza normal de cálculo actuante_NEd.

Método NMuMu

Para definir la resistencia de la sección transversal asumimos una fuerza normal constante (que es igual a la fuerza normal de cálculo actuante) y cambios proporcionales en los momentos flectores hasta que se haya desarrollado la superficie interactiva.El cambio de las fuerzas internas implicadas puede interpretarse como un desplazamiento en un plano horizontal a lo largo de la línea que une el punto (_NEd,0,0) y el punto definido por las fuerzas internas actuantes (_NEd,_MEd,y,_MEd,z).Las dos intersecciones de esta línea con la superficie de interacción, que pueden encontrarse, representan dos conjuntos de fuerzas en el estado límite último. En cada intersección, el programa determina tres fuerzas en el estado límite: los momentos resistentes de cálculo_MRdy,_MRdz, y la (correspondiente) fuerza normal de cálculo actuante_NEd.

Determinación de la respuesta de la sección

Otra posibilidad para comprobar la sección es hallar la respuesta de la sección (es decir, la distribución de deformaciones y tensiones a partir de las fuerzas internas actuantes). Este método también se conoce como método de deformación límite.El nivel de tensiones actuantes en cada fibra (en el caso de flexión plana en cada capa) encada barra reforzada se calcula en función de la deformación del diagrama Tensión-Deformación del material.
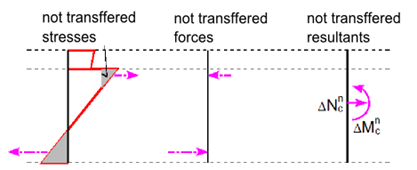
La respuesta de la sección transversal se calcula mediante el método numérico especificado en[6]. El principio consiste en el incremento gradual de la carga de la sección por las componentes desequilibradas de las fuerzas no transferidas. Éstas se obtienen integrando la tensión sobre la sección utilizando los diagramas Tensión-deformación.Si se puede encontrar el valor de la tensión para la deformación en el diagrama Tensión-Deformación, véase la figura siguiente (a), la tensión calculada es correcta suponiendo un material elástico lineal.En los casos (b) y(c), la tensión para un cálculo lineal alcanza valores irreales, y parte (b) o todo el valor (c) no pueden ser transmitidos por el material. Integrando las tensiones no transmitidas obtenemos las fuerzas internas no transmitidas, y sus resultantes deben sumarse a las fuerzas internas de las cargas variables.

Tensiones no transferidas en los diagramas Tensión-Deformación [4].

Fuerzas internas no transferidas.[4]

Este método de cálculo requiere el uso de métodos numéricos para integrar la tensión sobre el área de la sección transversal y para el análisis no lineal de las ecuaciones de equilibrio en la sección. La iteración finaliza cuando se cumplen los criterios de convergencia.

\[\frac{{F_e}} - {F_i}}{{{F_e}} \le max\left\{ {e,d} \right\}].

donde

_{Fe es la} carga de sección,

_{Fi es} la respuesta de la sección (fuerzas internas calculadas en la base del plano de deformación).

Si a es el valor aproximado (aproximado) y b es el valor exacto (verdadero), la desviación absoluta viene dada por la siguiente ecuación.

\[e = \left| {b - a} \right||]

La desviación relativa viene dada por la siguiente fórmula:

\[d = \left| {\frac{{b - a}}{b}} \right|\\]

En la mayoría de los programas, puede establecer estos criterios de convergencia (los valores por defecto son 1%como error relativo, 100 N, 100 Nm como error absoluto de la fuerza normal y momentos).

Así que si tenemos la entrada de N = 0 kN, My = 100 kNm, Mz= 0 kNm y las fuerzas integradas después de la iteración N = - 0.07 kN, My = 100,5 kNm, Mz = 0,02 kNm, la evaluación será la siguiente. Respetando que N y Mz sean iguales a 0, se puede hacer una comparación con desviación absoluta:

El valor de la fuerza normal 100N> | 70 | N
El valor del momento flector Mz 100Nm> | 20 | Nm
El valor del momento flector My

\[d = \left| {\frac{{b - a}}{b}} \right| = \frac{100 - 100,5}{100}} = 0,005\; < 0,01\]

Comprobación transversal por la respuesta

En el caso de encontrar un equilibrio en la sección transversal, se conoce la deformación plana.A partir de la deformación plana, podemos calcular la deformación en cualquier punto de la sección y, a continuación, la tensión o las fuerzas internas en las barras de refuerzo, la sección transversal o sus partes utilizando los diagramas de tensión-deformación de los materiales. Los valores calculados de tensión y deformación se comparan con el valor límite de deformación de los diagramas de tensión-deformación de los materiales utilizados.
La ventaja de este método es que obtenemos una imagen completa de los valores de tensión y deformación en la sección de las fuerzas internas que actúan sobre la sección transversal.

Cizalla

Con respecto al fallo por fragilidad, la comprobación del esfuerzo cortante es una de las comprobaciones importantes de una sección de hormigón armado.

Procedimiento de cálculo

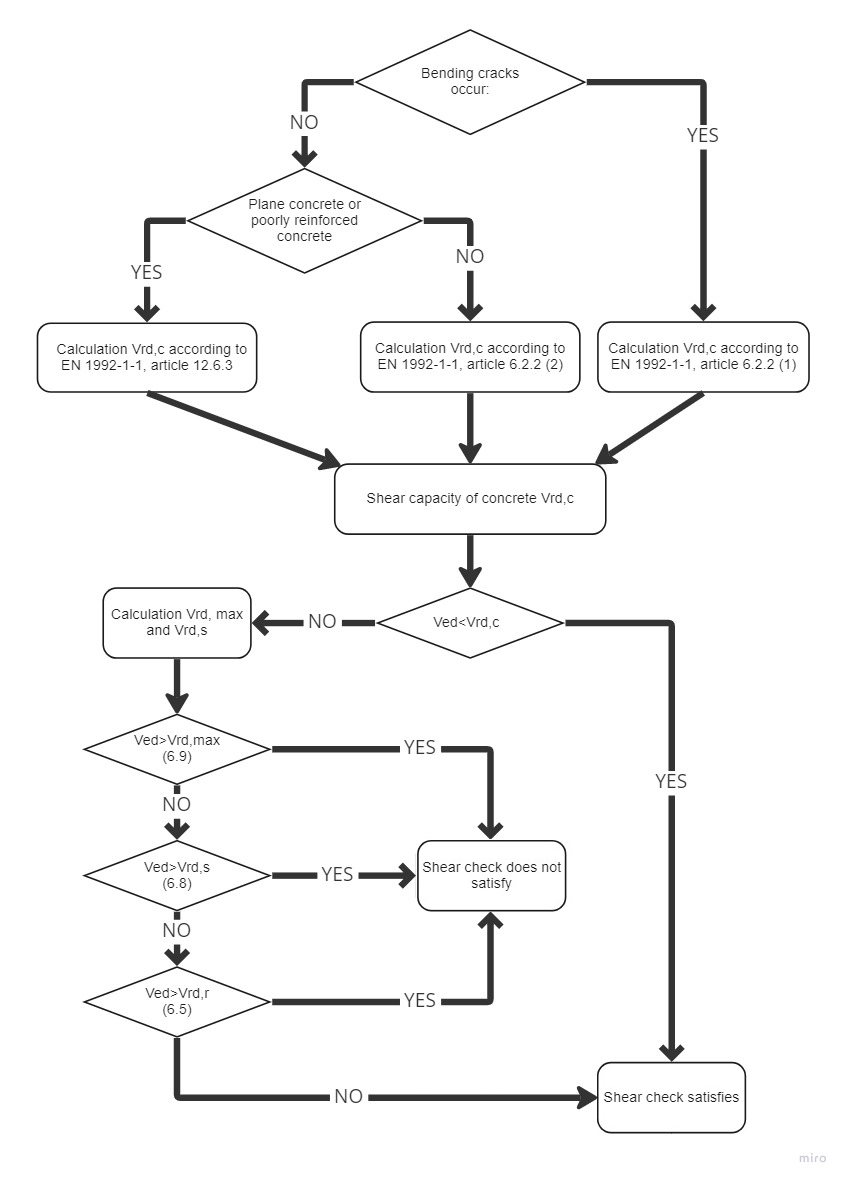
El cálculo de la resistencia a cortante se compone de varias partes básicas. En primer lugar se debe analizar si se producen o no fisuras por flexión en el lugar comprobado.Si las hay, se utiliza el cálculo según la norma EN 1992-1-1[2], artículo 6.2.2 (1).En caso contrario, determinamos si se trata de hormigón plano o poco armado, y procedemos según la norma EN 1992-1-1, artículo 12.6.3.

Para el hormigón armado no fisurado (sin armadura de cortante) comprobamos según EN 1992-1-1 Artículo 6.2. (2).En el caso de elementos que requieran armadura de cortante, se comprobará de acuerdo con el artículo 6.2.3[2].

\Diagrama de proceso para la comprobación a cortante.

Resistencia a cortante de elementos sin refuerzo a cortante

Resistencia a cortante de elementos en zonas de flexión fisurada (art. 6.2.2 (1)[2])

La resistencia a cortante de elementos de hormigón armado sin armadura de cortante sometidos a momento flector viene dada por:

\[{{V}_{Rd,cm}}=~{{C}_{Rd.c}}k~{{\left( 100~{{\varrho }_{l}}{{f}_{ck}} \right)}^{{}^{1}/{}_{3}}}~{{b}_{w}}d\]

Que se definió a partir de los ensayos realizados en un número representativo de vigas simples en caso de fallo por esfuerzo cortante. Dado que la resistencia anterior puede ser cero para los elementos sin refuerzo longitudinal (_rl), para los miembros poco reforzados se derivaron ecuaciones. Dado que la resistencia anterior puede ser cero para los elementos sin refuerzo longitudinal (_rl), para los miembros mal reforzados se determinó mediante la ecuación

\[{{V}_{Rd,c}}ge ~{{{upsilon }_{min}}{{b}_{w}}d\]]

Para la resistencia a cortante con influencia de la fuerza normal se determinó mediante la ecuación

\[{{V}_{Rd,cn}}=~{{k}_{1}}{{\sigma }_{cp}}~{{b}_{w}}d\]

Resistencia al cizallamiento en su expresión completa que se corresponde con EN 1992-1-1 art. 6.2.2 (1)

\[{{V}_{Rd,c}}=~{left[ {{C}_{Rd.c}}k~{{left( 100~{{varrho }_{l}}{{f}{ck}} \right)}^{{}^{1}/{}_{3}}+{{{k}_{1}{{sigma }_{cp}}{right} \...]~{b}_{w}d]

Con un mínimo de

\{{V}_{Rd,c}}=~\left( {{\upsilon }_{min}}+{{k}_{1}}{{sigma }_{cp}} {right){{b_{w}d]

donde

_CRd,c = 0,18 / _γc,

k factor de altura de la sección transversal

\[k=1+\sqrt{\frac{200}{d}}<2,0\]

_ρ1 coeficiente de refuerzo de la armadura longitudinal

\[{{\varrho }_{l}}=\frac{{{A}_{sl}}}{{{b}}d}}le 0,02\]

_fck resistencia cilíndrica a la compresión característica del hormigón a 28 días

_k1 = 0,15

_σcp =_NEd /_Ac < 0,2 _fcd v MPa

_bw anchura mínima de la sección transversal en la zona de tracción

d profundidad efectiva de una sección transversal

_υmin resistencia mínima al cizallamiento equivalente _υmin = 0,035 ^{k3/2 fck1/2}

Resistencia a cortante de los elementos en zonas de flexión no fisuradas (art. 6.2.2 (2)[2])

La resistencia a cortante de los elementos en zonas de flexión no fisuradas puede determinarse a partir del círculo de Mohr. En la ecuación

\[{{sigma }_{1,2}}=\frac{{{sigma }__{x}}+{{sigma }_{y}}{2}pm \sqrt{{{left( \frac{{sigma }_{x}}-{{sigma }__y}}{2}{right)}^{2}}+\tau _{z}^{2}}].

Sustituimos _σx = _σcp a τz_{= VRd,c} S / (I _bw) y calculamos_VRd,c y obtenemos la ecuación correspondiente con la fórmula dada en EN 1992-1-1 art. 6.2.2 (2)

donde

I es el segundo momento del área,

_bw es la anchura de la sección transversal en el eje centroidal

S es el primer momento del área por encima y alrededor del eje centroidal,

_fctd resistencia a la tracción axial de diseño del hormigón en MPa,

_scp es el esfuerzo de compresión del hormigón en el eje centroidal debido a la carga y/o al pretensado,

_al factor de longitud de transmisión, normalmente 1,0.

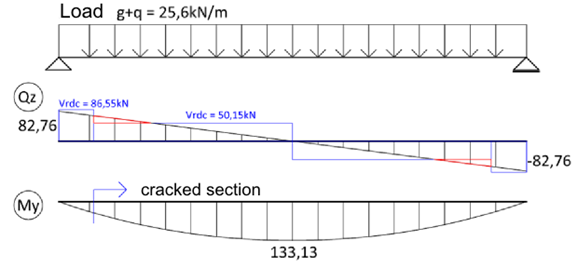
En relación con lo anterior, debe tenerse en cuenta que en zonas sin fisuras por flexión laresistencia_{VRd ,c} puede ser significativamente mayor que en las zonas agrietadas según el artículo 6.2.2 (1)[2]. La figura siguiente muestra claramente que aunque el esfuerzo cortante se verifique en su extremo (que no produce fisuras), no tiene por qué garantizar que se transmita a lo largo de toda la longitud de la viga.Esto se debe a un cambio en el método de cálculo de la resistencia al cizallamiento del hormigón.Por supuesto, la resistencia al cizallamiento puede considerarse según el artículo 6.2.2 (1)[2] también en lugares donde no se producirán fisuras.

\Comparación de la resistencia al corte antes y después de la aparición de grietas.

A la expresión de_{VRd, c} según el artículo 6.2.2 (2)[2] también debe tenerse en cuenta que en el caso general debe basarse en la comprobación en la fibradel esfuerzo de tracción principal extremo del hormigón en la zona del esfuerzo de compresión normal, pero no en el centro de gravedad de la sección.En este punto es necesario calcular las características de la sección transversal (S y _bW).Para determinar la tensión principal máxima _s1 en el programa IDEA RCS trazamos una línea a través del centro de gravedad en la dirección de los esfuerzos cortantes resultantes.Esta línea la dividimos en 20 sectores. En esta línea presentaremos más puntos característicos (puntos del polígono de la sección transversal, centro de gravedad, el eje neutro).Dentro de estos puntos, calculamos S, _bw, _σx, _τyz a σ1_. En el punto de máxima tensión principal de tracción calcularemos la resistencia al cizallamiento.

El esfuerzo cortante antes de aplicar el factor de reducción b exigido por el artículo 6.2.2 (6) debe cumplir la condición adicional

\[ {{V}_{Ed}}le 0,5~{{b}_{w}}d~\upsilon ~{{f}_{cd}}]

donde

\ [ {{ υ}}\le 0,6\left[ 1-\frac{{f}_{ck}}}{250} \right]\] kde _fck je v MPa

Resistencia a cortante de elementos sin armadura o ligeramente armados (art. 12.6.3[2])

La resistencia a cortante para hormigón liso o ligeramente armado puede determinarse a partir de la expresión

\[ {{\tau }_{cp}}le k~{{V}_{Ed~}}/{{A}_{cc}}]

Donde

_τcp lo sustituimos por

\[ {{f}_{cvd}}={sqrt{f_{ctd,pl}^{2}+{{\sigma }_{cp}}{f}_{ctd,pl}}~pro~{{sigma }_{cp}}le {{sigma }_{c,lim}}~]

o

\{ {{f}_{cvd}={sqrt{f_{ctd,pl}^{2}+{{{sigma }_{cp}}{f}_{ctd,pl}}-{left( {frac{{sigma }_{cp}}-{{{sigma }_c,lim}}{2}{right)}^2}}~{pro~{{sigma }_{cp}}>{{{sigma }_{c,lim}}~]

Los valores parciales utilizados en la fórmula anterior vienen dados por:

\{{{sigma }_{c,lim}}={{f}_{cd,pl}}-2{sqrt{{{f}_{ctd,pl}}left( {{f}_{ctd,pl}}+{{f}_{cd,pl}} \right)}}.

donde

fcd_,pl Resistencia a compresión de diseño para hormigón simple o poco armado,

fctd_,pl Resistencia a la tracción axial calculada para hormigón simple o poco armado,

_fcvd Resistencia de cálculo a cortante bajo compresión del hormigón.

Resistencia de elementos con armadura de cortante (art. 6.2.3[2])

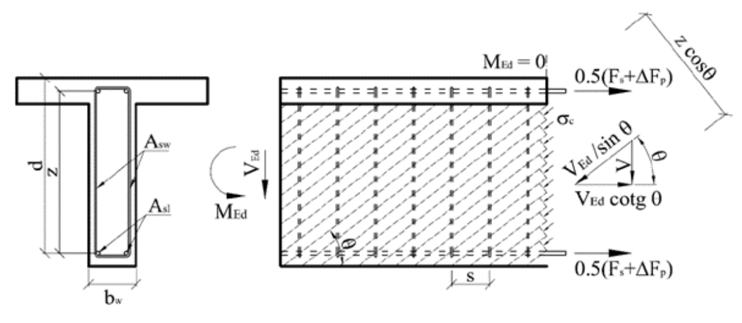
El cálculo de la resistencia de elementos de hormigón armado con armadura de cortante se basa en el método de analogía de celosía con diagonales de ángulo variable.La base de este método es el equilibrio de fuerzas en el triángulo determinado por la fuerza del puntal (diagonal), la fuerza de la armadura de cortante (estribo) y la fuerza de la armadura longitudinal.

\[ \textsf{\textit{\footnotesize{qquad Principio de la analogía de Truss para miembro bajo carga de cortante.}}]

La sección transversal bajo carga de corte se rompe por las grietas en un ángulo θ, por esta razón la diagonal de hormigón con el mismo ángulo que las fuerzas de corte está resistiendo a la fuerza de corte. La fuerza de compresión de la diagonal se puede expresar como _Ved/sinθ. Esta fuerza debe ser transferida por la superficie del hormigón, perpendicular a la diagonal de compresión _bwzcosθ. El esfuerzo de tensión del hormigón en la diagonal de compresión es entonces igual:

\[ {{sigma }_{c}}={frac{{V}_{Ed}}{{b}{w}}z~sin \text{ }!\!\theta!\text{ }cos \theta }={frac{{V}_{Ed}}{{b}{w}}z}left( \tan \theta +\cot \theta \right)\}].

Sustituyendo "sigma" por "alfa" y " V"... y expresando \ [{{V}_{Rd,max}} obtenemos la ecuación para la resistencia al corte de la diagonal:

\[ {{V}_{Rd,max}}=~{\\alpha }_{cw}}~{{b}_{w}}~z~{{\nu }_{1}}{{f}{cd}}/left( \cot \theta +\tan \theta right)\}]

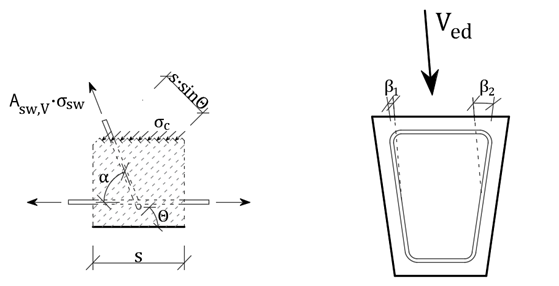
Para equilibrar el componente de fuerza vertical en la diagonal de compresión, se utilizará un refuerzo de cortante.El tamaño de la fuerza vertical se basa en la tensión de compresión diagonal en elEl tamaño de la fuerza vertical se basa en la tensión de compresión diagonal en el área del hormigón que corresponde a un estribo - \ [{{sigma }_{c}}{{b}}_{w}}s{{sin }^{2}}\theta\]. La fuerza límite del estribo viene dada por \ [{{A}_{sw}}{{f}_{ywd}}/s].

Insertando _σc, comparando con la fuerza límite en la armadura, tras las modificaciones obtenemos:

\[ \frac{{{A}_{sw}}{{f}_{ywd}}}{s}=\frac{{{V}_{Ed}}}{z}\tan \theta\]

Entonces expresando _Ved como_VRDs obtenemos la resistencia de la sección transversal con refuerzo de cortante vertical:

\[ {{V}_{Rd,s}}=~\frac{{{A}_{sw}}}{s}z~{{f}_{ywd}}\cot \theta\]

El esfuerzo cortante longitudinal es transferido por la armadura longitudinal y puede determinarse como _Vedcotgθ. La derivación de las fórmulas anteriores puede encontrarse en[4].

Utilizando el programa IDEA RCS es posible comprobar sólo las barras con armadura de cortante vertical. En general se pueden utilizar las siguientes ecuaciones:

\[{{V}_{Rd,s}}=~\frac{{{A}_{sw}}}s}z~{{f}_{ywd}}left( \cot \theta +\cot \alpha \right)\sin \alpha]].

\{{V}_{Rd,max}}=~{\\alpha }_{cw}}~{{b}_{w}}~z~{{\nu }_1}}{{f}{cd}}left( \cot \theta +\cot \alpha \right)/\left( 1+{\cot }^{2}}\theta \right)\}

Donde

_Asw es el área transversal de la armadura de cortante,

s es la separación de los estribos,

_fywd es el límite elástico de diseño del refuerzo para esfuerzo cortante,

_bw es la anchura mínima entre los cordones de tracción y compresión. Para calcular la resistencia_VRd,max , el valor de la anchura de la sección debe reducirse a la denominada anchura nominal de la sección transversal en caso de que la sección transversal esté debilitada por conductos de cables

bw_,nom=bw-0,5ΣΦ para conductos metálicos rejuntados

bw_,nom=bw-1,2ΣΦ para conductos metálicos sin rejuntado

υ = 0,6 pro _fck ≤ 60MPa o pro _fck > 60MPa,

_αcw es un coeficiente que tiene en cuenta el estado de la tensión en el cordón de compresión.

Carga	σcp = 0	0 <σcp≤0,25fcd	0,25fcd <σcp≤0,5fcd	0,5fcd <σcp≤1,0fcd
Coeficienteacw	1,0	1+σcp/fcd	1,25	2,5(1 - σcp/fcd)

Tab. 1-1 Coeficiente determinante _αcw

El ángulo θ es el ángulo entre el puntal de compresión del hormigón y el eje de la viga perpendicular al esfuerzo cortante. Los valores límite de cotθ para su uso en un País pueden encontrarse en su Anexo Nacional. Los límites recomendados vienen dados por la expresión

\[1~\le ~\cot \theta \le 2,5\]

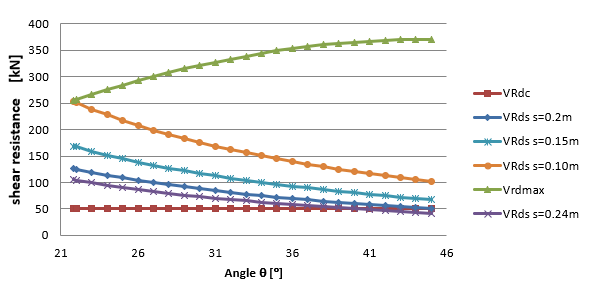
14. La elección del tamaño del ángulo θ puede afectar al valor de las resistencias. La dependencia de las resistencias es visible en la figura 1.15. La figura muestra que con el aumento del ángulo θ la resistencia_VRd,max aumenta, y la resistencia_VRd,s disminuye. La resistencia_VRd,c es constante, ya que se basa en el método de analogía de cerchas.

\[ \textsf{\textit{\footnotesize{\qquad Dependencia entre la resistencia a cortante y el ángulo q.}}]

Cálculo de las características de la sección transversal a cortante

Para calcular el cortante es importante calcular las variables de la sección transversal que afectan a la resistencia al cortante.Estas variables incluyen principalmente la anchura de la sección resistente a cortante _bw, la profundidad efectiva d y el brazo de palanca z. El código[2] proporciona estos valores que se correlacionan directamente con el esfuerzo de flexión real.Pero el problema es determinar estos valores cuando la dirección de los momentos flectores resultantes (o más exactamentela dirección de la resultante de la resistencia de la sección) es significativamente diferente de la dirección de los esfuerzos cortantes resultantes.En este caso, el código EC2 no proporciona ninguna recomendación.

Anchura de la sección resistente a cortante _bw

El programa IDEA RCS calcula la anchura de la sección transversal resistente a cortante en la dirección perpendicular a la resultante de los esfuerzos cortantes.Dependiendo del artículo del Eurocódigo, esta anchura se calcula como:
- La menor anchura de la sección entre la resultante del hormigón a compresión y la armadura a tracción en la dirección perpendicular a la resultante de los esfuerzos cortantes para el artículo 6.2.2 (a) y 6.2.3 (1)
- La anchura de la sección en dirección perpendicular a la resultante de los esfuerzos cortantes en el punto comprobado según el artículo 6.2.2 (2)

Profundidad efectiva de una sección transversal

La profundidad efectiva suele definirse como la distancia de la fibra de hormigón más comprimida al centro de gravedad de la armadura.Dado que está directamente relacionada con la flexión, la distancia se da como proyección perpendicular a la línea de gravedad de la deformación plana.

Esta definición puede aclararse de modo que en lugar del centro de gravedad de la armadura de tracción se utilice la posición de la resultante de fuerzas de la armadura.Durante el desarrollo del programa IDEA RCS se resolvió el problema decómo definir la profundidad efectiva de la sección transversal, para la que el plano de cargas de flexión no se corresponde con la dirección de las fuerzas resultantes de cizallamiento.Por lo tanto, la profundidad efectiva se define como la distancia de la fibra de hormigón más comprimida a las fuerzas resultantesen la armadura de tracción (en función del esfuerzo de flexión) y en la dirección de los esfuerzos cortantes resultantes, véase la figura 1.17.

Se producirán casos excepcionales si no podemos determinar la fibra comprimida o la resultante en la armadura de tracción. En este caso, recomendamos utilizar el valor 0.9 h (90% de la profundidad de la sección en la dirección de los esfuerzos cortantes resultantes). Este valor, el usuario puede definirlo en el programa IDEA RCS mediante el ajuste de variables de código.

Brazo de palanca de los esfuerzos internos

El brazo de palanca de los esfuerzos internos se encuentra en 6.2.3 (3)[2] y se define como la "distancia entre las cuerdas de tracción y compresión". El código no define cómo proceder cuando el plano del momento flector actuante es diferente de la dirección de los esfuerzos cortantes resultantes.Por lo tanto, como en el caso de la profundidad efectiva, definimos la distancia en la dirección de los esfuerzos cortantes resultantes.También aquí, podemos enfrentarnos a casos de excepción similares, por ejemplo, toda la sección está bajo compresión, etc. En este caso, tomamos el valor 0.9 d (90% de la altura efectiva de la sección). Este valor, el usuario puede establecerlo en el programa IDEA RCS mediante el ajuste de variables de código.

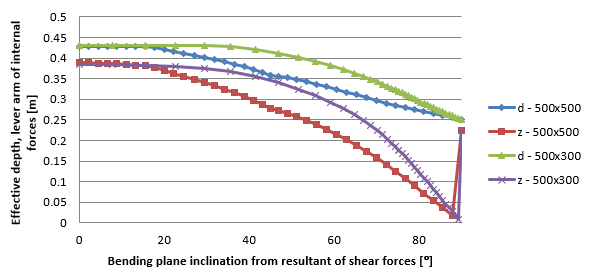
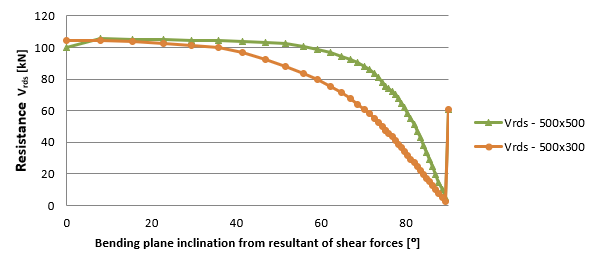
La dependencia entre la inclinación del plano de flexión y la resultante de la fuerza cortante es claramente visible en la Figura 1.18 y la Figura 1.19. Con un aumento de la inclinación del plano de flexión, la resultante de la fuerza cortante es mayor.19. Con un aumento de la inclinación, los valores de la altura efectiva, los brazos de palanca y las resistencias relacionadas disminuyen. El estado límite es 90°. Para esta inclinación no se puede calcular el brazo de palanca de las fuerzas internas, por lo que el brazo de palanca es igual a cero. En este caso, se considera el valor especificado en el ajuste de las variables del código. Este estudio demuestra que el máximo recomendado para la inclinación es de unos 20°.

\[ \textsf{\textit{\footnotesize{qquad Dependencia entre la profundidad efectiva, el brazo de palanca a la inclinación del plano de flexión y la resultante de los esfuerzos cortantes.]

\Dependencia entre la resistencia Vrds a la inclinación del plano de flexión y la resultante de los esfuerzos cortantes.

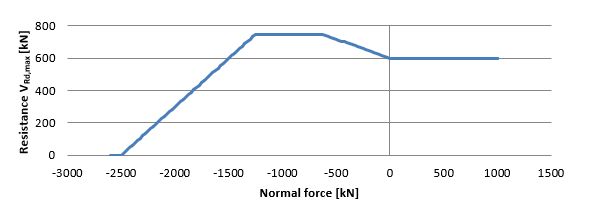
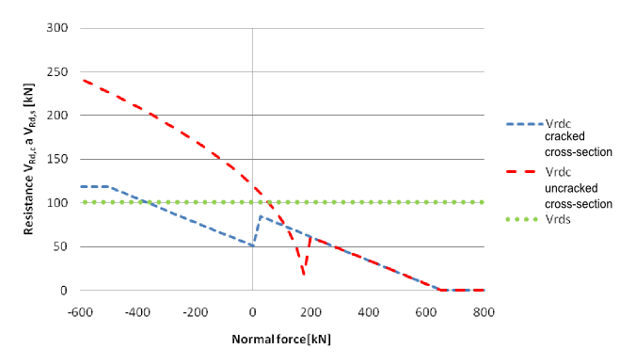
Como parte de las pruebas de la aplicación RCS, se realizó un estudio sobre la dependencia de la resistencia al cizallamiento al cambio de la fuerza normal. La resistencia_VRd,max sólo se ve afectada por el coeficiente _αcw, ver Fig. 1.20. La Fig. 1.21 muestra un valor constante de la resistencia_VRds. Para la resistencia_VRdc, las disminuciones causan el aumento de la fuerza normal.La curva azul de la Fig. 1.21 muestra la resistencia_VRdc despreciando la influencia de las grietas y se calculó utilizando la fórmula de la sección 6.2.2 (1)[2]. El salto en la transición entre presión y tensión es causado por el refuerzo de tracción aportado. La curva roja se calcula utilizando la fórmula del apartado 6.2.2 (2)[2]. Después de producirse la primera fisura, la curva de dependencia es la misma que la del apartado 6.2.2 (1)[2].

\Curva de dependencia de la resistencia a cortante VRd,max a la fuerza normal.

\Dependencia de las resistencias al corte VRd,c y VRd,s con la fuerza normal.

Torsión

Hipótesis de cálculo

El comportamiento de una sección de hormigón armado sometida a torsión puede dividirse en dos categorías: antes y después del momento en que cabe esperar que se produzcan las primeras fisuras. Antes de la fisuración, la sección se comporta como un material elástico. El esfuerzo de torsión puede expresarse mediante la fórmula

\[\tau =~\frac{{{T}_{Ed}}}{{{W}_{t}}}\]

donde _Wt je módulo seccional en torsión.

Las fisuras en el miembro no reforzado debidas al esfuerzo principal de torsión son también estados límite últimos. El comportamiento de una sección de hormigón armado sometida a torsión puede describirse a partir de una sección cerrada de pared delgada, véase la Fig. siguiente.

\Sección transversal de pared delgada equivalente.

Procedimiento de cálculo

El proceso de comprobación del hormigón armado a torsión es muy similar al de comprobación a cortante. En primer lugar, se comprueba la resistencia del hormigón.Si la comprobación del hormigón se cumple, la armadura puede diseñarse utilizando las reglas de detalle. En caso contrario, necesitamos comprobar la armadura y la resistencia diagonal a compresión mediante cálculo.

\Diagrama de proceso para la comprobación de torsión.

Resistencia

El flujo cortante en una pared de sección delgada sometida a torsión puede expresarse como:

\[ {{\tau }_{t}}{{t}_{ef}}=~\frac{{{T}_{Ed}}}{2{{A}_{k}}]

La fuerza cortante en una pared de una sección transversal de pared delgada puede expresarse como:

\[ V={\tau }_{t}}{{t}_{ef}}z]

Donde

τ Flujo cortante en la pared,

_tef es el espesor efectivo de la pared,

z es la longitud lateral de la pared,

_TEd es el momento de torsión,

_Ak es el área encerrada por las líneas centrales de las paredes de conexión, incluyendo las áreas huecas interiores.

El momento de torsión, que puede determinarse ajustando _fctd a la expresión anterior. Así obtenemos la expresión para la resistencia en torsión sin refuerzo de torsión.

\[ {{T}_{Rd,c}}=2{{A}_{k}}{{t}_{ef}}{{f}_{ctd}}\]

donde _fctd resistencia a tracción axial de diseño del hormigón

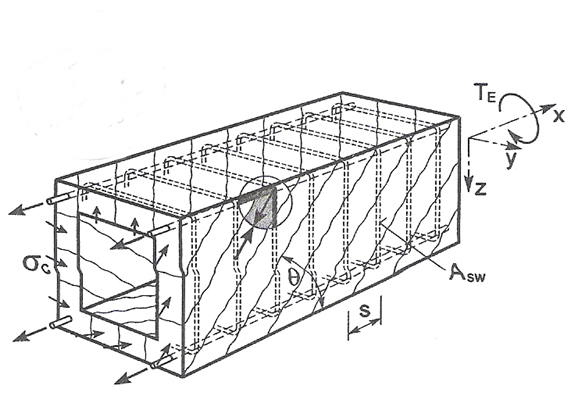
\[ \textsf{\textit{\footnotesize{\qquad Principios de la analogía de la cercha para el miembro bajo momento de torsión.}}]

La resistencia del elemento con refuerzo de torsión se compone a partir de la resistencia a compresión de las diagonales de hormigón, que se basa de nuevo en el método de analogía de celosía. El esfuerzo de compresión en la diagonal se puede expresar con la ayuda del esfuerzo cortante en la pared de una sección transversal de pared delgada en la superficie de la pared que se está considerando, es decir

\[{{sigma }_{c}}={frac{\frac{{T}_{Ed}}z}{2{{A}_{k}}sin \theta }}{z~{t}_{ef}}cos \theta }={frac{{T}_{Ed}}{2{{A}_{k}}{t}_{ef}}sin \theta \cos \theta }].

Sustituyendo _σc=σcwfcd y_TEd=TRd,max y expresando_TRd,max obtenemos una ecuación para la resistencia diagonal a compresión

\[{{T}_{Rd,max}}=2~\nu ~{{\alpha }_{cw}}~{{f}_{cd}}~{A}_{k}~{t}_{ef~\sin \theta ~cos \theta }]

donde

ν = 0,6 pro _fck ≤ 60MPa o para _fck > 60MPa

Coeficiente _αcw que tiene en cuenta el estado del esfuerzo de compresión en el cordón de compresión

_fcd valor de cálculo de la resistencia a compresión del hormigón

la resistencia de la armadura de cortante sometida a torsión se basa de nuevo en el esfuerzo en la diagonal de compresión. La fuerza de estribo es igual a la tensión en la diagonal de compresión en el área que corresponde a la línea de estribo particular, es decir

\[{{A}_{sw}}{{f}_{ywd}}={frac{{T}_{Ed}}{2{{A}_{k}}{t}_{ef}}sin \theta \cos \theta }~{t}_{ef}}~{sin }^{2} {theta ={frac{{T}_{Ed}}{s}2{{A}_{k}}cot \theta }~].

Sustituyendo_TEd=TRd,s y expresando_TRd, s obtenemos la ecuación:

\[{{T}_{Rd,s}}=2{{A}_{k}}\frac{{{A}_{sw}}{{f}_{ywd}}}{s}~\cot \theta\]

Si se conoce la cantidad de armadura longitudinal y de cortante, podemos definir el ángulo θ mediante la expresión

\[{{\tan }^{2}}\theta =\frac{\frac{{{A}_{sw}}{{f}_{ywd}}}{s}}{\frac{{{A}_{sl}}{{f}_{yd}}}{{{u}_{k}}}}\]

Sustituyendo_TRd,s obtenemos

\[{{T}_{Rd,s}}=2{{A}_{k}}\sqrt{\frac{{{A}_{sw}}}{s}{{f}_{ywd~}}\frac{{{A}_{sl}}}{{{u}_{k}}}~{{f}_{yd}}}\]

Donde

_Asw área de refuerzo para esfuerzo cortante

s es la separación radial de los estribos del refuerzo para esfuerzo cortante

_fywd es la resistencia efectiva de diseño del refuerzo para esfuerzo cortante

_Asl área de refuerzo longitudinal

_uk es la circunferencia exterior de la sección transversal

_fywd es la resistencia efectiva de cálculo de la armadura longitudinal

La fuerza en la armadura longitudinal puede deducirse de La fuerza cortante en un muro de una sección sometida a un momento torsor puro, que se da como:

\[V=\frac{{{T}_{Ed}}}{2{{A}_{k}}}{{u}_{k}}\]

Esa fuerza se transforma a la dirección longitudinal y obtenemos:

\[{{F}_{l}}=\frac{{{T}_{Ed}}{{u}_{k}}}{2{{A}_{k}}~\tan \theta }\]

El intervalo permitido de los valores del ángulo θ es similar al del control de cizalladura, es decir, 1 < cot θ < 2,5. La dependencia entre resistencias puede verse en la Fig. siguiente. El diagrama muestra que al aumentar el ángulo θ la resistencia_TRd,max es creciente, la resistencia_TRd.s es decreciente y la resistencia_TRd,c es constante, ya que no se basa en el método de analogía de cerchas.

\[ \textsf{\textit{\footnotesize{qquad Závislost únosnosti průřezu v kroucení na úhlu θ.}}]

Cálculo de las características de la sección transversal para la torsión

Para comprobar la sección transversal para la torsión es necesario establecer una denominada sección cerrada de pared delgada equivalente. En la determinación de las dimensiones de la sección transversal de pared delgada equivalente suponiendo una forma rectangular.Para el área real de los estados rectangulares A = b×h y para la circunferencia del rectángulo u =2 (b +h).El uso de estas dos ecuaciones puede proporcionar alternativa área de forma rectangular delgada y la periferia de la sección transversal original. Resolver dos ecuaciones con dos incógnitas que obtenemos:

\[b=\frac{-u\pm \sqrt{{{u}^{2}}-16A}}{-4}\text{ }\!\!~\!\!\text{ }]

\[h=\frac {\left( u-2\text{b} \right)}{2}]

El espesor de pared de la sección transversal efectiva puede definirse a partir de la periferia y el área de la sección como:

\[t=\text{A}/\text{u}\]

A continuación, el área y la periferia definida por la línea central de la sección transversal efectiva:

\[{A}_{k}=left( \text{h}-\text{t} \right)\text{ }\!\!~\!\!\text{ }left( \text{b}-\text{t} \right)\text{ }\!\!~\!\!\text{ }]

\[{{u}_{k}}=2\left( \left( \text{h}-\text{t} \right)+\text{ }\!\!~\!\!\text{ }\left( \text{b}-\text{t} \right) \right)\]

El problema con este método es para la sección transversal de tipo T con una placa ancha cuando se toma el área total y la periferia para calcular las dimensiones (incluyendo esta placa).En las futuras versiones del programa IDEA RCS se habilitará la selección de la parte de la sección transversal más maciza, que se utilizará para comprobar la torsión.

Interacción

Interacción de la fuerza cortante y la torsión para el refuerzo cortante

Determinación de la fuerza en la armadura de cortante debida al esfuerzo cortante.

El cálculo se basa en la fórmula para calcular la resistencia de la armadura de cortante definida en la norma EN 1992-1-1. Basado en la ecuación 6.13 (cap. 6.2.3 (4)), la resistencia a la carga de un estribo puede obtenerse como:

\[{{V}_{Rd,s}}=\frac{{{A}_{sw,V}}}{s}z{{f}_{ywd}}left( \cot \theta +\cot \alpha \right)\sin \alpha \cos \beta \].

\[\frac{{{A}_{sw,V}}}{s}={{a}_{sw,V}}\]

_Asw,V. . . área de la sección transversal de un estribo que resiste el cizallamiento en la sección considerada

s . . . . . espaciado del refuerzo para esfuerzo cortante en la dirección del eje longitudinal del elemento

_asw,V. . . área de la sección transversal del refuerzo para esfuerzo cortante por unidad de longitud

z . . . . el brazo de palanca interior. Para un elemento de canto constante, correspondiente al momento flector en el elemento considerado. En el análisis a cortante del hormigón armado sin esfuerzo axil, puede utilizarse normalmente el valor aproximado z = 0,9d.

_fywd. . . el límite elástico de cálculo de la armadura de cortante

θ . . . . el ángulo entre el puntal de compresión del hormigón y el eje del elemento perpendicular al esfuerzo cortante

α . . . . . ángulo entre la armadura de cortante y el eje del elemento perpendicular al esfuerzo cortante

β . . . . inclinación de la pata del estribo respecto a la resultante de la fuerza cortante aplicada

La fuerza cortante se redistribuye uniformemente entre las armaduras individuales que resisten la fuerza cortante en función del ángulo de la armadura y de la rigidez axial de las patas individuales del estribo.

\[{{V}_{ed}}={{V}_{ed,1}}+{{V}_{ed,2}}+...+{{V}_{ed,n}}\]

\[{{V}_{ed}={{varepsilon }_{sw,V}}\cdot z\cdot \sum\limits_{i=1}^{{n}_{V}}{{a}_{sw,i,V}}\cdot {{E}_{sw,i,V} {\cdot \left( \cot \theta + {\cot {{alpha }_{i}} \right)\cdot {{cos }^{2}} {{beta }_{i}}]

Además, se puede deducir la deformación media de la armadura considerada en la dirección del esfuerzo cortante resultante:

\[{{\varepsilon }_{sw,V}}=\frac{{{V}_{ed}}}{z\cdot \sum\limits_{i=1}^{{{n}_{V}}}{{{a}_{sw,i,V}}\cdot {{E}_{sw,i,V} {\cdot \left( \cot \theta + {\cot {{alpha }_{i}} \right)\cdot {{cos }^{2}}{{\beta }_i}}}}]

La deformación real de la i-ésima armadura puede calcularse como:

\[{{{varepsilon }_{sw,i,V}}=\frac{{{varepsilon }_{sw,V}} {{sin {{alpha }_{i}}}\cdot \cos {{beta }_{i}}].

La tensión en un tramo dado de la armadura:

\[{{sigma }_{sw,i,V}}= {{varepsilon }_{sw,i,V}}\cdot {{E}_{si,V}}]

Determinación de la fuerza en el estribo individual debida a la torsión

La resistencia a la torsión de una sección puede calcularse a partir de una sección cerrada de pared delgada, en la que el equilibrio se satisface mediante un flujo de cizalladura cerrado. Las secciones sólidas pueden modelarse mediante secciones equivalentes de pared delgada. Para las secciones no macizas, el espesor de pared equivalente no debe superar el espesor de pared real.

El flujo cortante en las paredes de una sección cerrada de pared delgada debido a la torsión puede calcularse como:

\[{{\tau }_{t}}\cdot {{t}_{ef}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\]

La fuerza cortante en una pared particular es entonces:

\{{V}_{i}={\tau }_{t}}\cdot {{t}_{ef}}\cdot {{l}_{i}}]

_li. . . . longitud del eje del muro considerado

Fuerza cortante en el alma: la longitud del eje del alma puede sustituirse por el valor del brazo de palanca "z".

\[{{V}_{ed,T}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cdot z\]

Fuerza en los estribos que resiste la torsión por un metro de la longitud del elemento (por unidad de longitud):

\[{{F}_{sw,T}}={frac{{V}_{ed,T}}{z\cdot \cot \theta }={frac{{T}_{ed}}{2{A}_{k}}\cdot tg\theta\]

Descomposiciones de fuerzas para estribo individual

Si se define el mismo material para todos los estribos, el esfuerzo resultante debido a la torsión en cada pata del estribo es constante. Entonces:

\[{{\sigma }_{sw,T}}=\frac{{{F}_{sw,T}}}{{{a}_{sw,T}}}\]

donde_asw,T es el área total de los estribos que resisten la torsión por unidad de longitud.

En el caso de que los estribos individuales tengan materiales diferentes, debe tenerse en cuenta la rigidez axial de las barras individuales.

\[{{F}_{sw,T}}={{F}_{s1,T}}+{{F}_{s2,T}}+{{F}_{s3,T}}+...+{{F}_{sn,T}}=\sum\limits_{i=1}^{{{n}_{T}}}{{{F}_{si,T}}}\]

\[{{\varepsilon }_{sw,T}}=\frac{{{F}_{sw,T}}}{\sum\limits_{i=1}^{{{n}_{T}}}{\left( {{a}_{si,T}}\cdot {{E}_{si,T}} \right)}}\]

_nT. . . . número de tramos de armadura (grupos de armaduras) que resisten la torsión

Fsi_,T. . fuerza en el i-ésimo grupo de armadura resultante de la torsión por unidad de longitud

_asi,T. . área transversal de la armadura de cortante que resiste la torsión por unidad de longitud

_Esi,T. . . Módulo de elasticidad de Young del i-ésimo grupo de armadura resistente a la torsión

εsw_,T. . deformación de la armadura debida a la torsión

La tensión resultante en cada estribo debido a la torsión aplicada se calcula como

\[{{\sigma }_{sw,i,T}}={{\varepsilon }_{sw,T}}\cdot {{E}_{si,T}}]

Interacción V+T

El cálculo de las tensiones en los estribos debidas al cizallamiento y a la torsión es entonces una suma de las tensiones debidas a los componentes individuales de la carga.

\[{{sigma }_{sw,i}}={{sigma }_{sw,i,V}}+{{sigma }_{sw,i,T}}]

Fuerza resultante en la i-ésima armadura:

\{{F}_{sw,i}={a}_{sw,i}\cdot {{sigma }_{sw,i}}]

Interacción de cortante, torsión y flexión para la armadura longitudinal

Determinación de la fuerza en cada armadura longitudinal debida a la fuerza normal y al momento flector

La aplicación RCS se utiliza para calcular la respuesta de la sección transversal debida a la combinación de la fuerza normal y el momento flector para determinar la tensión y la deformación en cada una de las barras longitudinales y la armadura de pretensado.

Determinación del esfuerzo en la armadura longitudinal individual debido al esfuerzo cortante

El incremento de la fuerza de tracción en la armadura longitudinal _ΔFtd debido a la fuerza cortante depende de la geometría del modelo de puntal y tirante.

\[\Delta {{F}_{td}}={{V}_{ed}}left( \cot \theta -\cot \alpha \right)\}]

_ΔFtd. . . incremento de la fuerza de tracción en la armadura longitudinal debido a la fuerza cortante.

_Ved. . . . valor de cálculo del esfuerzo cortante que actúa en la sección considerada

θ . . . . el ángulo entre el puntal de compresión de hormigón y el eje del elemento

α . . . . ángulo entre la armadura de cortante y el eje del elemento

Para la armadura longitudinal situada en el cordón de tracción, la fuerza resultante _Ft en la armadura longitudinal debida a la combinación N+M+V debe tomarse no mayor que_MEd,max/z(donde_MEd,max es el momento máximo a lo largo de la viga)

\[{{F}_{t}=\frac{{M}_{Ed}}{z}+0,5{{V}_{ed}}left( \cot \theta -\cot \alpha \right)\le \frac{{{M}_Ed,\max }}{z}}].

La fuerza _ΔFtd es transmitida por todos los tendones de pretensado adheridos y las armaduras situadas en la parte de la sección transversal que resiste el cortante (el alma en el caso de un perfil en I). Por seguridad, la contribución de la armadura de pretensado puede considerarse 0. La hipótesis del cálculo es que el incremento de la deformación axial de la armadura longitudinal individual que resiste el cortante es constante (Δεs1_,V = Δεs2_,V = .... =Δεp1_,V = Δεp2_,V = ... = _ΔεV = const.). La derivación es válida para un diagrama de trabajo de armadura bilineal con una rama plástica horizontal. En el caso de un diagrama con una rama inclinada, el cálculo debe modificarse.

\[\Delta {{F}_{td}}=\Delta {{F}_{s}}+\Delta {{F}_{s}}]

\[\Delta {{F}_{td}=\Delta {{varepsilon }_{V}}\cdot \sum\limits_{i=1}^{{{n}{s,V}}{{A}_{sl,i,V}}\cdot {{E}{sl,i,V}}+Delta {{varepsilon }_{V}}\cdot {{suma_limits_i=1}^{{n}}{p,V}}{{A}{pl,i,V}}\cdot {{E}{pl,i,V}}]

_ΔεV. . . . incremento de deformación en la armadura longitudinal debido al esfuerzo cortante.

ns_,V. . . . número de armaduras longitudinales que resisten el esfuerzo cortante

_Asl,i,V. . . área de la i-ésima armadura longitudinal que resiste el esfuerzo cortante

_Esl,i,V. . . Módulo de elasticidad de Young de la i-ésima armadura longitudinal que resiste el esfuerzo cortante

np_,V. . . . número de tendones que resisten el esfuerzo cortante

Apl_,i,V. . . área del tendón i-ésimo que resiste el esfuerzo cortante

Epl_,i,V. . . Módulo de elasticidad de Young del tendón i-ésimo que resiste la fuerza cortante

Una vez determinado el valor de la fuerza _ΔFtd, puede calcularse la deformación media de la armadura _ΔεV.

\[\Delta {{\varepsilon }_{V}}=\frac{\Delta {{F}_{td}}}{\sum\limits_{i=1}^{{{n}_{s,V}}}{{{A}_{sl,i,V}}\cdot {{E}_{sl,i,V}}}+\sum\limits_{i=1}^{{{n}_{p,V}}}{{{A}_{pl,i,V}}\cdot {{E}_{pl,i,V}}}}\]

Incremento de tensión en las barras longitudinales individuales debido al esfuerzo cortante aplicado:

para la barra corrugada \[\Delta {{sigma }_{sl,i,V}}=\Delta {{varepsilon }_{V}}\cdot {{E}_{sl,i,V}}].

para tendón \[\Delta {{sigma }_pl,i,V}}=\Delta {{varepsilon }_{V}}\cdot {{E}_{pl,i,V}}]

Determinación de la fuerza en cada armadura longitudinal por torsión

Es muy importante determinar las armaduras longitudinales que resisten la torsión. Estas son las armaduras que se encuentran en una sección transversal de pared delgada eficaz alternativa resistente a la torsión.

\[\frac{\sum{{{A}_{sl}}{{f}_{yd}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta \]

Según la norma EN 1992-1-1, deben cumplirse varias condiciones para el refuerzo resistente a la torsión longitudinal:

- la armadura debe distribuirse uniformemente a lo largo de la longitud _zi, pero en secciones transversales pequeñas la armadura puede concentrarse en las esquinas del estribo

- la distancia axial máxima de la armadura longitudinal es de 350 mm

La contribución de la armadura de pretensado no se considera según la norma EN 1992-1-1.

El código EN 1992-2 establece que se puede considerar la contribución de la armadura de pretensado, pero el incremento máximo de tensión en la armadura de pretensado no superará _Δσp ≤ 500MPa. Entonces se puede modificar la fórmula:

\[\frac{\sum{{{A}_{sl}}{{f}_{yd}}+\sum{{{A}_{p}}\Delta {{\sigma }_{p}}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta\]

Sin embargo, dado que se puede considerar el incremento del refuerzo de pretensado, pero queda a elección del usuario. Actualmente, la armadura de pretensado no se tiene en cuenta en el cálculo.

La hipótesis del cálculo es que el incremento de la deformación axial de cada armadura longitudinal resistente a cortante es constante (Δεs1_,T = Δεs2_,T = .... =Δεp1_,T = Δεp2_,T = ... = _ΔεT = const.). La derivación es válida para un diagrama de trabajo de armadura bilineal con una rama plástica horizontal. En el caso de un diagrama con una rama creciente, el cálculo debe modificarse.

\[\frac{\sum\limits_{i=1}^{{{n}_{T}}}{{{A}_{sl,i,T}}\cdot \Delta {{\sigma }_{s,i,T}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta\]

\[\frac{\sum\limits_{i=1}^{{{n}_{T}}}{{{A}_{sl,i,T}}\cdot \Delta {{\varepsilon }_{T}}\cdot {{E}_{s,i,T}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta\]

|Delta {{varepsilon }_{T}}={frac{{T}_{ed}}{cdot {{u}{k}}{2{A}_{k}}{cdot \sum\limits_{i=1}^{{{n}{T}}{{A}{sl,i,T}}cdot {{E}{s,i,T}}}}}}\cot \theta]

\[\frac{\sum\limits_{i=1}^{{{n}_{T}}}{{{A}_{sl,i,T}}\cdot \Delta {{\sigma }_{s,i,T}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta\]

\[\frac{\sum\limits_{i=1}^{{{n}_{T}}}{{{A}_{sl,i,T}}\cdot \Delta {{\varepsilon }_{T}}\cdot {{E}_{s,i,T}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta\]

|Delta {{varepsilon }_{T}}={frac{{T}_{ed}}{cdot {{u}{k}}{2{A}_{k}}{cdot \sum\limits_{i=1}^{{{n}{T}}{{A}{sl,i,T}}cdot {{E}{s,i,T}}}}}}\cot \theta]

_Ted. . . el valor de cálculo del par aplicado en la sección considerada

θ . . . . inclinación de las diagonales de compresión con respecto al eje longitudinal de la viga (idéntica a la del esfuerzo cortante)

uk . . . . perímetro del área_Ak

_Af. . . superficie definida por el eje de la sección hueca de pared delgada de sustitución

ns_,T. . . .número de armaduras longitudinales de hormigón que resisten el par de torsión

_Asl,i,T. . superficie de la i-ésima armadura longitudinal de hormigón que resiste el momento de torsión

_ΔεT. . . el cambio en la transformación de la armadura longitudinal debido al momento de torsión

Δσs_,i,T. . cambio de la tensión en la i-ésima armadura longitudinal debido al momento de torsión

_Esl,i,T. . módulo de elasticidad de la i-ésima armadura longitudinal de hormigón que resiste el momento de torsión

Incremento de tensión en cada armadura longitudinal debido al par aplicado:

\[\Delta {{sigma }_{sl,i,T}}=\Delta {{varepsilon }_{T}}\cdot {{E}_{sl,i,T}}].

Control de la limitación del estrés

La comprobación se basa en supuestos generales, en los que se resuelven dos estados de la sección transversal: la sección no fisurada (no se ignora la resistencia a tracción del hormigón) y la sección totalmente fisurada (se ignora la resistencia a tracción del hormigón).La solución con la resistencia a tracción del hormigón ignorada se considera bajo los supuestos del artículo 7.1 (2) EN 1992-1-1.

Al calcular la tensión y las deformaciones, se considera una sección no fisurada si la tensión de tracción en flexión no supera fct_{, eff}.El valor de fct_{, eff} puede considerarse como _fctm o fctm_,fl. El valor _fctm se utiliza al calcular la anchura de la fisura y la rigidez a tracción.

Como parte de esta comprobación, tratamos cuatro casos básicos en términos de límite de tensión.

• 7.2 (2) Debe limitarse la tensión de compresión en las barras expuestas a ambientes de las clases de exposición XD, XF y XS:

\[\left| {{s}_{c}} \right|le {{k}_{1}}{{f}_{ck}}]

\[{{k}_{1}}=0,6\]

• 7.2 (3) La tensión en el hormigón bajo las cargas cuasipermanentes está limitada:

\[\left| {{s}_{c}} \right|le {{k}_{2}}{{f}_{ck}}]

\[{{k}_{2}}=0,45\]

• 7.2 (5) Se limitarán los esfuerzos de tracción en la armadura bajo la combinación característica de cargas:

\[\left| {{s}_{s}} \right|le {{k}_{3}}{{f}_{yk}}]

\[{{k}_{3}}=0,8\]

• 7.2 (5) Cuando la tensión es causada por una deformación impuesta, la tensión de tracción no debe exceder:

\[\left| {{s}_{s}} \right|le {{k}_{4}}{{f}_{yk}}]

\[{{k}_{4}}=1\]

Donde los valores _k1, _k2, _k3, _k4 para uso en un País pueden encontrarse en su Anexo Nacional. Los valores recomendados son 0,8; 1 y 0,75 respectivamente, límite elástico característico de la armadura, _fck resistencia cilíndrica característica _fck determinada a 28 días.

Grietas

La formación de grietas

Un rasgo característico de las estructuras de hormigón armado sometidas a esfuerzos de flexión o tracción es la aparición de grietas en los puntos en los que el esfuerzo de tracción en el hormigón supera la resistencia a la tracción del hormigón. Para la durabilidad de la estructura y también para su estética, es importante garantizar que las grietas resultantes sean lo más pequeñas posible. El cálculo de la anchura de las fisuras, así como la anchura máxima permitida para las diferentes clases de exposición, se indican en la norma EN 1992-1-1, capítulo 7.3.

En el primer paso del cálculo, se determina si la sección transversal está agrietada o no. La propia anchura de la fisura se calcula siempre a partir de la combinación de carga cuasipermanente o frecuente (en función del anexo nacional), pero la formación de la fisura debe comprobarse a partir de todas las combinaciones de SLS especificadas. Por tanto, pueden darse dos casos:

• La tensión de tracción máxima en las fibras de hormigón no superará la resistencia a la tracción del hormigón a partir de ninguna combinación de carga (cuasipermanente_ME,qp, frecuente_ME,fr, o característica_ME,k), y por lo tanto consideramos la sección transversal sin fisuras.

\[{{M}_{E,i}}\le {{M}_{cr}}={{f}_{ct,ef}}\frac{{I}_{I}}{h-{{a}_{I}}}\]

• Si se desarrollan fisuras para cualquiera de las combinaciones (cuasipermanentes, frecuentes o características), es decir, el momento flector desarrollado a partir de la combinación de carga considerada es mayor que el momento crítico_Mcr, la sección transversal está fisurada a partir de esa combinación de carga, y deben calcularse las características de la sección transversal fisurada y la anchura de la fisura.

\[{{M}_{E,i}}>{{M}_{cr}}={{f}_{ct,ef}}\frac{{I}_{I}}{h-{{a}_{I}}}\]

_ME,i. . el momento flector obtenido a partir de algún peine de carga SLS. Por tanto, puede ser_ME,qp,_ME,fr o_ME,k.

fct_,ef . . la resistencia a tracción del hormigón en el momento considerado. Si el hormigón tiene más de 28 días, se considera una resistencia igual a _fctm.

Cálculo de la anchura de la fisura

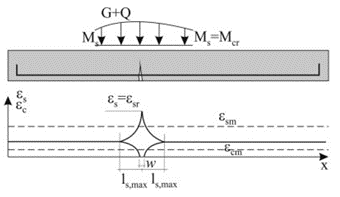
En un elemento sometido a flexión, la formación de grietas se divide en 2 fenómenos:

• Fase de formación de la grieta (etapa número 2 en la Fig. 1)
• Desarrollo estabilizado de la grieta (etapa número 3 en la Fig. 1)

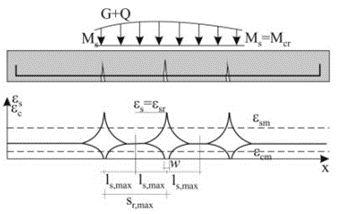
\[ \textsf{\textit{\footnotesize{Fig. 1 Etapas del comportamiento de la sección transversal de hormigón armado durante la carga}}]

Etapa de desarrollo de la grieta

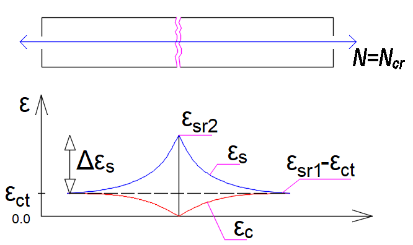
Se trata de la parte inicial del proceso, en la que las grietas individuales siguen apareciendo gradualmente hasta que toda la parte sometida a tracción del elemento se ve afectada por grietas que se distribuyen aproximadamente por igual a lo largo de la longitud del elemento. La primera grieta se forma cuando la fuerza en la banda sometida a tracción supera el valor de la fuerza crítica _Nr (fuerza de tracción crítica, véase más adelante), y se desarrollan más grietas hasta un nivel de carga que ejerce una fuerza en la banda sometida a tracción igual a 1,_3Ncr aproximadamente (fase número 2 en la Fig. 1).

\[ \textsf{\textit{\footnotesize{Fig. 2 Deformaciones del hormigón y la armadura en el momento de la primera fisura}}]

Las grietas en desarrollo se dividen en 2 tipos - grietas primarias y secundarias. Las grietas primarias se producen en las fibras de tracción cuando se alcanza la resistencia efectiva a tracción del hormigón (fct_,eff). Las grietas primarias representan el primer patrón de grietas (Fig. 2). A continuación, se forman grietas secundarias más cortas entre las grietas primarias (Fig. 3). A tensiones correspondientes a aproximadamente 1,2 a 1,5 _σsr (normalmente se considera un valor medio de 1,3 _σsr, donde _σsr es la tensión en la armadura en el momento de la formación de las fisuras primarias en la zona de tracción del hormigón), se completa también el desarrollo de las fisuras secundarias.

\[ \textsf{\textit{\footnotesize{Fig. 3 Fisuras primarias y secundarias}}]

La anchura de la grieta en la etapa de formación de grietas se puede calcular de la siguiente manera:

\[{{w}_{k}}=2{{l}_{s,\max }}left( {{\\varepsilon }_{sm}}-{\varepsilon }_{cm}} \right)\}]

\[ \textsf{\textit{footnotesize{Fig. 4 Características de la longitud de transmisión para la primera grieta}}]

Etapa de fisuración estabilizada

Después de superar aproximadamente 1,3 veces la fuerza crítica en la zona de tracción, no se forman nuevas grietas, el número de grietas en el elemento se estabiliza, y sólo la anchura de las grietas existentes aumenta con la carga adicional (etapa número 3 en la Fig. 1).

\[ \textsf{\textit{\footnotesize{Fig. 5 Deformaciones del hormigón y la armadura en la etapa de fisuración estabilizada}}]

La anchura de la grieta durante el desarrollo estable se puede calcular como:

\[{{w}_{k}={s}_{r,\max }}left( {{{varepsilon }_{sm}}-{{varepsilon }_{cm}} \right)\}]

\[ \textsf{\textit{footnotesize{Fig. 6 Agrietamiento estabilizado}}]

Fuerza de tracción crítica

El cálculo se basa en el Modelo de Cuerda de Tensión (TCM). La consideración básica es calcular la capacidad última de una banda de hormigón armado formada por una barra de refuerzo de área_As,eff rodeada por un área efectiva de hormigón de tracción_Ac,eff, que es capaz de resistir el esfuerzo de tracción hasta que se supera la resistencia a tracción fct_,eff (normalmente consideramos _fctm). Suponiendo una unión perfecta entre la armadura y el hormigón, podemos considerar que hasta que se produce la primera fisura, la remodelación de la armadura y del hormigón circundante es idéntica. Entonces se puede determinar la fuerza máxima en la banda de tracción justo antes de la primera fisura _Nr:

\[{{N}_{r}={A}_{c,eff}}\cdot {{f}_{ctm}}+{{A}_{s,eff}}\cdot {{sigma }_{s}}].

Introduciendo la sustitución

\[{{\alpha }_{e}}={}^{{{E}_{s}}}/{}_{{{E}_{cm}}};{{\rho }_{p,eff}}={}^{{{A}_{s,eff}}}/{}_{{{A}_{c,eff}}}\]

obtenemos:

\{{N}_{r}={A}_{c,eff}}\cdot {{f}_{ctm}}\cdot \left( 1+{{\alpha }_{e}}\cdot {{rho }_p,eff}} \right)\]

Justo después de la formación de la primera grieta, toda la fuerza _Nr es transferida por la armadura y por lo tanto la tensión en la armadura que pasa a través de la grieta recién formada se puede calcular como:

\{{{sigma }_{sr}}= {{frac{{f}_{ctm}}{{\rho }_{p,eff}} {{left( 1+{\alpha }_{e}} {{cdot {{\rho }_{p,Flecha derecha {{varepsilon}} = frac {{f}_{ctm}} {{E}{s} {\cdot {\rho }{p,eff}} {\left( 1+{alpha }_e} {\cdot {\rho }{p,eff}} {\right)\cdot]

Cálculo de la anchura de la grieta según CE 1992-1-1

La siguiente ecuación se utiliza para calcular la anchura de las fisuras en elementos de hormigón armado:

\[{{w}_{k}}={{s}_{r,\max }}left( {{\varepsilon }_{sm}}-{{\varepsilon }_{cm}} \right)\}]

_sr,max. . . separación máxima entre grietas

_εsm . . . la deformación media de la armadura a partir de la combinación de cargas, incluidos los efectos de la rigidización por tracción.

_εcm . . . deformación media del hormigón entre las fisuras

Cálculo de la diferencia de deformación

La diferencia de deformación de la armadura y del hormigón entre fisuras puede obtenerse a partir de la ecuación:

\[{{{varepsilon }_{sm}}-{{{varepsilon }_{cm}}=\frac{{{\sigma }_{s}}-{{k}_{t}}\cdot \frac{{{f}_{ct,eff}}}{{{{rho }_{p,eff}}}\cdot \left( 1+{{\alpha }_{e}}\cdot {{\rho }_{p,eff}} \right)\,}{{{E}_{s}}}\ge 0,6\frac{{{\sigma }_{s}}}{{{E}_{s}}}\]

σs_. . . . la tensión en la armadura en la fisura a partir de la combinación de cargas considerada

_{kt .} . . coeficiente empírico que tiene en cuenta la deformación media, en función de la duración de la carga. Puede tomar valores de 0,6 para el análisis a corto plazo. Para el análisis a largo plazo, se tiene en cuenta la reducción de la rigidez del material compuesto hasta aproximadamente el 70%, por lo que su valor es 0,4, que incluye la tasa de degradación de la cohesión entre la armadura y el hormigón debida al tiempo.

_αe. . . la relación efectiva de los módulos elásticos

\[{{\alpha }_{e}}={}^{{{E}_{s}}}/{}_{{{E}_{cm}}}\]

_ςp,eff. . . . . nivel efectivo de refuerzo

\izquierda( {{A}_{s,eff}}+{{xi }^2}_{1}A_{p}^{acute}} {derecha)}/{{A}_{c,eff}}]

_Ac, eff . . . . área efectiva del hormigón en tensión alrededor de la armadura (determinación de_Ac, eff más adelante)

_As,eff. . . . el área de la armadura adherida situada en el área de_Ac,eff

_Ap' . . . es el área de los tendones pretensados o postensados dentro de_Ac,eff

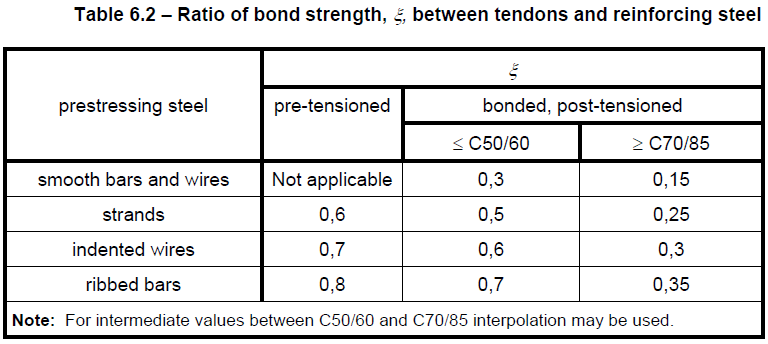
_ξ1. . . . es la relación ajustada de la resistencia de adherencia, teniendo en cuenta los diferentes diámetros del acero de pretensado y de armadura:

\[{{\xi }_{1}}=\sqrt{\xi \,\cdot \,\frac{{{\phi }_{s}}}{{{\phi }_{p}}}}\]

ξ . . . la relación entre la resistencia de adherencia del acero de pretensado y del acero de armadura (tabla 6.2)

_ϕs. . diámetro mayor de la barra de acero de refuerzo

_ϕp. . diámetro o diámetro equivalente del acero de pretensado

Para los haces,_Ap es el área de la armadura en el tendón

\[{{\phi }_{p}}=1,6\sqrt{{{A}_{p}}}\]

Para torones simples de siete alambres, donde _φwire es el diámetro del alambre

\[{{\phi }_{p}}=1,75\,\,{{\phi }_{hilo}}]

Para cordones simples de tres hilos en los que _φwire es el diámetro del hilo

\[{{\phi }_{p}}=1,20,\,{{\phi }__{hilos}}]

Si sólo se utiliza armadura de pretensado para evitar la fisuración, hay que tener en cuenta lo siguiente.

\[{{\xi }_{1}}=\sqrt{\xi \,}\]

En elementos pretensados, no se requiere un área mínima de armadura adherida siempre que, bajo la combinación característica de carga y el valor característico de la fuerza de pretensado, el esfuerzo de tracción en cualquier fibra no sea mayor que la resistencia a tracción del hormigón, fct_,eff. (véase EN 1992-1-1 cap. 7.3.2 para más detalles)

El área efectiva del hormigón en tensión

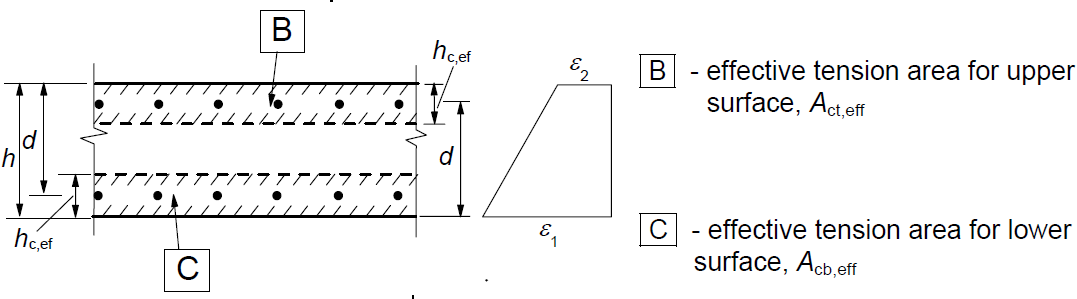
Un paso importante pero a la vez el más complicado del cálculo es determinar el área efectiva del hormigón en tracción que rodea la armadura. Tanto el Eurocódigo como el Código Modelo consideran modos de carga simples, en los que el elemento de hormigón armado se carga por flexión o tracción uniaxial. El valor de la altura efectiva se determina como:

\[{{h}_{c,eff}}=\min \left\{ 2,5\left( h-d \right);\frac{\left( h-x \right)}{3};{}^{h}/{}_{2}} {\i1}{\i}{\i} {\i}{\i} {\i}{\i}

\[ \textsf{\textit{footnotesize{Fig. 6 Determinación de Ac,eff para barras flexionadas (izquierda) y barras en tensión (derecha)}}]

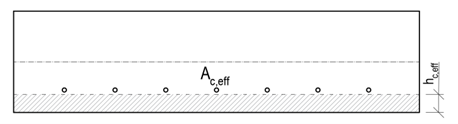
Normalmente, el valor hc_,eff = 2,5(h-d) es crítico. Para elementos tensados, el límite superior es h/2, mientras que para elementos flexionados es (h-x)/3. Sin embargo, el área_Ac,eff también está limitada por la anchura determinada a partir de la ecuación 5(c+ϕ/2). Si la separación de las armaduras es superior a 5(c+ϕ/2), entonces se considera el área efectiva del hormigón tensado de anchura 5(c+ϕ/2) para las barras individuales.

\[ \textsf{\textit{\footnotesize{Fig. 9 Determinación de Ac,eff en función de la separación entre armaduras}}]

Distancia máxima de fisura

Al calcular la distancia máxima de fisuración_sr,max, pueden darse dos casos:

• La distancia axial de las armaduras adheridas no supera una distancia de 5(c+ϕ/2) - Fig. 9a
• La distancia axial de las armaduras adheridas es superior a 5(c+ϕ/2) - Fig. 9b

El cálculo de la distancia máxima de fisuración_sr,max para el caso de que las distancias axiales de las armaduras no superen el valor 5(c+ϕ/2 ) se define como sigue:

\[{{s}_{r,\max }}={{k}_{3}c+{{k}_{1}}{{k}_2}}{{k}_{4}}frac{{\phi }{{\rho }_{p,eff}}].

c _. . . . valor de recubrimiento concreto en mm. Dado que el valor del recubrimiento puede ser diferente para la armadura de borde tanto horizontal como vertical, se recomienda considerar el valor máximo de recubrimiento encontrado para la armadura considerada.

_ϕ . . . . diámetro de la armadura adherida. En el caso de diámetros de armadura diferentes, el diámetro equivalente se calculará de acuerdo con la ecuación 7.12 de la norma EN 1992-1-1.

\[{{\phi }_{eq}}={\frac{{{n}_{1}\phi _{1}^{2}+{{n}_{2}\phi _{2}^{2}}{{{n}_{{phi }_{1}+{{n}_{2}}{{\phi }_{2}}].

_k1. . . . es un coeficiente que tiene en cuenta las propiedades de adherencia de la armadura adherida

• _k1 = 0,8 para barras de alta adherencia
• _k1 = 1,6 para barras con una superficie efectivamente lisa (por ejemplo, tendones de pretensado)

_k2. . . . es un coeficiente que tiene en cuenta la distribución de la deformación

• _k2 = 1,0 para flexión
• _k2 = 0,5 para tracción pura

Para los casos de tensión excéntrica o para zonas locales, deben utilizarse valores intermedios de _k2 que pueden calcularse a partir de la relación:

\[{{k}_{2}}=\frac{{\\varepsilon }_{1}}+{{\varepsilon }_2}}{2{\varepsilon }_{1}}].

k3_. . . coeficiente que expresa la longitud de la zona próxima a una fisura en la que se rompe la unión entre el hormigón y la armadura. El valor recomendado del CE básico _k3 = 3,4 puede ser modificado por el Anexo Nacional.

El coeficiente k4_. . . expresa la relación entre la adherencia y la resistencia a tracción del hormigón. El valor recomendado del CE básico k4 = 0,425 puede ser modificado por el Anexo Nacional.

El cálculo de la distancia máxima de fisuración_sr,max para el caso de que las distancias axiales de las armaduras superen el valor 5(c+ϕ/2) se define como sigue:

\[{{s}_{r,\max }}=1,3\left( h-x \right)\]

Valores máximos de distancia de fisura según la ecuación

\[{{s}_{r,\max }}=1,3\left( h-x \right)\]

deben ser siempre superiores a los valores determinados por la ecuación

\{{s}_{r,\max }}={k}_{3}c+{{k}_{1}{k}_2}}{k}_{4}{{phi }/{{rho }_p,eff}};\}].

de lo contrario, se recomienda considerar la distancia mayor obtenida a partir de las ecuaciones anteriores. La ecuación de la deformación en el hormigón/refuerzo no se modifica para el caso de la distancia axial grande del refuerzo. En zonas con anchuras de fisura controladas, la distancia axial de las armaduras individuales no debe ser superior a 5(c+ϕ/2).

Cálculo de la anchura de fisura implementado en RCS

Determinación del área efectiva_Ac,eff

Dado que no es tan sencillo determinar qué armadura puede considerarse como armadura longitudinal resistente a la fisuración,_Ac, eff se determina mediante el siguiente proceso iterativo.

• De todas las armaduras que actúan a tracción, se determina el centro de la fuerza de tracción Cg_,s,1. La profundidad efectiva de la armadura d es la distancia entre Cg_,s, y la fibra de hormigón más comprimida calculada en la dirección del momento flector resultante. Al mismo tiempo, se determinan la posición del eje neutro y la altura de la zona comprimida x para la sección fisurada. Esto permite determinar la altura efectiva hc_,eff:

\[{{h}_{c,eff}}=\min \left\{ 2,5\left( h-d \right);\frac{\left( h-x \right)}{3};{}^{h}/{}_{2}} {\a6}[\a6}[\a6}[\a6}[\a6]

• Excluyendo todas las armaduras que se encuentran fuera de_Ac,eff,1, se determina el nuevo centro de la armadura Cg_,s,2, junto con la nueva profundidad efectiva de la armadura d, la altura efectiva hc_, eff se determina de la misma manera que en el paso anterior, sólo que con los valores de entrada cambiados.

De nuevo, se comprueba que toda la armadura tensada considerada se encuentra en la_Ac,eff,2. Si esta condición se cumple, la iteración puede ser terminada y los valores de hc_,eff,2,_Ac,eff,2 y_As,eff,2 se muestran como los valores resultantes en IDEA StatiCa RCS.

Posibles casos de cálculo del ancho de fisura

En general, pueden darse tres casos en el cálculo del ancho de fisura:

• La armadura de tracción se encuentra en la región_Ac,eff, siendo la distancia axial de las armaduras individuales inferior a 5(c+ϕ/2). Entonces se utilizan las siguientes definiciones para el cálculo:

\[{{s}_{r,\max }}={{k}{3}c+{{k}_{1}}{{k}_2}}{{k}_{4}}frac{{\phi }{{\rho }_{p,eff}}].

\{ {{varepsilon }_{sm}}-{{\\varepsilon }_{cm}}={frac{{\sigma }_{s}}-{{k}_{t}},{\cdot,{frac{{{f}_{ct,eff}}}-{{\rho }_{p,eff}},\0,6frac {{sigma}} {{E}{s}}}]

• El refuerzo de tracción se encuentra en el_Ac,eff, con la distancia axial de los refuerzos individuales superior a la distancia 5(c+ϕ/2). A continuación, se utilizan las siguientes definiciones para el cálculo:

\[{{s}_{r,\max }}=1,3\left( h-x \right)\]

\[{{{varepsilon }_{sm}}-{{{varepsilon }_{cm}}={frac{{{sigma }_{s}}-{k}_{t}},\cdot \,\frac{{{f}_{ct,eff}}}{{{\rho }_{p,eff}},\0,6frac {{sigma}} {{E}{s}}}]

• La armadura de tracción no se encuentra en el_Ac,eff (esto puede deberse, por ejemplo, a una cubierta gruesa).

En este caso no sería posible calcular la anchura de las grietas. Por lo tanto, el cálculo de la altura efectiva hc_,eff se modifica como sigue:

\[{{h}_{c,eff}}=\min \left\{ 2,5\left( h-d \right);h/2 \right\}].

Al mismo tiempo, aparece la siguiente disconformidad:

El área efectiva de hormigón en tensión que rodea a la armadura o tendones de pretensado de profundidad hc_,eff, donde hc_, eff es el menor de 2,5(h - d) o h/2. Considerando el valor como(h - x)/3, la armadura está fuera del área efectiva de hormigón en tensión, y por lo tanto no sería posible calcular el ancho de fisura de acuerdo con la cláusula 7.3.4.

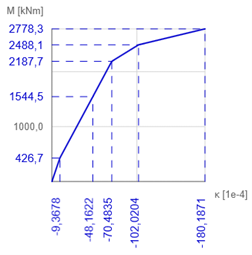
Diagrama N-M-κ

El diagrama N-M-κ muestra la curvatura de un elemento (rigidez a la flexión) en función de un momento flector y una fuerza normal aplicados. Existen tres tipos de diagramas N-M-κ:
- a corto plazo,
- a largo plazo
- ULS.
Estos diagramas difieren en los tipos de diagramas tensión-deformación utilizados para el cálculo (explicados a continuación).

El cálculo de la rigidez para los estados característicos seleccionados de la sección transversal se utiliza para determinar el diagrama N-M-κ. En general, puede ser cualquier estado de la sección transversal a partir del cual se calcula la respuesta y del que se derivan la rigidez a flexión y la curvatura. En IDEA RCS, consideramos cuatro puntos característicos (_Mr,_Mc,_Ms y_Mu)

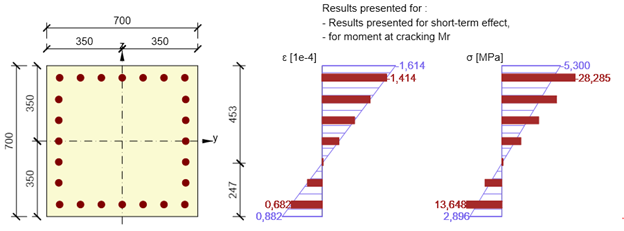
_Mr - el momento de fisuración

La sección transversal se somete a una fuerza normal definida por el usuario y el plano de deformación comienza a girar (en la dirección del momento de flexión especificado) hasta que se alcanza la resistencia última a la tracción del hormigón en una fibra de hormigón (para el grado de hormigón C30/37 es _fctm = 2,896 MPa). Para el cálculo se utiliza un diagrama de tensión-deformación bilineal con una rama plástica horizontal tanto para la armadura como para el hormigón.

_Mc - el momento flector cuando se alcanza la resistencia a la compresión del hormigón

A partir del paso anterior, se identifica la fibra de hormigón más utilizada en compresión. Para esta fibra, se establece la deformación a la resistencia última del hormigón (_fck/Ecm para corto plazo, _fck/Eceff para largo plazo y _fcd/Ecm para el diagrama ULS). A partir de la fuerza normal definida y la dirección del momento flector, se ejecuta el proceso de iteración para encontrar el plano de deformación con el fin de encontrar un equilibrio entre la respuesta de la sección transversal y la fuerza normal definida. Para el cálculo se utiliza un diagrama de tensión-deformación bilineal con una rama plástica horizontal tanto para la armadura como para el hormigón.

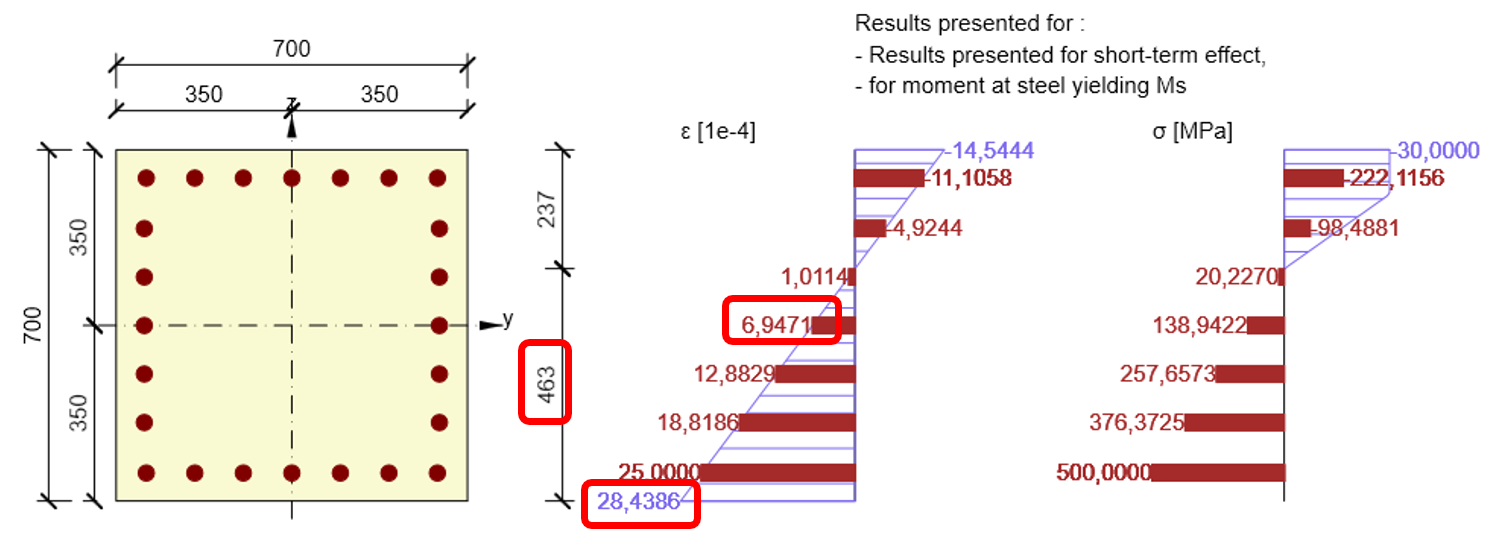
_Ms - el momento flector cuando se alcanza el límite elástico en la barra de refuerzo más utilizada

Otro punto característico del diagrama N-M-κ es el estado tensional de la sección transversal cuando se alcanza el límite elástico en la barra de armadura más utilizada (la deformación de la armadura es igual a _fyk/Es para los diagramas a corto y largo plazo, _fyd/Es para el diagrama ULS). El proceso de iteración encuentra un equilibrio de fuerzas normales en la sección transversal girando el plano de deformación alrededor del punto especificado por la posición de la barra de refuerzo más utilizada. Para el cálculo se utiliza un diagrama tensión-deformación bilineal con una rama plástica horizontal tanto para la armadura como para el hormigón.

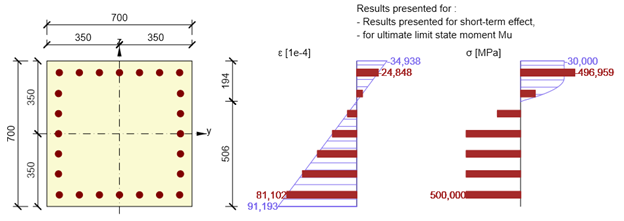
_Mu - el momento flector en el estado límite último

Es la capacidad de carga última de una sección transversal en flexión, cuando la sección transversal está sometida a una fuerza normal de diseño definida _Ned. Para el cálculo de la capacidad de la sección transversal, se supone que se alcanza la resistencia a la compresión en la fibra de hormigón más utilizada y la resistencia a la tracción en la barra de armadura más utilizada (deformación máxima para el hormigón _εcu = 0,1 y para la armadura εs_,max = 0,5). Para el cálculo se utiliza un diagrama tensión-deformación bilineal con una rama plástica horizontal para la armadura y un diagrama parábola-rectangular para el hormigón.

La rigidez y la curvatura resultantes debidas a la combinación definida por el usuario de fuerza normal y momento flector ( Md) se calculan a continuación mediante interpolación lineal de los puntos característicos individuales del diagrama N-M-κ.

Cálculo de rigideces y curvaturas

Las rigideces y curvaturas para cada estado de tensión transversal (_Mr,_Mc,_Ms o_Mu) se calculan directamente a partir de la rotación del plano de deformación.

\[E{{A}_{x}}=\frac{N}{{{\varepsilon }_{x}}}\]

_EAx. . rigidez axial del elemento

N . . . la fuerza normal especificada

_εx. . . deformación axial en el centro de gravedad de la sección transversal de hormigón

\[E{{I}_{y}}=\frac{M}{\kappa }\]

_EIy. . . rigidez a flexión del elemento

M . . . el momento flector calculado_Mr,_Mc,_Ms o_Mu

κ . . . . la curvatura del elemento, calculada como la tangente del ángulo entre el plano de deformación y el eje longitudinal del elemento

Ejemplo práctico

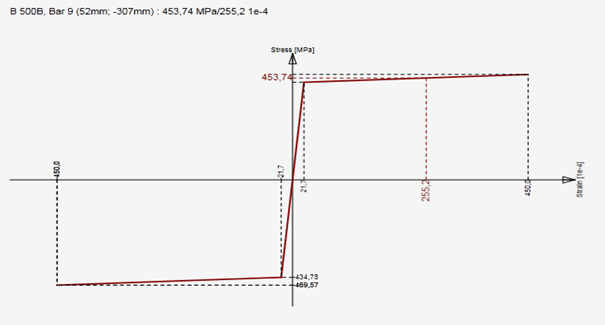
Una sección transversal de hormigón (grado de hormigón C30/37) se refuerza con ϕ32 armaduras (grado B500B). La combinación cuasipermanente definida es N = -730 kN y_My = 557 kNm.

El plano de deformación para el punto característico_Ms se determina mediante IDEA RCS de la siguiente manera:

\[E{{A}_{x}}=\frac{N}{{{\varepsilon }_{x}}}=\frac{730}{6,9471\cdot {{10}^{-4}}}=1050,798MN\]

\[\kappa =\frac{28,4386\cdot {{10}^{-4}}{0,463}=61,422\cdot {{10}^{-4}}{{m}^{-1}}]

\[E{{I}_{y}}=\frac{{{M}_{s}}}{\kappa }=\frac{2277,4}{61,422\cdot {{10}^{-4}}}=370,776MN{{m}^{2}}\]

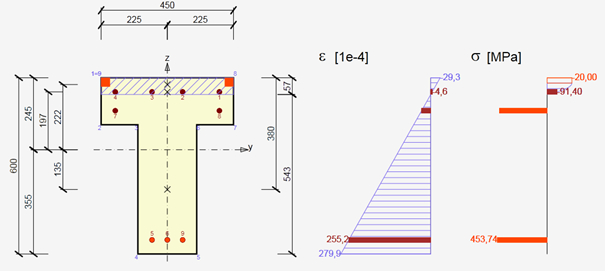
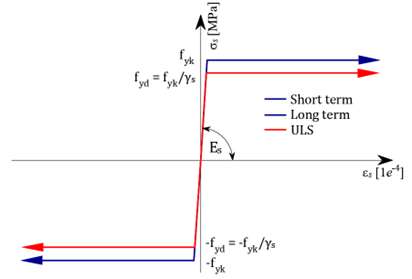
Diagramas tensión-deformación utilizados para el cálculo

Refuerzo -_Mr,_Mc,_Ms y_Mu

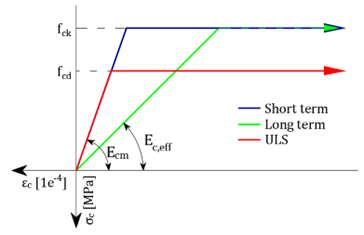
Hormigón -_Mr,_Mc,_Ms

Hormigón -_Mu

Literatura

[1] Bradáč Betonové konstrukce (estructuras de hormigón), 1.part: Dimensioning of members from reinforced and plainconcrete, EXPERT Ostrava, 1996

[2] ČSN EN 1992-1-1 (73 1201) Eurocódigo 2: Diseño de estructuras de hormigón - Parte 1-1: Reglas generales y reglas para edificios, inc. cambio NA ed. A (2007) y revisión 1 (2009)

[3] ČSN EN 1992-2 (73 6208) Eurokód 2: Navrhování betonových konstrukcí - Část 2: Betonové mosty - Navrhování a konstrukční zásady

[4] Navrátil, J. Předpjaté betonové konstrukce. 2. vydání, Akademické nakladatelství CERM, Vysoké učení technické v Brně, Fakulta stavební, 2008.

[5] Šmiřák, S. Pružnost a plasticita I, Vysoké učení technické v Brně, Akademické nakladatelství CERM, Brno, 1999.

[6] Vondráček, R. Numerical Methods in Nonlinear Concrete Design, Diplomová práce, ČVUT, Praha, 2000.

[7] Zich, M. a kolektiv Konstrukční Eurokódy - Příklady posouzení betonových prvků dle Eurokódů, libro en línea http://www.stavebniklub.cz/konstrukcni-eurokody-onbecd/, Verlag Dashöfer, 2010.