Schuifmuur met verspringende openingen

De belangrijkste functie van keerwanden is het weerstaan van zijdelingse belastingen die optreden tijdens aardbevingen, windstormen of andere dynamische gebeurtenissen. Door de krachten over te brengen naar de fundering van het gebouw, helpen ze de structurele schade te minimaliseren en de integriteit van de constructie te behouden. Schuifwanden worden strategisch geplaatst binnen de plattegrond van een gebouw om de effectieve verdeling van laterale belastingen te garanderen. Ze worden meestal geplaatst aan de rand van het gebouw of in de buurt van de kern van het gebouw. In hoogbouw worden schuifwanden vaak rond lift- en trapschachten geplaatst voor extra stijfheid en stabiliteit. Schuifwanden bieden verschillende voordelen, waaronder een grotere structurele stabiliteit, een betere weerstand tegen zijdelingse belastingen en een verbeterde algemene veiligheid tijdens seismische gebeurtenissen. Bovendien kunnen ze bijdragen aan het architectonisch ontwerp door mogelijkheden te bieden voor creatieve expressie terwijl ze hun structurele functie vervullen.

Modelbeschrijving

Er zijn vier verificatiemodellen opgesteld om de resultaten te evalueren. Twee van deze modellen houden rekening met de karakteristieke materiaaleigenschappen, terwijl de andere twee zijn gebaseerd op ontwerpwaarden volgens Eurocode 1992-1-1[3]. Deze verificatiemodellen zijn gebaseerd op de Compatible Stress Field Theory (CSFM)[1] en het Drucker-Prager Plasticity Model[2].

Let voor een beter begrip op de volgende modelidentificatie:

• Detail - Karakteristiek
• Detail - Ontwerp
• ABAQUS - Karakteristiek
• ABAQUS - Ontwerp

Geometrie en materialen

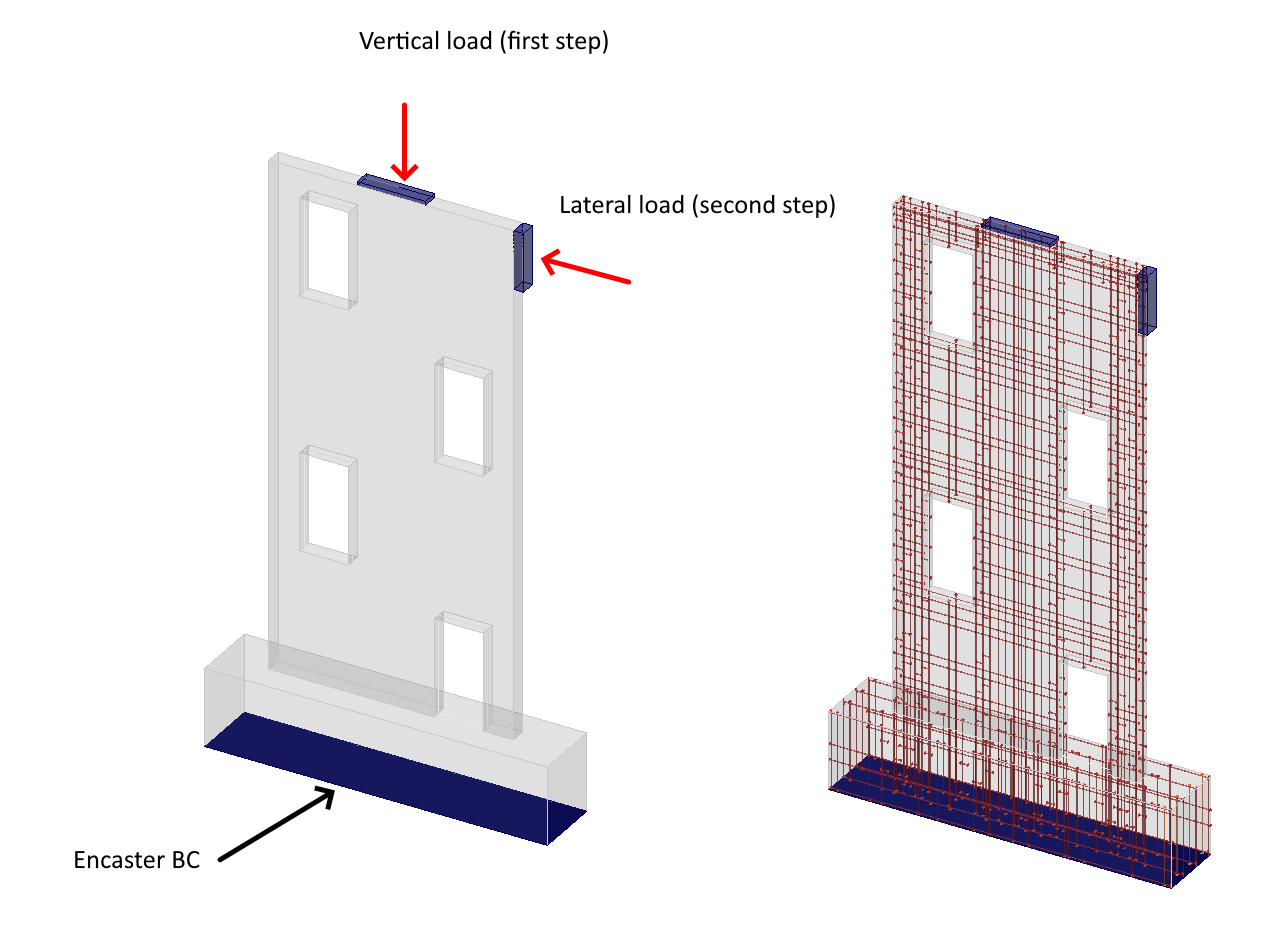
Het testmodel is met een factor vier verkleind ten opzichte van de werkelijke grootte. De fundering van de constructie meet 1750 mm x 400 mm x 350 mm, terwijl de wanden afmetingen hebben van 1250 mm x 2600 mm x 80 mm. De muren zijn verdeeld in vier niveaus met verspringende openingen van elk 250 mm x 500 mm. Het gebruikte beton is van kwaliteit C35/45 en is gewapend met B500B en een diameter van 6 mm. De belastingen worden overgebracht met extra platen van constructiestaal S235.

Fig. 1) Geometrie

Compatibele spanningsveldmethode

Veronderstellingen

CSFM beschouwt de maximale hoofdspanningen van beton in compressie (_σc2r) en wapeningsspanningen (_σsr) bij de scheuren terwijl de betontreksterkte (_σc1r = 0) wordt verwaarloosd, behalve voor het verstijvingseffect op de wapening. Door rekening te houden met trekverstijving kunnen de gemiddelde wapeningsspanningen (_εm) worden gesimuleerd. Meer informatie over de theorie kan worden gevonden in Theoretische achtergrond.

Fig. 2) Compatibele spanningsveldmethode - Veronderstellingen

Drucker-Prager Plasticiteitsmodel (DPPM)

Veronderstellingen

Concrete Damage Plasticity (hierna CDP) is gebaseerd op de Drucker-Prager plasticiteitsconditie. Dit model is geschikt voor materialen met interne wrijving, zoals grond of beton. De treksterkte is lager dan de druksterkte en het hydrostatische deel van de spanningst tensor speelt een rol in de evolutie van het plasticiteitsoppervlak. Onder algemene spanning heeft de plasticiteitstoestand het oppervlak van een roterende kegel. Het materiaalmodel voor druk- en trekspanningen houdt ook rekening met postkritisch gedrag, dat wordt gecontroleerd door de zogenaamde schadeparameters, die waarden aannemen van nul tot één (voor bijna-nul elastische stijfheid van beton in druk of trek in de postkritische toestand). Hoe groter het getal van de schadeparameter, hoe meer het element geschonden wordt en niet bijdraagt aan de stijfheidsbijdrage.

Het eenassig materiaalmodel in samendrukking en trek voor beton is gebaseerd op de theorie van Thorenfeldt[4]. Alle invoergegevens zijn ontwerpwaarden die de betrouwbaarheidsbenadering van EN 1992-1-1[3] volgen. Er wordt rekening gehouden met het materiaalmodel van wapening B500B met trekverstijving. Meer informatie over de theorie.

Fig. 3) Materiaalmodel in druk (links), Drucker-Prager plasticiteitsoppervlak (midden), materiaalmodel in spanning (rechts)

Numerieke modellen

Compatibele spanningsveldmethode - IDEA StatiCa Detail

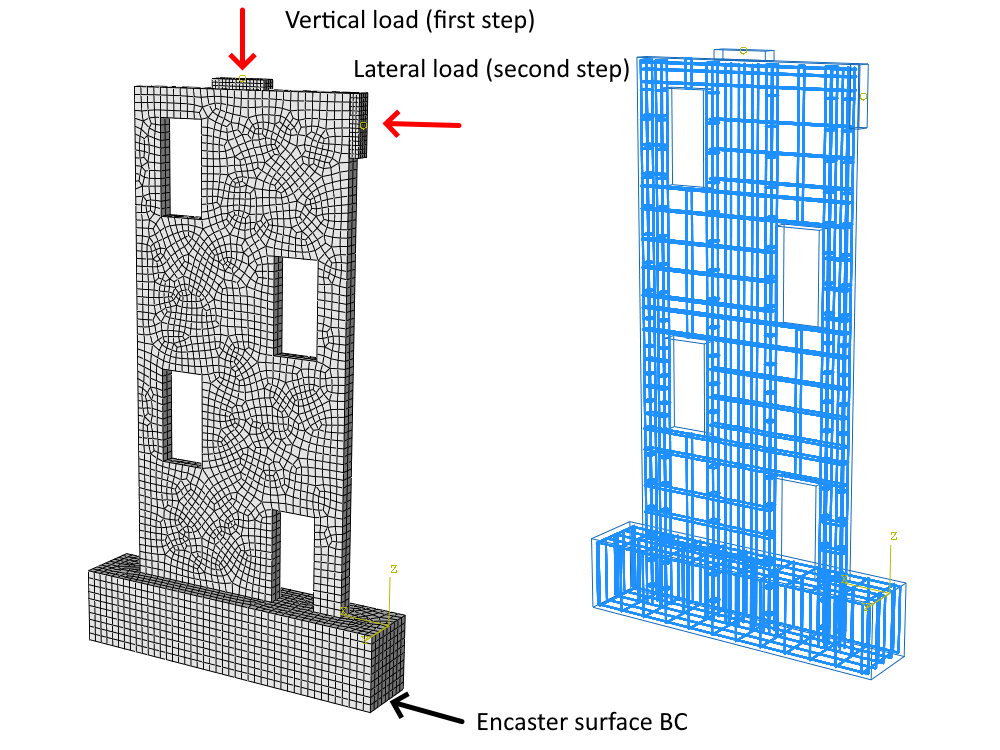
Het numerieke model bestaat uit 2D vlakke betonelementen en onderling verbonden 1D wapeningsstaven via MPC en verbindingselementen met de betondelen. Het model bevat twee dragende elementen in de vorm van stalen platen. De bovenste plaat van 350 x 80 x 20 mm draagt een verticale belasting van 50 kN als eerste stap van het belastingsproces. De tweede plaat, van 350 x 80 x 50 mm, wordt gebruikt als de tweede stap voor zijdelingse belasting in het wandvlak en zorgt voor een gelijkmatige verdeling van de geconcentreerde kracht tijdens het belasten van de wand. Het model is omhuld, waardoor de vrijheidsgraden Tx, Tz en Ry worden beperkt, en gaat uit van 2D vlakke spanningscondities.

Fig. 4) Numeriek model in IDEA StatiCa Detail (belastingsproces)

Drucker-Prager Plasticiteitsmodel

Het numerieke model bestaat uit 3D hexahedrale elementen gewapend met staven die star zijn beperkt binnen het gastbetongebied. Het beton en de voorgespannen wapening bestaan uit T3D2-elementen die alleen axiale effecten overbrengen. Het optreden van slip tussen beton en wapeningscomponenten wordt volledig beperkt door starre beperkingen. De slip wordt gesimuleerd door spanningsverzachting in beton, wat leidt tot elementverwijdering bij het bereiken van 70% schade in de postkritische toestand. Deze benadering houdt tot op zekere hoogte rekening met het cohesiemodel of het deuveleffect. De modeleigenschappen voor model en platen komen precies overeen met de aannames van CSFM.

Fig. 5) Numeriek model in ABAQUS (belastingsproces)

Analyse

Het belastingsproces omvat de incrementele toename van vervormingen in de laterale richtingen als onderdeel van het monotone belastingsproces. In deze analyse is geen rekening gehouden met cyclische belasting.

De numerieke benaderingen verschillen enigszins tussen de oplossingen vanuit het oogpunt van de analyse. CSFM gebruikt de theorie van de kleine vervorming en omvat de niet-lineaire analyse van het materiaal. Het Drucker-Prager- en ABAQUS-model maken daarentegen gebruik van geometrische en materiële niet-lineaire analyse, wat een nauwkeurigere oplossing biedt bij grote vervormingen.

Mesh-gevoeligheid

De gevoeligheidsanalyse geeft inzicht in de discrepanties die ontstaan door de discretisatie. De standaardconfiguratie voor CSFM heeft een maasvermenigvuldigingsfactor van één, wat overeenkomt met de regel om minimaal vier elementen op te nemen op de kleinste rand binnen het model. Vervolgens wordt het hele model overeenkomstig deze regel gemaasd. Dezelfde strategie is gebruikt voor het model in ABAQUS.

Compatibele spanningsveldmethode - IDEA StatiCa Detail

De gegevens tonen aan dat de gemiddelde fout tussen maasvermenigvuldigers van 0,5 en 2,0 7% is. Dit leidde tot een numerieke aanpak met een lage gevoeligheid.

Fig. 6 Netgevoeligheid IDEA StatiCa Detail

Drucker-Prager Plasticiteitsmodel

Het gebruik van 3D hexahedrale elementen resulteert in een bijna identieke maximale kracht bij gebruik van een mesh-vermenigvuldigingsfactor van 1,0 en 2,0. Het verschil in maximaal toelaatbare kracht bedraagt 1,3%. Het verschil in de maximaal toelaatbare kracht bedraagt 1,3%, wat een maasongevoelige oplossing suggereert. Het model gaat uit van een dilatatiehoek van 30 graden voor analysedoeleinden.

Fig. 7) Netgevoeligheid ABAQUS

Resultaten

De volgende informatie moet worden opgemerkt: De verstrekte waarden, zoals hoofdspanning in compressie, vervormingen, maximale spanning in compressie en spanning op de wapeningsstaaf en de locatie van schade, worden geïllustreerd in de volgende figuren. Alle waarden worden gepresenteerd voor een maasvermenigvuldigingsfactor van 1,0, die is gebruikt als verificatieparameter in CSFM[1] en vervolgens is toegepast op de Drucker-Prager-oplossing in ABAQUS[2]. De dilatatiehoek die wordt gebruikt op het Drucker-Prager plasticiteitsoppervlak is ingesteld op 30 graden. De resultaten worden gepresenteerd voor karakteristieke en ontwerp materiaaleigenschappen die zijn geëvalueerd op basis van de Eurocode 1992-1[3].

Hoofdspanningen in samendrukking

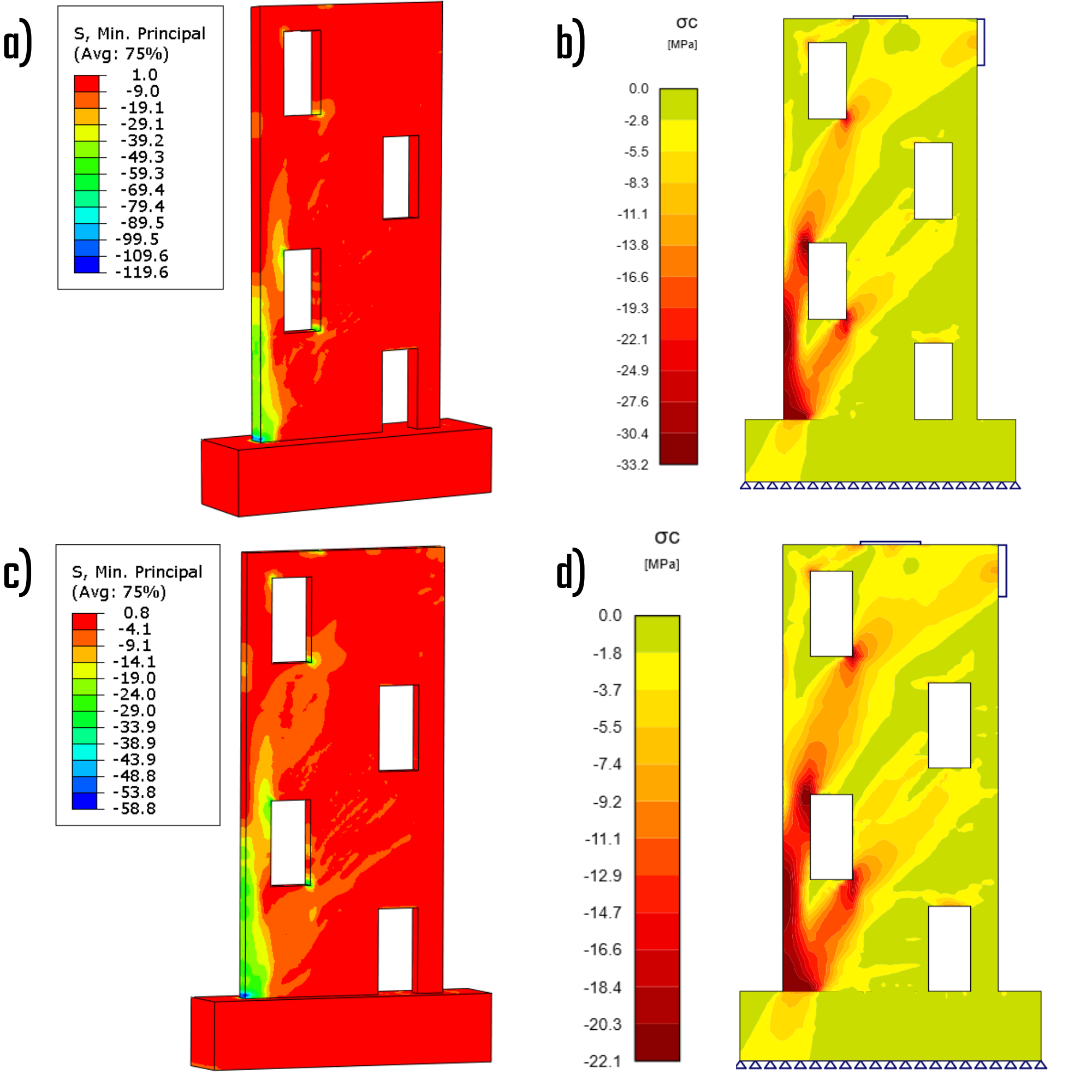
Het primaire onderscheid tussen de CSFM-oplossing en de Drucker-Prager-oplossing heeft betrekking op hun behandeling van spanning. De Drucker-Prager oplossing bevat opsluitdruk die de minimale hoofdspanning onder compressie aanzienlijk kan verhogen, waardoor het materiaal bestand is tegen hoge spanningsniveaus. Omgekeerd bepaalt de CSFM-oplossing de maximale karakteristieke of ontwerp uniaxiale sterkte van het materiaal, wat een gemakkelijke vergelijking met standaard materiaalbibliotheken mogelijk maakt. De spanningsverdelingen van de oplossingen vertonen opmerkelijke variaties in gebieden waar het opsluitingseffect uitgesproken is.

Fig. 8) a) Hoofdspanning in samendrukking - karakteristiek (ABAQUS); b) Hoofdspanning in samendrukking - karakteristiek (IDEA StatiCa); c) Hoofdspanning in samendrukking - ontwerp (ABAQUS); d) Hoofdspanning in samendrukking - ontwerp (IDEA StatiCa)

Spanningen in wapening

De spanning die de wapeningsstaven ondervinden biedt waardevolle informatie over de consistentie van de resultaten en de specifieke gebieden waar hoge spanningen geconcentreerd zijn.

Fig. 9) a) Spanning in staven - karakteristiek (ABAQUS); b) Spanning in staven - karakteristiek (IDEA StatiCa); c) Spanning in staven - ontwerp (ABAQUS); d) Spanning in staven - ontwerp (IDEA StatiCa)

Vervormingen

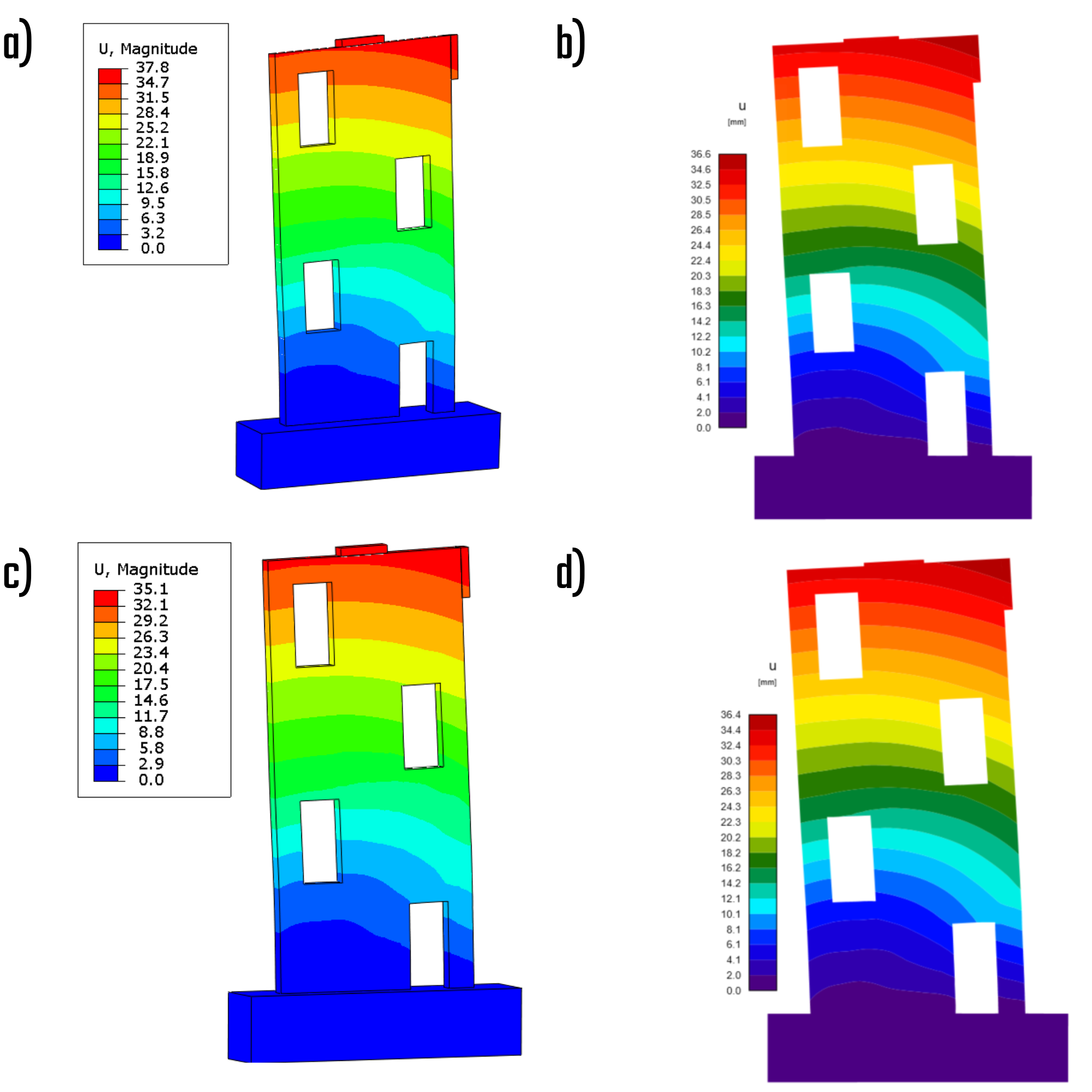
De vervormingen dienen als bewijs dat de geometrische niet-lineariteit verwaarloosbare implicaties heeft, gezien de consistentie die verzekerd wordt door de CSFM-oplossing en de niet-lineaire materiaalanalyse. Dit suggereert dat, voor het specifieke wandmonster in kwestie, het tweede orde effect geen invloed heeft op het structurele gedrag.

Fig. 10) a) Totale vervormingen - karakteristiek (ABAQUS); b) Totale vervormingen - karakteristiek (IDEA StatiCa); c) Totale vervormingen - ontwerp (ABAQUS); d) Totale vervormingen - ontwerp (IDEA StatiCa)

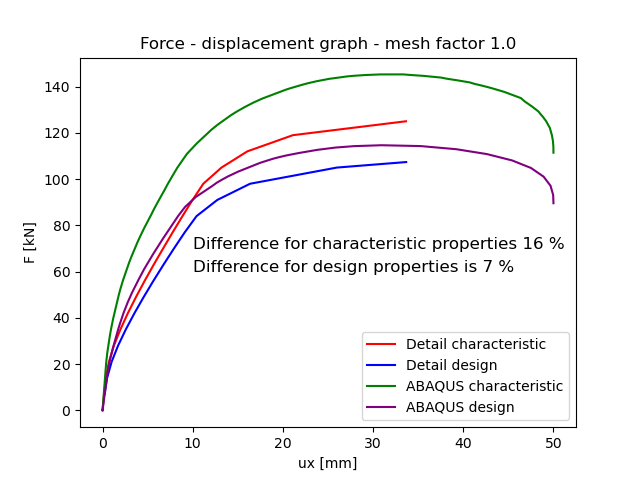
Grafiek kracht-vervormingen

De grafische weergave verduidelijkt op effectieve wijze de complexe reactie van de muur op laterale belasting. De CSFM-oplossing geeft een vermindering van de draagkracht aan van ongeveer 16% voor karakteristieke materiaaleigenschappen en 7% voor ontwerp materiaaleigenschappen. Deze verschillen komen voort uit de opname van het trekgedrag van beton in het Drucker-Prager Plasticity Model. De afwijkingen van 16% en 7% die zijn waargenomen in de CSFM-oplossing vallen binnen een acceptabele veiligheidsmarge.

Fig. 11) Grafiek krachtvervorming

Conclusie

Het onderzoek benadrukt de kritieke rol van dwarsmuren bij het weerstaan van zijdelingse belastingen door dynamische gebeurtenissen zoals aardbevingen en windstormen, waardoor de structurele stabiliteit en veiligheid worden gewaarborgd. Schuifmuren, strategisch geplaatst in gebouwontwerpen, helpen bij het verdelen van dwarskrachten, vooral in hoogbouw, doordat ze zich vaak rond lift- en trapschachten bevinden.

De analyse maakte gebruik van vier verificatiemodellen gebaseerd op zowel karakteristieke als ontwerpwaarden volgens Eurocode 1992-1-1, waarbij gebruik werd gemaakt van de Compatible Stress Field Method (CSFM)[1] en het Drucker-Prager Plasticity Model (DPPM)[2]. De studie omvatte verkleinde modellen en gedetailleerde geometrische en materiaalspecificaties, met aannames die op maat waren gemaakt voor elke analysemethode.

CSFM richtte zich op maximale hoofdspanningen van beton en wapeningsspanningen, waarbij de treksterkte van beton werd verwaarloosd, met uitzondering van verstijvingseffecten. DPPM daarentegen hield rekening met interne wrijving, trek- en druksterkte en postkritisch gedrag door schadeparameters. Voor beide methoden werden numerieke modellen gemaakt met verschillende benaderingen van belasting en beperkingen.

Mesh gevoeligheidsanalyse gaf een lage gevoeligheid aan voor beide methoden, met kleine verschillen in spanningsverdelingen en vervormingen. De resultaten benadrukten de verschillen in spanningsbehandeling, vooral met opsluitdruk in DPPM, en toonden aan dat geometrische niet-lineariteit verwaarloosbare effecten had op vervormingen.

Over het geheel genomen toonden de kracht-vervormingsgrafieken de reactie van de muur op laterale belastingen, waarbij CSFM-oplossingen acceptabele afwijkingen vertoonden ten opzichte van DPPM, wat de robuustheid van beide benaderingen bevestigde bij het waarborgen van de structurele integriteit onder laterale krachten.

Referenties

[1] IDEA StatiCa (n.d.). Theoretische achtergrond voor IDEA StatiCa Detail. Opgehaald op 30 mei 2024 van https://www.ideastatica.com/support-center/theoretical-background-for-idea-statica-detail

[2] Abaqus analysis gebruikershandleiding. Abaqus analysis gebruikershandleiding [online] www: https://classes.engineering.wustl.edu/2009/spring/mase5513/abaqus/docs/v6.6/books/usb/default.htm?startat=pt05ch18s05abm36.html

[3] EN 1992-1-1 Eurocode 2: Ontwerp van betonconstructies - Deel I: Algemene regels en regels voor gebouwen. Europees Comité voor Normalisatie, 2002.

[4] Massone, L. M.; et al. Shear-Flexure Interaction for Structural Walls, 2006. ResearchGate. https://www. researchgate.net/publication/284079633_Shear-flexure_interaction_for_structural_walls (bekeken op 01 jan 2006).