Hipótesis de cálculo
El comportamiento de una sección de hormigón armado sometida a torsión puede dividirse en dos categorías: antes y después del momento en que cabe esperar que se produzcan las primeras fisuras. Antes de la fisuración, la sección se comporta como un material elástico. El esfuerzo de torsión puede expresarse mediante la fórmula
\[\tau =~\frac{{{T}_{Ed}}}{{{W}_{t}}}\]
donde Wt je módulo seccional en torsión.
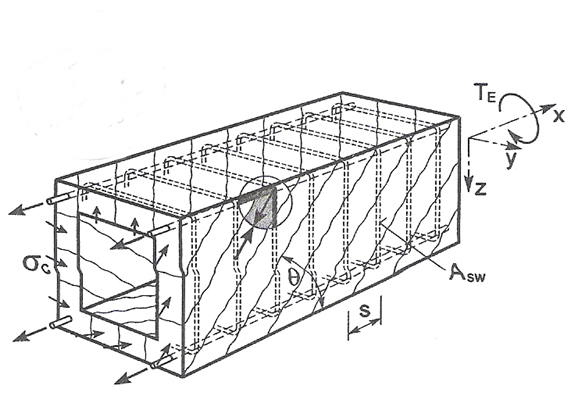
Las fisuras en el miembro no reforzado debidas al esfuerzo principal de torsión son también estados límite últimos. El comportamiento de una sección de hormigón armado sometida a torsión puede describirse a partir de una sección cerrada de pared delgada, véase la Fig. siguiente.
\Sección transversal de pared delgada equivalente.
Procedimiento de cálculo
El proceso de comprobación del hormigón armado a torsión es muy similar al de comprobación a cortante. En primer lugar, se comprueba la resistencia del hormigón.Si la comprobación del hormigón se cumple, la armadura puede diseñarse utilizando las reglas de detalle. En caso contrario, necesitamos comprobar la armadura y la resistencia diagonal a compresión mediante cálculo.
\Diagrama de proceso para la comprobación de torsión.
Resistencia
El flujo cortante en una pared de sección delgada sometida a torsión puede expresarse como:
\[ {{\tau }_{t}}{{t}_{ef}}=~\frac{{{T}_{Ed}}}{2{{A}_{k}}]
La fuerza cortante en una pared de una sección transversal de pared delgada puede expresarse como:
\[ V={\tau }_{t}}{{t}_{ef}}z]
Donde
τ Flujo cortante en la pared,
tef es el espesor efectivo de la pared,
z es la longitud lateral de la pared,
TEd es el momento de torsión,
Ak es el área encerrada por las líneas centrales de las paredes de conexión, incluyendo las áreas huecas interiores.
El momento de torsión, que puede determinarse ajustando fctd a la expresión anterior. Así obtenemos la expresión para la resistencia en torsión sin refuerzo de torsión.
\[ {{T}_{Rd,c}}=2{{A}_{k}}{{t}_{ef}}{{f}_{ctd}}\]
donde fctd resistencia a tracción axial de diseño del hormigón
\[ \textsf{\textit{\footnotesize{\qquad Principios de la analogía de la cercha para el miembro bajo momento de torsión.}}]
La resistencia del elemento con refuerzo de torsión se compone a partir de la resistencia a compresión de las diagonales de hormigón, que se basa de nuevo en el método de analogía de celosía. El esfuerzo de compresión en la diagonal se puede expresar con la ayuda del esfuerzo cortante en la pared de una sección transversal de pared delgada en la superficie de la pared que se está considerando, es decir
\[{{sigma }_{c}}={frac{\frac{{T}_{Ed}}z}{2{{A}_{k}}sin \theta }}{z~{t}_{ef}}cos \theta }={frac{{T}_{Ed}}{2{{A}_{k}}{t}_{ef}}sin \theta \cos \theta }].
Sustituyendo σc=σcwfcd yTEd=TRd,max y expresandoTRd,max obtenemos una ecuación para la resistencia diagonal a compresión
\[{{T}_{Rd,max}}=2~\nu ~{{\alpha }_{cw}}~{{f}_{cd}}~{A}_{k}~{t}_{ef~\sin \theta ~cos \theta }]
donde
ν = 0,6 pro fck ≤ 60MPa o para fck > 60MPa
Coeficiente αcw que tiene en cuenta el estado del esfuerzo de compresión en el cordón de compresión
fcd valor de cálculo de la resistencia a compresión del hormigón
la resistencia de la armadura de cortante sometida a torsión se basa de nuevo en el esfuerzo en la diagonal de compresión. La fuerza de estribo es igual a la tensión en la diagonal de compresión en el área que corresponde a la línea de estribo particular, es decir
\[{{A}_{sw}}{{f}_{ywd}}={frac{{T}_{Ed}}{2{{A}_{k}}{t}_{ef}}sin \theta \cos \theta }~{t}_{ef}}~{sin }^{2} {theta ={frac{{T}_{Ed}}{s}2{{A}_{k}}cot \theta }~].
SustituyendoTEd=TRd,s y expresandoTRd, s obtenemos la ecuación:
\[{{T}_{Rd,s}}=2{{A}_{k}}\frac{{{A}_{sw}}{{f}_{ywd}}}{s}~\cot \theta\]
Si se conoce la cantidad de armadura longitudinal y de cortante, podemos definir el ángulo θ mediante la expresión
\[{{\tan }^{2}}\theta =\frac{\frac{{{A}_{sw}}{{f}_{ywd}}}{s}}{\frac{{{A}_{sl}}{{f}_{yd}}}{{{u}_{k}}}}\]
SustituyendoTRd,s obtenemos
\[{{T}_{Rd,s}}=2{{A}_{k}}\sqrt{\frac{{{A}_{sw}}}{s}{{f}_{ywd~}}\frac{{{A}_{sl}}}{{{u}_{k}}}~{{f}_{yd}}}\]
Donde
Asw área de refuerzo para esfuerzo cortante
s es la separación radial de los estribos del refuerzo para esfuerzo cortante
fywd es la resistencia efectiva de diseño del refuerzo para esfuerzo cortante
Asl área de refuerzo longitudinal
uk es la circunferencia exterior de la sección transversal
fywd es la resistencia efectiva de cálculo de la armadura longitudinal
La fuerza en la armadura longitudinal puede deducirse de La fuerza cortante en un muro de una sección sometida a un momento torsor puro, que se da como:
\[V=\frac{{{T}_{Ed}}}{2{{A}_{k}}}{{u}_{k}}\]
Esa fuerza se transforma a la dirección longitudinal y obtenemos:
\[{{F}_{l}}=\frac{{{T}_{Ed}}{{u}_{k}}}{2{{A}_{k}}~\tan \theta }\]
El intervalo permitido de los valores del ángulo θ es similar al del control de cizalladura, es decir, 1 < cot θ < 2,5. La dependencia entre resistencias puede verse en la Fig. siguiente. El diagrama muestra que al aumentar el ángulo θ la resistenciaTRd,max es creciente, la resistenciaTRd.s es decreciente y la resistenciaTRd,c es constante, ya que no se basa en el método de analogía de cerchas.
\[ \textsf{\textit{\footnotesize{qquad Závislost únosnosti průřezu v kroucení na úhlu θ.}}]
Cálculo de las características de la sección transversal para la torsión
Para comprobar la sección transversal para la torsión es necesario establecer una denominada sección cerrada de pared delgada equivalente. En la determinación de las dimensiones de la sección transversal de pared delgada equivalente suponiendo una forma rectangular.Para el área real de los estados rectangulares A = b×h y para la circunferencia del rectángulo u =2 (b +h).El uso de estas dos ecuaciones puede proporcionar alternativa área de forma rectangular delgada y la periferia de la sección transversal original. Resolver dos ecuaciones con dos incógnitas que obtenemos:
\[b=\frac{-u\pm \sqrt{{{u}^{2}}-16A}}{-4}\text{ }\!\!~\!\!\text{ }]
\[h=\frac {\left( u-2\text{b} \right)}{2}]
El espesor de pared de la sección transversal efectiva puede definirse a partir de la periferia y el área de la sección como:
\[t=\text{A}/\text{u}\]
A continuación, el área y la periferia definida por la línea central de la sección transversal efectiva:
\[{A}_{k}=left( \text{h}-\text{t} \right)\text{ }\!\!~\!\!\text{ }left( \text{b}-\text{t} \right)\text{ }\!\!~\!\!\text{ }]
\[{{u}_{k}}=2\left( \left( \text{h}-\text{t} \right)+\text{ }\!\!~\!\!\text{ }\left( \text{b}-\text{t} \right) \right)\]
El problema con este método es para la sección transversal de tipo T con una placa ancha cuando se toma el área total y la periferia para calcular las dimensiones (incluyendo esta placa).En las futuras versiones del programa IDEA RCS se habilitará la selección de la parte de la sección transversal más maciza, que se utilizará para comprobar la torsión.