General introduction for the structural design of concrete details
The design and assessment of concrete elements are normally performed at the sectional (1D-element) or point (2D-element) level. This procedure is described in all standards for structural design, e.g., in (EN 1992-1-1 or ACI 318-19), and it is used in everyday structural engineering practice. However, it is not always known or respected that the procedure is only acceptable in areas where the Bernoulli-Navier hypothesis of plane strain distribution applies (referred to as B-regions). The places where this hypothesis does not apply are called discontinuity or disturbed regions (D-Regions). Examples of B and D regions of 1D-elements are given in (Fig. 1). These are, e.g., bearing areas, parts where concentrated loads are applied, locations where an abrupt change in the cross-section occurs, openings, etc. When designing concrete structures, we meet a lot of other D-Regions such as walls, bridge diaphragms, corbels, etc.
\[ \textsf{\textit{\footnotesize{Fig. 1\qquad Discontinuity regions (Navrátil et al. 2017)}}}\]
In the past, semi-empirical design rules were used for dimensioning discontinuity regions. Fortunately, these rules have been largely superseded over the past decades by strut-and-tie models (Schlaich et al., 1987) and stress fields (Marti 1985), which are featured in current design codes and frequently used by designers today. These models are mechanically consistent and powerful tools. Note that stress fields can generally be continuous or discontinuous and that strut-and-tie models are a special case of discontinuous stress fields.
Despite the evolution of computational tools over the past decades, Strut-and-Tie models are essentially still used as hand calculations. Their application for real-world structures is tedious and time-consuming since iterations are required, and several load cases need to be considered. Furthermore, this method is not suitable for verifying serviceability criteria (deformations, crack widths, etc.).
The interest of structural engineers in a reliable and fast tool to design D-regions led to the decision to develop the new Compatible Stress Field Method, a method for computer-aided stress field design that allows the automatic design and assessment of structural concrete members subjected to in-plane loading.
The Compatible Stress Field Method (CSFM) is a continuous FE-based stress field analysis method in which classic stress field solutions are complemented with kinematic considerations, i.e., the state of strain is evaluated throughout the structure. Hence, the effective compressive strength of concrete can be automatically computed based on the state of transverse strain in a similar manner as in compression field analyses that account for compression softening (Vecchio and Collins 1986; Kaufmann and Marti 1998) and the EPSF method (Fernández Ruiz and Muttoni 2007). Moreover, the CSFM considers tension stiffening, providing realistic stiffnesses to the elements, and covers all design code prescriptions (including serviceability and deformation capacity aspects) not consistently addressed by previous approaches. The CSFM uses common uniaxial constitutive laws provided by design standards for concrete and reinforcement. These are known at the design stage, which allows the partial safety factor method to be used. Hence, designers do not have to provide additional, often arbitrary material properties as are typically required for non-linear FE-analyses, making the method perfectly suitable for engineering practice.
To foster the use of computer-aided stress fields by structural engineers, these methods should be implemented in user-friendly software environments. To this end, the CSFM has been implemented in IDEA StatiCa Detail; a new user-friendly commercial software developed jointly by ETH Zurich and the software company IDEA StatiCa in the framework of the DR-Design Eurostars-10571 project.
Design tools for reinforcement
Workflow and goals
The goal of reinforcement design tools in the CSFM is to help designers determine the location and required amount of reinforcing bars efficiently. The following tools are available to help / guide the user in this process: linear calculation and topology optimization.
Reinforcement design tools consider more simplified constitutive models than the models used for the final verification of the structure. Therefore, the definition of the reinforcement in this step should be considered a pre-design to be confirmed/refined during the final verification step. The use of the different reinforcement design tools will be depicted in the model shown in Fig. 3, which consists of one end of a simply supported beam with variable depth subjected to a uniformly distributed load.
\[ \textsf{\textit{\footnotesize{Fig. 3\qquad Model used to illustrate the use of the reinforcement design tools.}}}\]
Linear analysis
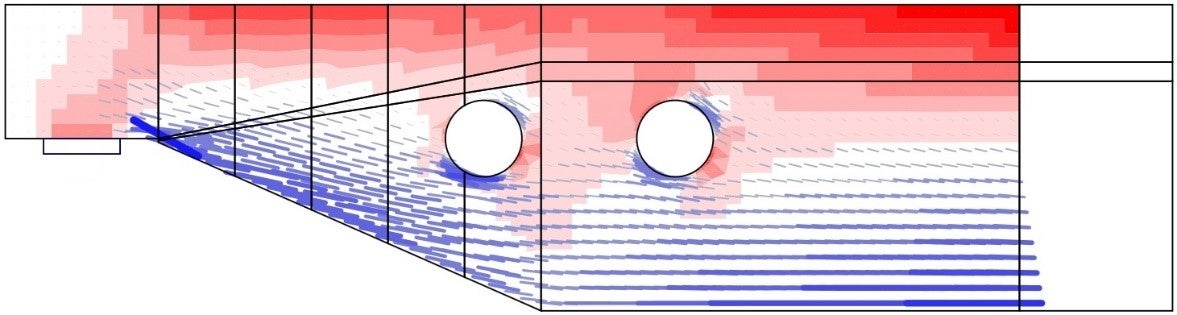
The linear analysis considers linear elastic material properties and neglects reinforcement in the concrete region. It is, therefore, a very fast calculation that provides a first insight into the locations of tension and compression areas. An example of such a calculation is shown in Fig. 4.
\[ \textsf{\textit{\footnotesize{Fig. 4\qquad Results from the linear analysis tool for defining reinforcement layout}}}\]
\[ \textsf{\textit{\footnotesize{(red: areas in compression, blue: areas in tension).}}}\]
Topology optimization
Topology optimization is a method that aims to find the optimal distribution of material in a given volume for a certain load configuration. The topology optimization implemented in Idea StatiCa Detail uses a linear finite element model. Each finite element may have a relative density from 0 to 100 %, representing the relative amount of material used. These element densities are the optimization parameters in the optimization problem. The resulting material distribution is considered optimal for the given set of loads if it minimizes the total strain energy of the system. By definition, the optimal distribution is also the geometry that has the largest possible stiffness for the given loads.
The iterative optimization process starts with a homogeneous density distribution. The calculation is performed for multiple total volume fractions (20%, 40%, 60%, and 80%), which allows the user to select the most practical result. The resulting shape consists of trusses with struts and ties and represents the optimum shape for the given load cases (Fig. 5).
\[ \textsf{\textit{\footnotesize{Fig. 5\qquad Results from the topology optimization design tool with 20\% and 40\% effective volume}}}\]
\[ \textsf{\textit{\footnotesize{(red: areas in compression, blue: areas in tension).}}}\]
Introducción a la aplicación de elementos finitos
El CSFM considera campos de tensión continuos en el hormigón (elementos finitos 2D), complementados por elementos discretos de "varilla" que representan la armadura (elementos finitos 1D). Por lo tanto, la armadura no se incrusta difusamente en los elementos finitos 2D del hormigón, sino que se modela explícitamente y se conecta a ellos. En el modelo de cálculo se considera un estado de tensiones plano.
\[ \textsf{\textit{footnotesize{Fig. 6\qquad Visualización del modelo de cálculo de un elemento estructural (viga recortada) en Idea StatiCa Detail.}}]
Se pueden modelizar tanto muros y vigas enteras, como detalles (partes) de vigas (región de discontinuidad aislada, también llamada extremo recortado). En el caso de muros y vigas enteras, los apoyos deben definirse de tal manera que resulte una estructura (externamente) isostática (estáticamente determinada) o hiperestática (estáticamente indeterminada). La transferencia de carga en los extremos recortados de las vigas se introduce mediante una zona de transferencia especial de Saint-Venant, que garantiza una distribución de tensiones realista en la región de detalle analizada.
Estados límite y cálculo de la anchura de fisura
La evaluación de la estructura utilizando el CSFM se realiza mediante dos análisis diferentes: uno para la capacidad de servicio y otro para las combinaciones de carga de los estados límite últimos. El análisis de capacidad de servicio asume que el comportamiento último del elemento es satisfactorio y que las condiciones de fluencia del material no se alcanzarán en los niveles de carga de capacidad de servicio. Este enfoque permite el uso de modelos constitutivos simplificados (con una rama lineal del diagrama tensión-deformación del hormigón) para el análisis de capacidad de servicio con el fin de mejorar la estabilidad numérica y la velocidad de cálculo. Por lo tanto, se recomienda utilizar el flujo de trabajo que se presenta a continuación, en el que el análisis del estado límite último se lleva a cabo como primer paso.
Análisis del estado límite último
Las diferentes verificaciones exigidas por los códigos de diseño específicos se evalúan a partir de los resultados directos proporcionados por el modelo. Las verificaciones ULS se llevan a cabo para la resistencia del hormigón, la resistencia de la armadura y el anclaje (tensiones de cizalladura de unión).
Para garantizar que un elemento estructural tiene un diseño eficiente, es muy recomendable ejecutar un análisis preliminar que tenga en cuenta los siguientes pasos:
- Elegir una selección de las combinaciones de carga más críticas.
- Calcular sólo las combinaciones de carga de Estado Límite Último (ELU).
- Utilice una malla gruesa (aumentando el multiplicador del tamaño de malla por defecto en Configuración (Fig. 19)).
\[ \textsf{\textit{footnotesize{Fig. 19\qquad Multiplicador de malla.}}]
Dicho modelo se calculará muy rápidamente, permitiendo a los diseñadores revisar el detallado del elemento estructural de manera eficiente y volver a ejecutar el análisis hasta que se cumplan todos los requisitos de verificación para las combinaciones de carga más críticas. Una vez cumplidos todos los requisitos de verificación de este análisis preliminar, se sugiere incluir todas las combinaciones de carga última y utilizar un tamaño de malla fino (el tamaño de malla recomendado por el programa). El usuario puede cambiar el tamaño de malla mediante el multiplicador, que puede alcanzar valores de 0,5 a 5 (Fig. 19).
Los resultados básicos y las verificaciones (tensión, deformación y utilización (es decir, el valor calculado/valor límite del código), así como la dirección de las tensiones principales en el caso de elementos de hormigón) se muestran mediante diferentes gráficos donde la compresión se presenta generalmente en rojo y la tensión en azul. Pueden resaltarse los valores máximos y mínimos globales de toda la estructura, así como los valores máximos y mínimos de cada parte definida por el usuario. En una pestaña separada del programa, pueden mostrarse resultados avanzados como los valores de los tensores, las deformaciones de la estructura y las relaciones de armadura (efectiva y geométrica) utilizadas para calcular la rigidez a tracción de las barras de armadura. Además, pueden presentarse las cargas y reacciones para combinaciones o casos de carga seleccionados.
Análisis de los estados límite de servicio
Se realizan evaluaciones de los estados límite de servicio para la limitación de tensiones, la anchura de las fisuras y los límites de deformación. Las tensiones se comprueban en el hormigón y los elementos de refuerzo de acuerdo con el código aplicable de forma similar a la especificada para el ULS.
El análisis de capacidad de servicio contiene ciertas simplificaciones de los modelos constitutivos que se utilizan para el análisis de los estados límite últimos. Se supone una adherencia perfecta, es decir, la longitud de anclaje no se verifica en servicio. Además, no se tiene en cuenta la rama plástica de la curva tensión-deformación del hormigón en compresión, mientras que la rama elástica es lineal e infinita. Estas simplificaciones mejoran la estabilidad numérica y la velocidad de cálculo, y no reducen la generalidad de la solución siempre que los límites de tensión del material resultantes en servicio estén claramente por debajo de sus límites elásticos (como exigen las normas). Por lo tanto, los modelos simplificados utilizados para la aptitud para el servicio sólo son válidos si se cumplen todos los requisitos de verificación.
Cálculo de la anchura de la grieta y refuerzo por tracción
Cálculo de la anchura de la grieta
Existen dos formas de calcular la anchura de las fisuras: fisuración estabilizada y no estabilizada. En función de la relación geométrica de armadura en cada parte de la estructura se decide, qué tipo de modelo de cálculo de fisuración se utilizará (TCM para fisuración estabilizada y POM para modelo de fisuración no estabilizada).
\( \textsf{\textit{footnotesize{Fig. 20 \qquad Cálculo del ancho de fisura: (a) cinemática de la fisura considerada; (b) proyección de la cinemática de la fisura en la principal}}) \(c) anchura de fisura en la dirección de la barra de armadura para fisuración estabilizada; (d) casos con fisuración estabilizada. \( \textsf{textit{footnotesize{fisuración local no estabilizada independientemente de la cantidad de armadura; (e) ancho de fisura en la dirección de la barra de armadura}})\( \textsf{textit{footnotesize{para fisuración no estabilizada.}})
Mientras que el CSFM proporciona un resultado directo para la mayoría de las comprobaciones (por ejemplo, capacidad de la barra, flechas...), los resultados de la anchura de fisura se calculan a partir de los resultados de la deformación de la armadura proporcionados directamente por el análisis de EF siguiendo la metodología descrita en la Fig. 20. Se considera una cinemática de fisura sin deslizamiento (apertura de fisura pura) (Fig. 20a), que es coherente con los principales supuestos del modelo. Las direcciones principales de las tensiones y deformaciones definen la inclinación de las grietas (θr = θs=θe). De acuerdo con (Fig. 20b), la anchura de la grieta(w) puede proyectarse en la dirección de la barra de refuerzo(wb), lo que conduce a:
\[w = \frac{w_b}{cos\left(θ_r + θ_b - \frac{π}{2}\right)}\].
donde θb es la inclinación de la barra.
Tenga en cuenta, que el programa muestra los valores de θr y θb < π/2. Significa que la ecuación anterior funciona para los casos, donde la armadura y la grieta pasan por los diferentes cuadrantes del sistema de coordenadas cartesianas como se muestra en la Fig. 20, donde la armadura pasa por I. y III. cuadrantes y la grieta por II y IV. Para los casos en que la armadura y la fisura atraviesan los mismos cuadrantes, la ecuación debe modificarse como sigue:
\[w = \frac{w_b}{coscos\left(-θ_r + θ_b + \frac{π}{2}\right)}\].
La componente wb se calcula de forma coherente a partir de los modelos de rigidización a tracción mediante la integración de las deformaciones de la armadura. Para aquellas regiones con patrones de grietas completamente desarrollados, las deformaciones medias calculadas (em) a lo largo de las barras de refuerzo se integran directamente a lo largo de la separación de grietas(sr), como se indica en (Fig. 20c). Aunque este enfoque para calcular las direcciones de las fisuras no se corresponde con la posición real de las fisuras, proporciona valores representativos que conducen a resultados de anchura de fisura que pueden compararse con los valores de anchura de fisura requeridos por el código en la posición de la barra de refuerzo.
Se observan situaciones especiales en las esquinas cóncavas de la estructura calculada. En este caso, la esquina predetermina la posición de una única grieta que se comporta de forma no estabilizada antes de que se desarrollen grietas adyacentes adicionales. Estas grietas adicionales se desarrollan generalmente después del rango de serviciabilidad (Mata-Falcón 2015), lo que justifica el cálculo de los anchos de grieta en dicha región como si fueran no estabilizadas (Fig. 21).
\[ \textsf{\textit{footnotesize{Fig. 21\qquad Definición de la región en esquinas cóncavas en la que se calcula el ancho de fisura como si fuera no estabilizada.}}]
Rigidización por tensión
La aplicación de la rigidización a tracción distingue entre los casos de fisuras estabilizadas y no estabilizadas. En ambos casos, el hormigón se considera completamente agrietado antes de la carga por defecto.
\( \textsf{\textit{footnotesize{Fig. 22\qquad Modelo de rigidización por tracción: (a) elemento de cordón de tracción para fisuración estabilizada con distribución de cortante de adherencia,}}}) \tensiones del acero y del hormigón, y deformaciones del acero entre fisuras, considerando la separación media entre fisuras; (b) hipótesis de arrancamiento}}) \para fisuración no estabilizada con distribución de tensiones y deformaciones de acero y de cizalladura de adherencia alrededor de la fisura; (c) resultante}}) \Comportamiento del cordón de tracción en términos de tensiones de armadura en las fisuras y deformaciones medias para el acero europeo B500B. \(d) Detalle de las ramas iniciales de la respuesta del cordón de tracción.
Fisuración estabilizada
En patrones de grieta completamente desarrollados, la rigidización por tensión se introduce utilizando el Modelo de Cuerda de Tensión (TCM) (Marti et al. 1998; Alvarez 1998) - Fig. 22a - que ha demostrado dar excelentes predicciones de respuesta a pesar de su simplicidad (Burns 2012). El TCM asume una relación de esfuerzo cortante de adherencia escalonada, rígida-perfectamente plástica con τb= τb0 =2 fctm para σs ≤ fy y τb =τb1 = fctm para σs> fy. Tratando cada barra de refuerzo como una cuerda de tracción - Fig. 22b y Fig. 22a - se puede determinar la distribución de las tensiones de cortante de enlace, del acero y del hormigón y, por tanto, la distribución de tensiones entre dos fisuras para cualquier valor dado de las tensiones (o deformaciones) máximas del acero en las fisuras.
Parasr = sr0, puede formarse o no una nueva grieta porque en el centro entre dos grietas σc1 = fct. En consecuencia, la separación entre grietas puede variar en un factor de dos, es decir,sr = λsr0, con l = 0,5...1,0. Suponiendo un valor determinado de λ, la deformación media de la cuerda (εm) puede expresarse en función de las tensiones máximas de la armadura (es decir, las tensiones en las fisuras, σsr). Para el diagrama de tensión-deformación bilineal idealizado para las barras desnudas de refuerzo consideradas por defecto en el CSFM, se obtienen las siguientes expresiones analíticas de forma cerrada (Marti et al. 1998):
\[\varepsilon_m = \frac{\sigma_{sr}}{E_s} - \frac{\tau_{b0}s_r}{E_s Ø}\].
\textrm{for}qquad\qquad\sigma_{sr} \le f_y\]
\{\varepsilon_m} = {\frac{{{{\left( {{sigma_{sr}} - {f_y}} \right)}^2}Ø}}{4{E_{sh}}{\tau _{b1}}{s_r}}left( {1 - \frac{{E_{sh}{tau_{b0}}}}{{E_s}{tau_{b1}}}}} \right) + \frac{{left( {{sigma_{sr}} - {f_y}} \right)}}{{E_s}{frac{{{tau_{b0}}}}{{\tau_{b1}}}} + \left( {{{varepsilon_y}} - \frac{{\tau_{b0}} {{s_r}} {{E_s}Ø}} {right)}]
\[\textrm{for}\qquad\qquad{f_y} \...es decir, a la izquierda... \izquierda( {{f_y} + \frac{2{\tau _{b1}}{s_r}}Ø} {derecha)\]
\[ \varepsilon_m = \frac{f_s}{E_s} + \frac{\sigma_{sr}-f_y}{E_{sh}} - \frac{tau_{b1} s_r}{E_{sh} Ø}\]
\izquierda(f_y + \frac{2\tau_{b1}s_r} {Ø}derecha) \le \sigma_{sr}} \f_t\]
donde:
Esh el módulo de endurecimiento del aceroEsh =(ft - fy)/(εu - fy /Es) ,
Es el módulo de elasticidad de la armadura,
Ø diámetro de la barra de refuerzo,
sr distancia entre fisuras ,
σsr tensiones de la armadura en las fisuras,
σs tensiones reales de la armadura,
fy límiteelástico de la armadura.
La implementación de Idea StatiCa Detail del CSFM considera por defecto la separación media entre fisuras al realizar el análisis del campo de tensiones asistido por ordenador. Se considera que la separación media de fisuras es 2/3 de la separación máxima de fisuras (λ = 0,67), lo que sigue las recomendaciones realizadas a partir de ensayos de flexión y tracción (Broms 1965; Beeby 1979; Meier 1983). Cabe señalar que en los cálculos de la anchura de las grietas se considera una separación máxima entre grietas (λ = 1,0) para obtener valores conservadores.
La aplicación del MTC depende de la relación de armadura, por lo que es crucial la asignación a cada barra de armadura de una superficie de hormigón adecuada que actúe a tracción entre las fisuras. Se ha desarrollado un procedimiento numérico automático para definir la correspondiente relación de armadura efectiva (ρeff = As/Ac,eff) para cualquier configuración, incluida la armadura sesgada (Fig. 23).
\( \textsf{\textit{footnotesize{Fig. 23\qquad Área efectiva de hormigón en tensión para fisuración estabilizada: (a) área máxima de hormigón que puede activarse;}}}) \(b) cubierta y condición de simetría global; (c) área efectiva resultante.
Agrietamiento no estabilizado
Las fisuras existentes en regiones con relaciones geométricas de armadura inferiores a ρcr, es decir, la cantidad mínima de armadura para la que ésta es capaz de soportar la carga de fisuración sin ceder, se generan por acciones no mecánicas (por ejemplo, retracción) o por la progresión de fisuras controladas por otras armaduras. El valor de esta armadura mínima se obtiene de la siguiente manera:
\[{\rho _{cr}} = \frac{{f_{ct}}}}}{{{f_y}} - \left( {n - 1} \right){f_{ct}}}}}]
donde:
fy límite elástico de la armadura,
fct resistencia a la tracción del hormigón,
n relación modular, n =Es /Ec.
Para el hormigón convencional y el acero de armadura, ρcr asciende aproximadamente al 0,6%.
Para estribos con relaciones de armadura inferiores a ρcr, la fisuración se considera no estabilizada y la rigidización a tracción se implementa mediante el Modelo Pull-Out (POM) descrito en la Fig. 22b. Este modelo analiza el comportamiento de una única fisura considerando que no hay interacción mecánica entre fisuras separadas, despreciando la deformabilidad del hormigón a tracción y asumiendo la misma relación escalonada, rígida-perfectamente plástica de esfuerzo cortante de adherencia-deslizamiento utilizada por el MTC. Esto permite obtener la distribución de la deformación de la armadura (εs) en las proximidades de la fisura para cualquier tensión máxima del acero en la fisura (σsr) directamente a partir del equilibrio. Dado que se desconoce el espaciado de la fisura para un patrón de fisura no completamente desarrollado, la deformación media (εm) se calcula para cualquier nivel de carga sobre la distancia entre puntos con deslizamiento cero cuando la barra de refuerzo alcanza su resistencia a tracción(ft) en la fisura(lε,avg en Fig. 22b), dando lugar a las siguientes relaciones:
Los modelos propuestos permiten calcular el comportamiento de la armadura adherida, que finalmente se considera en el análisis. Este comportamiento (incluyendo la rigidización a tracción) para la armadura europea más común (B500B, conft / fy = 1,08 y εu = 5%) se ilustra en la Fig. 22c-d.
Structural element checks according to Eurocode
Assessment of the structure using the CSFM is performed by two different analyses: one for serviceability, and one for ultimate limit state load combinations. The serviceability analysis assumes that the ultimate behavior of the element is satisfactory, and the yield conditions of the material will not be reached at serviceability load levels. This approach enables the use of simplified constitutive models (with a linear branch of concrete stress-strain diagram) for serviceability analysis to enhance numerical stability and calculation speed.
References
ACI Committee 318. 2009a. Building Code Requirements for Structural Concrete (ACI 318-08) and Commentary. Farmington Hills, MI: American Concrete Institute.
Alvarez, Manuel. 1998. Einfluss des Verbundverhaltens auf das Verformungsvermögen von Stahlbeton. IBK Bericht 236. Basel: Institut für Baustatik und Konstruktion, ETH Zurich, Birkhäuser Verlag.
Beeby, A. W. 1979. “The Prediction of Crack Widths in Hardened Concrete.” The Structural Engineer 57A (1): 9–17.
Broms, Bengt B. 1965. “Crack Width and Crack Spacing In Reinforced Concrete Members.” ACI Journal Proceedings 62 (10): 1237–56. https://doi.org/10.14359/7742.
Burns, C.. 2012. “Serviceability Analysis of Reinforced Concrete Members Based on the Tension Chord Model.” IBK Report Nr. 342, Zurich, Switzerland: ETH Zurich.
Crisfield, M. A. 1997. Non-Linear Finite Element Analysis of Solids and Structures. Wiley.
European Committee for Standardization (CEN). 2015. 1 Eurocode 2: Design of concrete structures - Part 1-1: General rules and rules for buildings. Brussels: CEN, 2005.
Fernández Ruiz, M., and A. Muttoni. 2007. “On Development of Suitable Stress Fields for Structural Concrete.” ACI Structural Journal 104 (4): 495–502.
Kaufmann, W., J. Mata-Falcón, M. Weber, T. Galkovski, D. Thong Tran, J. Kabelac, M. Konecny, J. Navratil, M. Cihal, and P. Komarkova. 2020. “Compatible Stress Field Design Of Structural Concrete. Berlin, Germany.”AZ Druck und Datentechnik GmbH, ISBN 978-3-906916-95-8.
Kaufmann, W., and P. Marti. 1998. “Structural Concrete: Cracked Membrane Model.” Journal of Structural Engineering 124 (12): 1467–75. https://doi.org/10.1061/(ASCE)0733-9445(1998)124:12(1467).
Kaufmann, W.. 1998. “Strength and Deformations of Structural Concrete Subjected to In-Plane Shear and Normal Forces.” Doctoral dissertation, Basel: Institut für Baustatik und Konstruktion, ETH Zürich. https://doi.org/10.1007/978-3-0348-7612-4.
Konečný, M., J. Kabeláč, and J. Navrátil. 2017. Use of Topology Optimization in Concrete Reinforcement Design. 24. Czech Concrete Days (2017). ČBS ČSSI. https://resources.ideastatica.com/Content/06_Detail/Verification/Articles/Topology_optimization_US.pdf.
Marti, P. 1985. “Truss Models in Detailing.” Concrete International 7 (12): 66–73.
Marti, P. 2013. Theory of Structures: Fundamentals, Framed Structures, Plates and Shells. First edition. Berlin, Germany: Wiley Ernst & Sohn.
http://sfx.ethz.ch/sfx_locater?sid=ALEPH:EBI01&genre=book&isbn=9783433029916.
Marti, P., M.Alvarez, W. Kaufmann, and V. Sigrist. 1998. “Tension Chord Model for Structural Concrete.” Structural Engineering International 8 (4): 287–298.
https://doi.org/10.2749/101686698780488875.
Mata-Falcón, J. 2015. “Serviceability and Ultimate Behaviour of Dapped-End Beams (In Spanish: Estudio Del Comportamiento En Servicio y Rotura de Los Apoyos a Media Madera).” PhD thesis, Valencia: Universitat Politècnica de València.
Meier, H. 1983. “Berücksichtigung Des Wirklichkeitsnahen Werkstoffverhaltens Beim Standsicherheitsnachweis Turmartiger Stahlbetonbauwerke.” Institut für Massivbau, Universität Stuttgart.
Navrátil, J., P. Ševčík, L. Michalčík, P. Foltyn, and J. Kabeláč. 2017. A Solution for Walls and Details of Concrete Structures. 24. Czech Concrete Days.
Schlaich, J., K. Schäfer, and M. Jennewein. 1987a. “Toward a Consistent Design of Structural Concrete.” PCI Journal 32 (3): 74–150.
Vecchio, F.J., and M.P. Collins. 1986. “The Modified Compression Field Theory for Reinforced Concrete Elements Subjected to Shear.” ACI Journal 83 (2): 219–31.