Soldadura de filete en junta solapada

Descripción

El objetivo de este capítulo es la verificación del método de elementos finitos basado en componentes (CBFEM) de una soldadura de filete en una junta solapada con el método de componentes (CM). Dos placas están conectadas en tres configuraciones, a saber, con una soldadura transversal, con una soldadura longitudinal, y una combinación de soldaduras transversales y longitudinales. La longitud y el espesor de garganta de la soldadura son los parámetros variables en el estudio. El estudio también cubre soldaduras largas cuya resistencia se reduce debido a la concentración de tensiones. La junta está cargada por una fuerza normal.

Modelo analítico

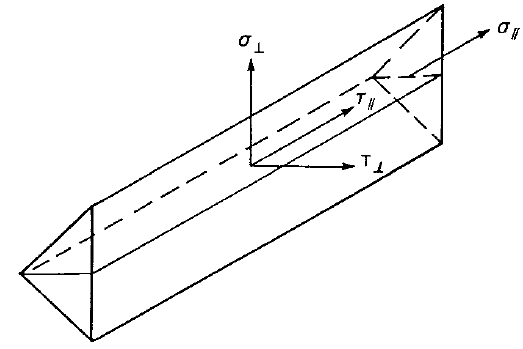
La soldadura de filete es el único componente examinado en el estudio. Las soldaduras están diseñadas para ser el componente más débil en la junta. La soldadura está diseñada según EN 1993-1-8:2005. La resistencia de diseño de la soldadura de filete se determina utilizando el método Direccional dado en Cl. 4.5.3.2 en EN 1993-1-8:2005. Los métodos de cálculo disponibles para verificar la resistencia de las soldaduras de filete se basan en la suposición simplificadora de que las tensiones se distribuyen uniformemente dentro de una sección de garganta de una soldadura de filete, llevando a las tensiones normales y tensiones de corte mostradas en Fig. 4.1.1, como sigue:

• σ_⊥ es la tensión normal perpendicular a la sección de garganta;
• σ_∥ es la tensión normal paralela al eje de la soldadura en su sección transversal;
• τ_⊥ es la tensión de corte (en el plano de la sección de garganta) perpendicular al eje de la soldadura;
• τ_∥ es la tensión de corte (en el plano de la sección de garganta) paralela al eje de la soldadura.

La tensión normal σ_∥ paralela al eje no se considera al verificar la resistencia de diseño de una soldadura.

\[ \textsf{\textit{\footnotesize{Fig. 4.1.1 Tensiones en una sección de garganta de una soldadura de filete}}}\]

La resistencia de diseño de la soldadura de filete será suficiente si se satisfacen ambas condiciones siguientes:

\[ \sqrt{\sigma_{\perp}^2 + 3 \cdot ( \tau_{\perp}^2 + \tau_{\perp}^2 )} \le \frac{f_\textrm{u}}{\beta_\textrm{w} \gamma_\textrm{M2}} \]

\[ \sigma_{\perp} \le \frac{0.9 f_\textrm{u}}{\gamma_\textrm{M2}} \]

En juntas solapadas más largas que \( 150 \cdot a \), el factor de reducción \(\beta_{\mathrm{Lw,1}}\) está dado por:

\( \beta_{\mathrm{Lw,1}} = 1.2 - \frac{0.2 L_\textrm{j}}{150 a} \)  pero   \(\beta_{\mathrm{Lw,1}} \le 1.0 \)

Modelo numérico

El componente de soldadura en CBFEM se describe en Fundamentos teóricos generales y Fundamentos teóricos EN. Se utiliza material elástico-plástico no lineal para las soldaduras en este estudio. La deformación plástica límite se alcanza en la parte más larga de la soldadura, y los picos de tensión se redistribuyen.

Verificación de resistencia

Se proporciona una visión general de los ejemplos considerados y las propiedades del material en Tab. 4.1.1. Las configuraciones de soldadura son T para transversal, P para soldadura paralela, y TP para una combinación de ambas; ver la geometría en Fig. 4.1.2. El grado de acero fue S235 (f_y = 235 MPa, f_u = 360 MPa, E = 210 GPa, β_w = 0,8). Los factores de seguridad parciales fueron γ_M0 = 1.0, γ_M2 = 1.25. La geometría del modelo se muestra en Fig. 4.1.2. Las placas tienen un espesor de 20 mm. La conexión es simétrica, y la placa se extrae de la conexión de empalme soldada. La longitud y anchura de las placas se ajustan según la longitud de la soldadura paralela y transversal. La resistencia de la soldadura es siempre el modo de falla gobernante. El espesor de garganta de la soldadura es de 3 mm. Las longitudes de las soldaduras transversales y paralelas varían en este estudio paramétrico.

\[ \textsf{\textit{\footnotesize{Dibujo 4.1 Geometría de la junta con dimensiones}}}\]

La resistencia de diseño de la soldadura calculada por CBFEM se compara con los resultados de CM. Los resultados se presentan en Tab. 4.1.1 – 4.1.3 y Fig. 4.1.3 – 4.1.5.

\[ \textsf{\textit{\footnotesize{Fig.4.1.2 Geometría del espécimen}}}\]

Cálculo de resistencia de soldaduras transversales 

\[\sqrt{ \sigma_{\perp}^2 + 3 \cdot \left( \tau_{\perp}^2 + \tau_{\parallel}^2\right)} \leq \frac{f_\textrm{u}}{\beta_{\textrm{w}} \cdot \gamma_{\textrm{M2}}}\]

\[\sigma_{\perp} = \tau_{\perp} = \frac{\sigma_\textrm{N}}{\sqrt{2}} = \frac{N}{L_{\textrm{t}} \cdot a}\cdot \frac{1}{\sqrt{2}} \]

\[ \tau_{\parallel} = 0\]

\[ \sqrt{ \left( \frac{\sigma_\textrm{N}}{\sqrt{2}} \right)^2 + 3 \cdot \left( \frac{\sigma_\textrm{N}}{\sqrt{2}} \right)^2} \leq \frac{f_\textrm{u}}{\beta_{\textrm{w}} \cdot \gamma_{\textrm{M2}}}\]

\[ \sqrt{ \left( \frac{N}{L_{\textrm{t}}\cdot a}\cdot \frac{1}{\sqrt{2}} \right)^2 + 3 \cdot \left( \frac{N}{L_{\textrm{t}}\cdot a}\cdot \frac{1}{\sqrt{2}} \right)^2} \leq \frac{f_\textrm{u}}{\beta_{\textrm{w}} \cdot \gamma_{\textrm{M2}}}\]

\[ N \leq \frac{f_\textrm{u} \cdot L_{\textrm{t}}\cdot a }{\beta_{\textrm{w}}  \cdot  \gamma_{\textrm{M2}}  \cdot  \sqrt{2}} \]

\[ \sigma_{\perp}= \frac{N}{L_{\textrm{t}} \cdot a}\cdot \frac{1}{\sqrt{2}} \leq \frac{f_\textrm{u}  \cdot  0.9}{ \gamma_{\textrm{M2}}} \]

\[ N \leq \frac{f_{u}  \cdot L_{\textrm{t}}\cdot  a  \cdot  0.9  \cdot  \sqrt{2}}{ \gamma_{\textrm{M2}} }   \]

Donde:

\(a\) - espesor de garganta de soldadura

\(N\) - la fuerza normal que actúa sobre la viga

\(L_{\textrm{t}}\) - longitud total de soldadura transversal 

\(\beta_{\mathrm{w}}\) - factor de correlación tomado de EN 1993-1-8 Tabla 4.1

\(f_\textrm{u}\) - resistencia nominal última a la tracción de la parte más débil unida

\(\gamma_{\mathrm{M2}}\) - factor de seguridad parcial para soldaduras

Cálculo de resistencia de soldadura paralela

\[\sqrt{ \sigma_{\perp}^2 + 3 \cdot \left( \tau_{\perp}^2 + \tau_{\parallel}^2\right)} \leq\frac{f_\textrm{u}}{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}}}\]

\[\sigma_{\perp} = \tau_{\perp} = 0 \]

\[ \tau_{\parallel} = \frac{V}{L_{\textrm{p}}  \cdot  a}\]

\[ \sqrt{  3 \cdot \left( \tau_{\parallel} \right)^2} \leq \frac{f_\textrm{u}}{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}}}\]

\[ \sqrt{  3 \cdot \left(  \frac{V}{L_{\textrm{p}} \cdot a}\right)^2} \leq \frac{f_\textrm{u}}{\beta_{\mathrm{w}} \cdot \gamma_{\mathrm{M2}}}\]

\[ V = \frac{f_\textrm{u}  \cdot  L_{\textrm{p}} \cdot  a  \cdot  \beta_{\mathrm{Lw1}}}{\beta_{\mathrm{w}}  \cdot  \gamma_{\mathrm{M2}}  \cdot  \sqrt{3}} \]

Donde:

\(a\) - espesor de garganta de soldadura

\(V\) - fuerza de corte que actúa sobre la viga

\(L_{\textrm{t}}\) - longitud total de soldaduras paralelas

\(\beta_{\mathrm{w}}\) - factor de correlación tomado de EN 1993-1-8 Tabla 4.1

\(\beta_{\mathrm{Lw1}}\) - factor de reducción de soldadura larga, EN 1993-1-8 Ecuación 4.9

\(f_\textrm{u}\) - resistencia nominal última a la tracción de la parte más débil unida

\(\gamma_{\mathrm{M2}}\) - factor de seguridad parcial para soldaduras

Cálculo transversal y paralelo 

La resistencia calculada a mano para una combinación de soldadura transversal y paralela es simplemente la suma de las resistencias transversal y paralela derivadas de las ecuaciones anteriores. 

Presentación de Resultados

\[ \textsf{\textit{\footnotesize{Tab. 4.1.1 Resultados de soldaduras paralelas}}}\]

\[ \textsf{\textit{\footnotesize{Fig. 4.1.3 Comparación de resistencias de carga de soldaduras paralelas}}}\]

\[ \textsf{\textit{\footnotesize{Fig. 4.1.3.a Influencia de la longitud de soldadura en la resistencia}}}\]

\[ \textsf{\textit{\footnotesize{Tab. 4.1.2 Soldaduras transversales}}}\]

\[ \textsf{\textit{\footnotesize{Fig. 4.1.4 Comparación de resistencias de carga de soldaduras transversales}}}\]

\[ \textsf{\textit{\footnotesize{Fig. 4.1.4.a Influencia de la longitud de soldadura en la resistencia}}}\]

\[ \textsf{\textit{\footnotesize{Tab.4.1.3 Soldaduras agrupadas}}}\]

\[ \textsf{\textit{\footnotesize{Fig. 4.1.5 Comparación de resistencias de carga del grupo}}}\]

La resistencia de soldaduras paralelas, soldaduras transversales y grupos de soldaduras multi-orientadas es casi idéntica según CM y CBFEM. La mayor diferencia en este estudio es del 6% en resistencia de carga.

Los resultados de CBFEM de soldaduras paralelas son ligeramente conservadores pero comienzan a divergir para soldaduras largas. La reducción de resistencia debido a soldaduras largas no es capturada por CBFEM, pero no se espera que soldaduras más largas que 200×espesor de garganta puedan aparecer en cualquier conexión, y hasta esta longitud, los resultados siguen siendo muy cercanos.

Para soldaduras transversales, CBFEM proporciona resultados muy consistentes con 2–4% mayor resistencia.

Ejemplo de referencia

Entradas

Miembro 1 – Iw60x500

• Soldado de placas con espesor t = 20 mm

• Ancho b = 500 mm

• El alma se remueve por operación de fabricación de Abertura

• Acero S235

Miembro 2 – Placa 20x1000

• Espesor t = 20 mm

• Ancho b = 1000 mm

• Acero S235

• Desplazamiento e_x = –90 mm

Soldadura de filete transversal en ambos lados del Miembro 2

• Espesor de garganta a = 3 mm

• Longitud de soldadura L_t = 100 mm

Soldadura de filete paralela en ambos lados del Miembro 2

• Espesor de garganta a = 3 mm

• Longitud de soldadura L_p = 100 mm

Salida

• Resistencia de diseño en tracción F_Rd = 387 kN (Debe notarse que la resistencia fue calculada usando la función "Parar en deformación límite". Consecuentemente, la resistencia real de CBFEM puede ser marginalmente mayor.)