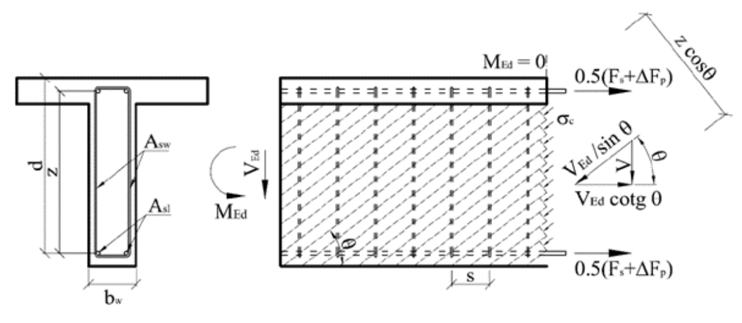
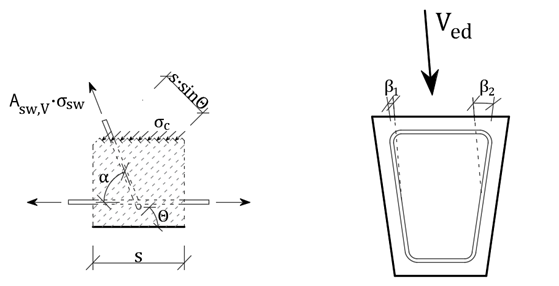
Interacción de la fuerza cortante y la torsión para el refuerzo cortante
Determinación de la fuerza en la armadura de cortante debida al esfuerzo cortante.
El cálculo se basa en la fórmula para calcular la resistencia de la armadura de cortante definida en la norma EN 1992-1-1. Basado en la ecuación 6.13 (cap. 6.2.3 (4)), la resistencia a la carga de un estribo puede obtenerse como:
\[{{V}_{Rd,s}}=\frac{{{A}_{sw,V}}}{s}z{{f}_{ywd}}left( \cot \theta +\cot \alpha \right)\sin \alpha \cos \beta \].
\[\frac{{{A}_{sw,V}}}{s}={{a}_{sw,V}}\]
Asw,V. . . área de la sección transversal de un estribo que resiste el cizallamiento en la sección considerada
s . . . . . espaciado del refuerzo para esfuerzo cortante en la dirección del eje longitudinal del elemento
asw,V. . . área de la sección transversal del refuerzo para esfuerzo cortante por unidad de longitud
z . . . . el brazo de palanca interior. Para un elemento de canto constante, correspondiente al momento flector en el elemento considerado. En el análisis a cortante del hormigón armado sin esfuerzo axil, puede utilizarse normalmente el valor aproximado z = 0,9d.
fywd. . . el límite elástico de cálculo de la armadura de cortante
θ . . . . el ángulo entre el puntal de compresión del hormigón y el eje del elemento perpendicular al esfuerzo cortante
α . . . . . ángulo entre la armadura de cortante y el eje del elemento perpendicular al esfuerzo cortante
β . . . . inclinación de la pata del estribo respecto a la resultante de la fuerza cortante aplicada
La fuerza cortante se redistribuye uniformemente entre las armaduras individuales que resisten la fuerza cortante en función del ángulo de la armadura y de la rigidez axial de las patas individuales del estribo.
\[{{V}_{ed}}={{V}_{ed,1}}+{{V}_{ed,2}}+...+{{V}_{ed,n}}\]
\[{{V}_{ed}={{varepsilon }_{sw,V}}\cdot z\cdot \sum\limits_{i=1}^{{n}_{V}}{{a}_{sw,i,V}}\cdot {{E}_{sw,i,V} {\cdot \left( \cot \theta + {\cot {{alpha }_{i}} \right)\cdot {{cos }^{2}} {{beta }_{i}}]
Además, se puede deducir la deformación media de la armadura considerada en la dirección del esfuerzo cortante resultante:
\[{{\varepsilon }_{sw,V}}=\frac{{{V}_{ed}}}{z\cdot \sum\limits_{i=1}^{{{n}_{V}}}{{{a}_{sw,i,V}}\cdot {{E}_{sw,i,V} {\cdot \left( \cot \theta + {\cot {{alpha }_{i}} \right)\cdot {{cos }^{2}}{{\beta }_i}}}}]
La deformación real de la i-ésima armadura puede calcularse como:
\[{{{varepsilon }_{sw,i,V}}=\frac{{{varepsilon }_{sw,V}} {{sin {{alpha }_{i}}}\cdot \cos {{beta }_{i}}].
La tensión en un tramo dado de la armadura:
\[{{sigma }_{sw,i,V}}= {{varepsilon }_{sw,i,V}}\cdot {{E}_{si,V}}]
Determinación de la fuerza en el estribo individual debida a la torsión
La resistencia a la torsión de una sección puede calcularse a partir de una sección cerrada de pared delgada, en la que el equilibrio se satisface mediante un flujo de cizalladura cerrado. Las secciones sólidas pueden modelarse mediante secciones equivalentes de pared delgada. Para las secciones no macizas, el espesor de pared equivalente no debe superar el espesor de pared real.
El flujo cortante en las paredes de una sección cerrada de pared delgada debido a la torsión puede calcularse como:
\[{{\tau }_{t}}\cdot {{t}_{ef}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\]
La fuerza cortante en una pared particular es entonces:
\{{V}_{i}={\tau }_{t}}\cdot {{t}_{ef}}\cdot {{l}_{i}}]
li. . . . longitud del eje del muro considerado
Fuerza cortante en el alma: la longitud del eje del alma puede sustituirse por el valor del brazo de palanca "z".
\[{{V}_{ed,T}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cdot z\]
Fuerza en los estribos que resiste la torsión por un metro de la longitud del elemento (por unidad de longitud):
\[{{F}_{sw,T}}={frac{{V}_{ed,T}}{z\cdot \cot \theta }={frac{{T}_{ed}}{2{A}_{k}}\cdot tg\theta\]
Descomposiciones de fuerzas para estribo individual
Si se define el mismo material para todos los estribos, el esfuerzo resultante debido a la torsión en cada pata del estribo es constante. Entonces:
\[{{\sigma }_{sw,T}}=\frac{{{F}_{sw,T}}}{{{a}_{sw,T}}}\]
dondeasw,T es el área total de los estribos que resisten la torsión por unidad de longitud.
En el caso de que los estribos individuales tengan materiales diferentes, debe tenerse en cuenta la rigidez axial de las barras individuales.
\[{{F}_{sw,T}}={{F}_{s1,T}}+{{F}_{s2,T}}+{{F}_{s3,T}}+...+{{F}_{sn,T}}=\sum\limits_{i=1}^{{{n}_{T}}}{{{F}_{si,T}}}\]
\[{{\varepsilon }_{sw,T}}=\frac{{{F}_{sw,T}}}{\sum\limits_{i=1}^{{{n}_{T}}}{\left( {{a}_{si,T}}\cdot {{E}_{si,T}} \right)}}\]
nT. . . . número de tramos de armadura (grupos de armaduras) que resisten la torsión
Fsi,T. . fuerza en el i-ésimo grupo de armadura resultante de la torsión por unidad de longitud
asi,T. . área transversal de la armadura de cortante que resiste la torsión por unidad de longitud
Esi,T. . . Módulo de elasticidad de Young del i-ésimo grupo de armadura resistente a la torsión
εsw,T. . deformación de la armadura debida a la torsión
La tensión resultante en cada estribo debido a la torsión aplicada se calcula como
\[{{\sigma }_{sw,i,T}}={{\varepsilon }_{sw,T}}\cdot {{E}_{si,T}}]
Interacción V+T
El cálculo de las tensiones en los estribos debidas al cizallamiento y a la torsión es entonces una suma de las tensiones debidas a los componentes individuales de la carga.
\[{{sigma }_{sw,i}}={{sigma }_{sw,i,V}}+{{sigma }_{sw,i,T}}]
Fuerza resultante en la i-ésima armadura:
\{{F}_{sw,i}={a}_{sw,i}\cdot {{sigma }_{sw,i}}]
Interacción de cortante, torsión y flexión para la armadura longitudinal
Determinación de la fuerza en cada armadura longitudinal debida a la fuerza normal y al momento flector
La aplicación RCS se utiliza para calcular la respuesta de la sección transversal debida a la combinación de la fuerza normal y el momento flector para determinar la tensión y la deformación en cada una de las barras longitudinales y la armadura de pretensado.
Determinación del esfuerzo en la armadura longitudinal individual debido al esfuerzo cortante
El incremento de la fuerza de tracción en la armadura longitudinal ΔFtd debido a la fuerza cortante depende de la geometría del modelo de puntal y tirante.
\[\Delta {{F}_{td}}={{V}_{ed}}left( \cot \theta -\cot \alpha \right)\}]
ΔFtd. . . incremento de la fuerza de tracción en la armadura longitudinal debido a la fuerza cortante.
Ved. . . . valor de cálculo del esfuerzo cortante que actúa en la sección considerada
θ . . . . el ángulo entre el puntal de compresión de hormigón y el eje del elemento
α . . . . ángulo entre la armadura de cortante y el eje del elemento
Para la armadura longitudinal situada en el cordón de tracción, la fuerza resultante Ft en la armadura longitudinal debida a la combinación N+M+V debe tomarse no mayor queMEd,max/z(dondeMEd,max es el momento máximo a lo largo de la viga)
\[{{F}_{t}=\frac{{M}_{Ed}}{z}+0,5{{V}_{ed}}left( \cot \theta -\cot \alpha \right)\le \frac{{{M}_Ed,\max }}{z}}].
La fuerza ΔFtd es transmitida por todos los tendones de pretensado adheridos y las armaduras situadas en la parte de la sección transversal que resiste el cortante (el alma en el caso de un perfil en I). Por seguridad, la contribución de la armadura de pretensado puede considerarse 0. La hipótesis del cálculo es que el incremento de la deformación axial de la armadura longitudinal individual que resiste el cortante es constante (Δεs1,V = Δεs2,V = .... =Δεp1,V = Δεp2,V = ... = ΔεV = const.). La derivación es válida para un diagrama de trabajo de armadura bilineal con una rama plástica horizontal. En el caso de un diagrama con una rama inclinada, el cálculo debe modificarse.
\[\Delta {{F}_{td}}=\Delta {{F}_{s}}+\Delta {{F}_{s}}]
\[\Delta {{F}_{td}=\Delta {{varepsilon }_{V}}\cdot \sum\limits_{i=1}^{{{n}{s,V}}{{A}_{sl,i,V}}\cdot {{E}{sl,i,V}}+Delta {{varepsilon }_{V}}\cdot {{suma_limits_i=1}^{{n}}{p,V}}{{A}{pl,i,V}}\cdot {{E}{pl,i,V}}]
ΔεV. . . . incremento de deformación en la armadura longitudinal debido al esfuerzo cortante.
ns,V. . . . número de armaduras longitudinales que resisten el esfuerzo cortante
Asl,i,V. . . área de la i-ésima armadura longitudinal que resiste el esfuerzo cortante
Esl,i,V. . . Módulo de elasticidad de Young de la i-ésima armadura longitudinal que resiste el esfuerzo cortante
np,V. . . . número de tendones que resisten el esfuerzo cortante
Apl,i,V. . . área del tendón i-ésimo que resiste el esfuerzo cortante
Epl,i,V. . . Módulo de elasticidad de Young del tendón i-ésimo que resiste la fuerza cortante
Una vez determinado el valor de la fuerza ΔFtd, puede calcularse la deformación media de la armadura ΔεV.
\[\Delta {{\varepsilon }_{V}}=\frac{\Delta {{F}_{td}}}{\sum\limits_{i=1}^{{{n}_{s,V}}}{{{A}_{sl,i,V}}\cdot {{E}_{sl,i,V}}}+\sum\limits_{i=1}^{{{n}_{p,V}}}{{{A}_{pl,i,V}}\cdot {{E}_{pl,i,V}}}}\]
Incremento de tensión en las barras longitudinales individuales debido al esfuerzo cortante aplicado:
para la barra corrugada \[\Delta {{sigma }_{sl,i,V}}=\Delta {{varepsilon }_{V}}\cdot {{E}_{sl,i,V}}].
para tendón \[\Delta {{sigma }_pl,i,V}}=\Delta {{varepsilon }_{V}}\cdot {{E}_{pl,i,V}}]
Determinación de la fuerza en cada armadura longitudinal por torsión
Es muy importante determinar las armaduras longitudinales que resisten la torsión. Estas son las armaduras que se encuentran en una sección transversal de pared delgada eficaz alternativa resistente a la torsión.
\[\frac{\sum{{{A}_{sl}}{{f}_{yd}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta \]
Según la norma EN 1992-1-1, deben cumplirse varias condiciones para el refuerzo resistente a la torsión longitudinal:
- la armadura debe distribuirse uniformemente a lo largo de la longitud zi, pero en secciones transversales pequeñas la armadura puede concentrarse en las esquinas del estribo
- la distancia axial máxima de la armadura longitudinal es de 350 mm
La contribución de la armadura de pretensado no se considera según la norma EN 1992-1-1.
El código EN 1992-2 establece que se puede considerar la contribución de la armadura de pretensado, pero el incremento máximo de tensión en la armadura de pretensado no superará Δσp ≤ 500MPa. Entonces se puede modificar la fórmula:
\[\frac{\sum{{{A}_{sl}}{{f}_{yd}}+\sum{{{A}_{p}}\Delta {{\sigma }_{p}}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta\]
Sin embargo, dado que se puede considerar el incremento del refuerzo de pretensado, pero queda a elección del usuario. Actualmente, la armadura de pretensado no se tiene en cuenta en el cálculo.
La hipótesis del cálculo es que el incremento de la deformación axial de cada armadura longitudinal resistente a cortante es constante (Δεs1,T = Δεs2,T = .... =Δεp1,T = Δεp2,T = ... = ΔεT = const.). La derivación es válida para un diagrama de trabajo de armadura bilineal con una rama plástica horizontal. En el caso de un diagrama con una rama creciente, el cálculo debe modificarse.
\[\frac{\sum\limits_{i=1}^{{{n}_{T}}}{{{A}_{sl,i,T}}\cdot \Delta {{\sigma }_{s,i,T}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta\]
\[\frac{\sum\limits_{i=1}^{{{n}_{T}}}{{{A}_{sl,i,T}}\cdot \Delta {{\varepsilon }_{T}}\cdot {{E}_{s,i,T}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta\]
|Delta {{varepsilon }_{T}}={frac{{T}_{ed}}{cdot {{u}{k}}{2{A}_{k}}{cdot \sum\limits_{i=1}^{{{n}{T}}{{A}{sl,i,T}}cdot {{E}{s,i,T}}}}}}\cot \theta]
\[\frac{\sum\limits_{i=1}^{{{n}_{T}}}{{{A}_{sl,i,T}}\cdot \Delta {{\sigma }_{s,i,T}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta\]
\[\frac{\sum\limits_{i=1}^{{{n}_{T}}}{{{A}_{sl,i,T}}\cdot \Delta {{\varepsilon }_{T}}\cdot {{E}_{s,i,T}}}}{{{u}_{k}}}=\frac{{{T}_{ed}}}{2{{A}_{k}}}\cot \theta\]
|Delta {{varepsilon }_{T}}={frac{{T}_{ed}}{cdot {{u}{k}}{2{A}_{k}}{cdot \sum\limits_{i=1}^{{{n}{T}}{{A}{sl,i,T}}cdot {{E}{s,i,T}}}}}}\cot \theta]
Ted. . . el valor de cálculo del par aplicado en la sección considerada
θ . . . . inclinación de las diagonales de compresión con respecto al eje longitudinal de la viga (idéntica a la del esfuerzo cortante)
uk . . . . perímetro del áreaAk
Af. . . superficie definida por el eje de la sección hueca de pared delgada de sustitución
ns,T. . . .número de armaduras longitudinales de hormigón que resisten el par de torsión
Asl,i,T. . superficie de la i-ésima armadura longitudinal de hormigón que resiste el momento de torsión
ΔεT. . . el cambio en la transformación de la armadura longitudinal debido al momento de torsión
Δσs,i,T. . cambio de la tensión en la i-ésima armadura longitudinal debido al momento de torsión
Esl,i,T. . módulo de elasticidad de la i-ésima armadura longitudinal de hormigón que resiste el momento de torsión
Incremento de tensión en cada armadura longitudinal debido al par aplicado:
\[\Delta {{sigma }_{sl,i,T}}=\Delta {{varepsilon }_{T}}\cdot {{E}_{sl,i,T}}].