Grietas

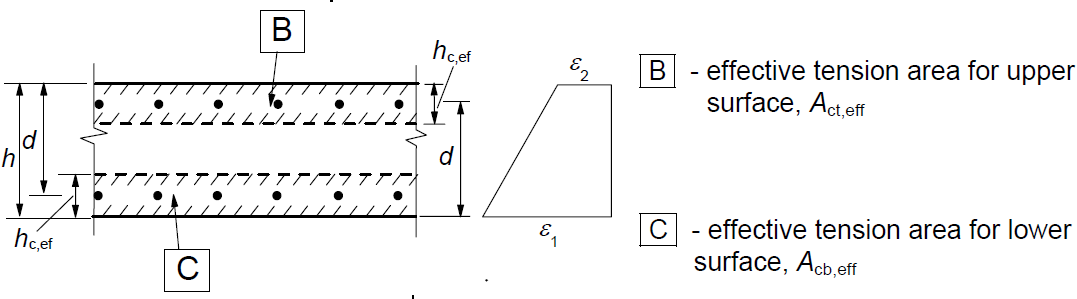
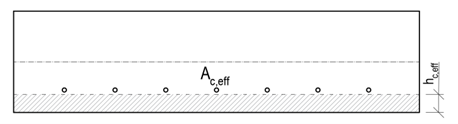
La formación de grietas

Un rasgo característico de las estructuras de hormigón armado sometidas a esfuerzos de flexión o tracción es la aparición de grietas en los puntos en los que el esfuerzo de tracción en el hormigón supera la resistencia a la tracción del hormigón. Para la durabilidad de la estructura y también para su estética, es importante garantizar que las grietas resultantes sean lo más pequeñas posible. El cálculo de la anchura de las fisuras, así como la anchura máxima permitida para las diferentes clases de exposición, se indican en la norma EN 1992-1-1, capítulo 7.3.

En el primer paso del cálculo, se determina si la sección transversal está agrietada o no. La propia anchura de la fisura se calcula siempre a partir de la combinación de carga cuasipermanente o frecuente (en función del anexo nacional), pero la formación de la fisura debe comprobarse a partir de todas las combinaciones de SLS especificadas. Por tanto, pueden darse dos casos:

• La tensión de tracción máxima en las fibras de hormigón no superará la resistencia a la tracción del hormigón a partir de ninguna combinación de carga (cuasipermanente_ME,qp, frecuente_ME,fr, o característica_ME,k), y por lo tanto consideramos la sección transversal sin fisuras.

\[{{M}_{E,i}}\le {{M}_{cr}}={{f}_{ct,ef}}\frac{{I}_{I}}{h-{{a}_{I}}}\]

• Si se desarrollan fisuras para cualquiera de las combinaciones (cuasipermanentes, frecuentes o características), es decir, el momento flector desarrollado a partir de la combinación de carga considerada es mayor que el momento crítico_Mcr, la sección transversal está fisurada a partir de esa combinación de carga, y deben calcularse las características de la sección transversal fisurada y la anchura de la fisura.

\[{{M}_{E,i}}>{{M}_{cr}}={{f}_{ct,ef}}\frac{{I}_{I}}{h-{{a}_{I}}}\]

_ME,i. . el momento flector obtenido a partir de algún peine de carga SLS. Por tanto, puede ser_ME,qp,_ME,fr o_ME,k.

fct_,ef . . la resistencia a tracción del hormigón en el momento considerado. Si el hormigón tiene más de 28 días, se considera una resistencia igual a _fctm.

Cálculo de la anchura de la fisura

En un elemento sometido a flexión, la formación de grietas se divide en 2 fenómenos:

• Fase de formación de la grieta (etapa número 2 en la Fig. 1)
• Desarrollo estabilizado de la grieta (etapa número 3 en la Fig. 1)

\[ \textsf{\textit{\footnotesize{Fig. 1 Etapas del comportamiento de la sección transversal de hormigón armado durante la carga}}]

Etapa de desarrollo de la grieta

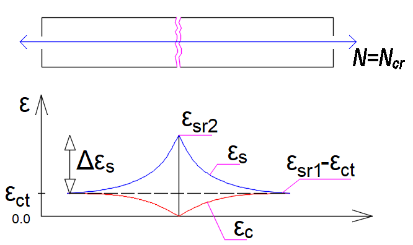
Se trata de la parte inicial del proceso, en la que las grietas individuales siguen apareciendo gradualmente hasta que toda la parte sometida a tracción del elemento se ve afectada por grietas que se distribuyen aproximadamente por igual a lo largo de la longitud del elemento. La primera grieta se forma cuando la fuerza en la banda sometida a tracción supera el valor de la fuerza crítica _Nr (fuerza de tracción crítica, véase más adelante), y se desarrollan más grietas hasta un nivel de carga que ejerce una fuerza en la banda sometida a tracción igual a 1,_3Ncr aproximadamente (fase número 2 en la Fig. 1).

\[ \textsf{\textit{\footnotesize{Fig. 2 Deformaciones del hormigón y la armadura en el momento de la primera fisura}}]

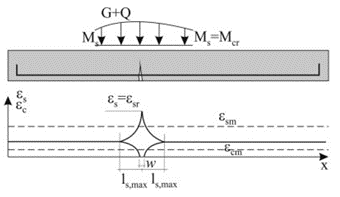
Las grietas en desarrollo se dividen en 2 tipos - grietas primarias y secundarias. Las grietas primarias se producen en las fibras de tracción cuando se alcanza la resistencia efectiva a tracción del hormigón (fct_,eff). Las grietas primarias representan el primer patrón de grietas (Fig. 2). A continuación, se forman grietas secundarias más cortas entre las grietas primarias (Fig. 3). A tensiones correspondientes a aproximadamente 1,2 a 1,5 _σsr (normalmente se considera un valor medio de 1,3 _σsr, donde _σsr es la tensión en la armadura en el momento de la formación de las fisuras primarias en la zona de tracción del hormigón), se completa también el desarrollo de las fisuras secundarias.

\[ \textsf{\textit{\footnotesize{Fig. 3 Fisuras primarias y secundarias}}]

La anchura de la grieta en la etapa de formación de grietas se puede calcular de la siguiente manera:

\[{{w}_{k}}=2{{l}_{s,\max }}left( {{\\varepsilon }_{sm}}-{\varepsilon }_{cm}} \right)\}]

\[ \textsf{\textit{footnotesize{Fig. 4 Características de la longitud de transmisión para la primera grieta}}]

Etapa de fisuración estabilizada

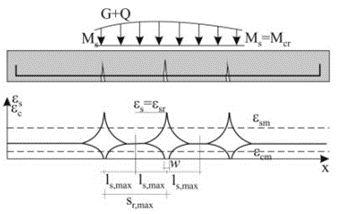
Después de superar aproximadamente 1,3 veces la fuerza crítica en la zona de tracción, no se forman nuevas grietas, el número de grietas en el elemento se estabiliza, y sólo la anchura de las grietas existentes aumenta con la carga adicional (etapa número 3 en la Fig. 1).

\[ \textsf{\textit{\footnotesize{Fig. 5 Deformaciones del hormigón y la armadura en la etapa de fisuración estabilizada}}]

La anchura de la grieta durante el desarrollo estable se puede calcular como:

\[{{w}_{k}={s}_{r,\max }}left( {{{varepsilon }_{sm}}-{{varepsilon }_{cm}} \right)\}]

\[ \textsf{\textit{footnotesize{Fig. 6 Agrietamiento estabilizado}}]

Fuerza de tracción crítica

El cálculo se basa en el Modelo de Cuerda de Tensión (TCM). La consideración básica es calcular la capacidad última de una banda de hormigón armado formada por una barra de refuerzo de área_As,eff rodeada por un área efectiva de hormigón de tracción_Ac,eff, que es capaz de resistir el esfuerzo de tracción hasta que se supera la resistencia a tracción fct_,eff (normalmente consideramos _fctm). Suponiendo una unión perfecta entre la armadura y el hormigón, podemos considerar que hasta que se produce la primera fisura, la remodelación de la armadura y del hormigón circundante es idéntica. Entonces se puede determinar la fuerza máxima en la banda de tracción justo antes de la primera fisura _Nr:

\[{{N}_{r}={A}_{c,eff}}\cdot {{f}_{ctm}}+{{A}_{s,eff}}\cdot {{sigma }_{s}}].

Introduciendo la sustitución

\[{{\alpha }_{e}}={}^{{{E}_{s}}}/{}_{{{E}_{cm}}};{{\rho }_{p,eff}}={}^{{{A}_{s,eff}}}/{}_{{{A}_{c,eff}}}\]

obtenemos:

\{{N}_{r}={A}_{c,eff}}\cdot {{f}_{ctm}}\cdot \left( 1+{{\alpha }_{e}}\cdot {{rho }_p,eff}} \right)\]

Justo después de la formación de la primera grieta, toda la fuerza _Nr es transferida por la armadura y por lo tanto la tensión en la armadura que pasa a través de la grieta recién formada se puede calcular como:

\{{{sigma }_{sr}}= {{frac{{f}_{ctm}}{{\rho }_{p,eff}} {{left( 1+{\alpha }_{e}} {{cdot {{\rho }_{p,Flecha derecha {{varepsilon}} = frac {{f}_{ctm}} {{E}{s} {\cdot {\rho }{p,eff}} {\left( 1+{alpha }_e} {\cdot {\rho }{p,eff}} {\right)\cdot]

Cálculo de la anchura de la grieta según CE 1992-1-1

La siguiente ecuación se utiliza para calcular la anchura de las fisuras en elementos de hormigón armado:

\[{{w}_{k}}={{s}_{r,\max }}left( {{\varepsilon }_{sm}}-{{\varepsilon }_{cm}} \right)\}]

_sr,max. . . separación máxima entre grietas

_εsm . . . la deformación media de la armadura a partir de la combinación de cargas, incluidos los efectos de la rigidización por tracción.

_εcm . . . deformación media del hormigón entre las fisuras

Cálculo de la diferencia de deformación

La diferencia de deformación de la armadura y del hormigón entre fisuras puede obtenerse a partir de la ecuación:

\[{{{varepsilon }_{sm}}-{{{varepsilon }_{cm}}=\frac{{{\sigma }_{s}}-{{k}_{t}}\cdot \frac{{{f}_{ct,eff}}}{{{{rho }_{p,eff}}}\cdot \left( 1+{{\alpha }_{e}}\cdot {{\rho }_{p,eff}} \right)\,}{{{E}_{s}}}\ge 0,6\frac{{{\sigma }_{s}}}{{{E}_{s}}}\]

σs_. . . . la tensión en la armadura en la fisura a partir de la combinación de cargas considerada

_{kt .} . . coeficiente empírico que tiene en cuenta la deformación media, en función de la duración de la carga. Puede tomar valores de 0,6 para el análisis a corto plazo. Para el análisis a largo plazo, se tiene en cuenta la reducción de la rigidez del material compuesto hasta aproximadamente el 70%, por lo que su valor es 0,4, que incluye la tasa de degradación de la cohesión entre la armadura y el hormigón debida al tiempo.

_αe. . . la relación efectiva de los módulos elásticos

\[{{\alpha }_{e}}={}^{{{E}_{s}}}/{}_{{{E}_{cm}}}\]

_ςp,eff. . . . . nivel efectivo de refuerzo

\izquierda( {{A}_{s,eff}}+{{xi }^2}_{1}A_{p}^{acute}} {derecha)}/{{A}_{c,eff}}]

_Ac, eff . . . . área efectiva del hormigón en tensión alrededor de la armadura (determinación de_Ac, eff más adelante)

_As,eff. . . . el área de la armadura adherida situada en el área de_Ac,eff

_Ap' . . . es el área de los tendones pretensados o postensados dentro de_Ac,eff

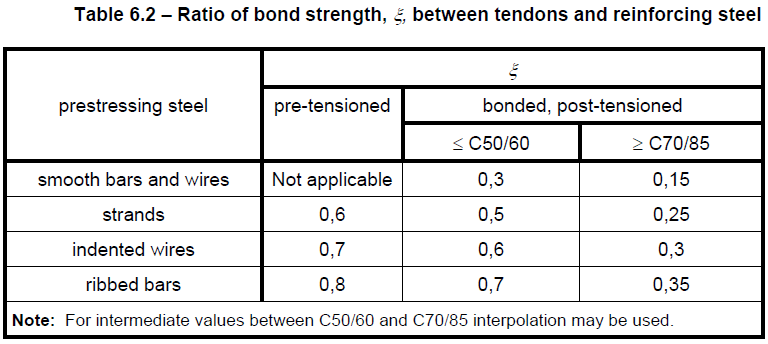
_ξ1. . . . es la relación ajustada de la resistencia de adherencia, teniendo en cuenta los diferentes diámetros del acero de pretensado y de armadura:

\[{{\xi }_{1}}=\sqrt{\xi \,\cdot \,\frac{{{\phi }_{s}}}{{{\phi }_{p}}}}\]

ξ . . . la relación entre la resistencia de adherencia del acero de pretensado y del acero de armadura (tabla 6.2)

_ϕs. . diámetro mayor de la barra de acero de refuerzo

_ϕp. . diámetro o diámetro equivalente del acero de pretensado

Para los haces,_Ap es el área de la armadura en el tendón

\[{{\phi }_{p}}=1,6\sqrt{{{A}_{p}}}\]

Para torones simples de siete alambres, donde _φwire es el diámetro del alambre

\[{{\phi }_{p}}=1,75\,\,{{\phi }_{hilo}}]

Para cordones simples de tres hilos en los que _φwire es el diámetro del hilo

\[{{\phi }_{p}}=1,20,\,{{\phi }__{hilos}}]

Si sólo se utiliza armadura de pretensado para evitar la fisuración, hay que tener en cuenta lo siguiente.

\[{{\xi }_{1}}=\sqrt{\xi \,}\]

En elementos pretensados, no se requiere un área mínima de armadura adherida siempre que, bajo la combinación característica de carga y el valor característico de la fuerza de pretensado, el esfuerzo de tracción en cualquier fibra no sea mayor que la resistencia a tracción del hormigón, fct_,eff. (véase EN 1992-1-1 cap. 7.3.2 para más detalles)

El área efectiva del hormigón en tensión

Un paso importante pero a la vez el más complicado del cálculo es determinar el área efectiva del hormigón en tracción que rodea la armadura. Tanto el Eurocódigo como el Código Modelo consideran modos de carga simples, en los que el elemento de hormigón armado se carga por flexión o tracción uniaxial. El valor de la altura efectiva se determina como:

\[{{h}_{c,eff}}=\min \left\{ 2,5\left( h-d \right);\frac{\left( h-x \right)}{3};{}^{h}/{}_{2}} {\i1}{\i}{\i} {\i}{\i} {\i}{\i}

\[ \textsf{\textit{footnotesize{Fig. 6 Determinación de Ac,eff para barras flexionadas (izquierda) y barras en tensión (derecha)}}]

Normalmente, el valor hc_,eff = 2,5(h-d) es crítico. Para elementos tensados, el límite superior es h/2, mientras que para elementos flexionados es (h-x)/3. Sin embargo, el área_Ac,eff también está limitada por la anchura determinada a partir de la ecuación 5(c+ϕ/2). Si la separación de las armaduras es superior a 5(c+ϕ/2), entonces se considera el área efectiva del hormigón tensado de anchura 5(c+ϕ/2) para las barras individuales.

\[ \textsf{\textit{\footnotesize{Fig. 9 Determinación de Ac,eff en función de la separación entre armaduras}}]

Distancia máxima de fisura

Al calcular la distancia máxima de fisuración_sr,max, pueden darse dos casos:

• La distancia axial de las armaduras adheridas no supera una distancia de 5(c+ϕ/2) - Fig. 9a
• La distancia axial de las armaduras adheridas es superior a 5(c+ϕ/2) - Fig. 9b

El cálculo de la distancia máxima de fisuración_sr,max para el caso de que las distancias axiales de las armaduras no superen el valor 5(c+ϕ/2 ) se define como sigue:

\[{{s}_{r,\max }}={{k}_{3}c+{{k}_{1}}{{k}_2}}{{k}_{4}}frac{{\phi }{{\rho }_{p,eff}}].

c _. . . . valor de recubrimiento concreto en mm. Dado que el valor del recubrimiento puede ser diferente para la armadura de borde tanto horizontal como vertical, se recomienda considerar el valor máximo de recubrimiento encontrado para la armadura considerada.

_ϕ . . . . diámetro de la armadura adherida. En el caso de diámetros de armadura diferentes, el diámetro equivalente se calculará de acuerdo con la ecuación 7.12 de la norma EN 1992-1-1.

\[{{\phi }_{eq}}={\frac{{{n}_{1}\phi _{1}^{2}+{{n}_{2}\phi _{2}^{2}}{{{n}_{{phi }_{1}+{{n}_{2}}{{\phi }_{2}}].

_k1. . . . es un coeficiente que tiene en cuenta las propiedades de adherencia de la armadura adherida

• _k1 = 0,8 para barras de alta adherencia
• _k1 = 1,6 para barras con una superficie efectivamente lisa (por ejemplo, tendones de pretensado)

_k2. . . . es un coeficiente que tiene en cuenta la distribución de la deformación

• _k2 = 1,0 para flexión
• _k2 = 0,5 para tracción pura

Para los casos de tensión excéntrica o para zonas locales, deben utilizarse valores intermedios de _k2 que pueden calcularse a partir de la relación:

\[{{k}_{2}}=\frac{{\\varepsilon }_{1}}+{{\varepsilon }_2}}{2{\varepsilon }_{1}}].

k3_. . . coeficiente que expresa la longitud de la zona próxima a una fisura en la que se rompe la unión entre el hormigón y la armadura. El valor recomendado del CE básico _k3 = 3,4 puede ser modificado por el Anexo Nacional.

El coeficiente k4_. . . expresa la relación entre la adherencia y la resistencia a tracción del hormigón. El valor recomendado del CE básico k4 = 0,425 puede ser modificado por el Anexo Nacional.

El cálculo de la distancia máxima de fisuración_sr,max para el caso de que las distancias axiales de las armaduras superen el valor 5(c+ϕ/2) se define como sigue:

\[{{s}_{r,\max }}=1,3\left( h-x \right)\]

Valores máximos de distancia de fisura según la ecuación

\[{{s}_{r,\max }}=1,3\left( h-x \right)\]

deben ser siempre superiores a los valores determinados por la ecuación

\{{s}_{r,\max }}={k}_{3}c+{{k}_{1}{k}_2}}{k}_{4}{{phi }/{{rho }_p,eff}};\}].

de lo contrario, se recomienda considerar la distancia mayor obtenida a partir de las ecuaciones anteriores. La ecuación de la deformación en el hormigón/refuerzo no se modifica para el caso de la distancia axial grande del refuerzo. En zonas con anchuras de fisura controladas, la distancia axial de las armaduras individuales no debe ser superior a 5(c+ϕ/2).

Cálculo de la anchura de fisura implementado en RCS

Determinación del área efectiva_Ac,eff

Dado que no es tan sencillo determinar qué armadura puede considerarse como armadura longitudinal resistente a la fisuración,_Ac, eff se determina mediante el siguiente proceso iterativo.

• De todas las armaduras que actúan a tracción, se determina el centro de la fuerza de tracción Cg_,s,1. La profundidad efectiva de la armadura d es la distancia entre Cg_,s, y la fibra de hormigón más comprimida calculada en la dirección del momento flector resultante. Al mismo tiempo, se determinan la posición del eje neutro y la altura de la zona comprimida x para la sección fisurada. Esto permite determinar la altura efectiva hc_,eff:

\[{{h}_{c,eff}}=\min \left\{ 2,5\left( h-d \right);\frac{\left( h-x \right)}{3};{}^{h}/{}_{2}} {\a6}[\a6}[\a6}[\a6}[\a6]

• Excluyendo todas las armaduras que se encuentran fuera de_Ac,eff,1, se determina el nuevo centro de la armadura Cg_,s,2, junto con la nueva profundidad efectiva de la armadura d, la altura efectiva hc_, eff se determina de la misma manera que en el paso anterior, sólo que con los valores de entrada cambiados.

De nuevo, se comprueba que toda la armadura tensada considerada se encuentra en la_Ac,eff,2. Si esta condición se cumple, la iteración puede ser terminada y los valores de hc_,eff,2,_Ac,eff,2 y_As,eff,2 se muestran como los valores resultantes en IDEA StatiCa RCS.

Posibles casos de cálculo del ancho de fisura

En general, pueden darse tres casos en el cálculo del ancho de fisura:

• La armadura de tracción se encuentra en la región_Ac,eff, siendo la distancia axial de las armaduras individuales inferior a 5(c+ϕ/2). Entonces se utilizan las siguientes definiciones para el cálculo:

\[{{s}_{r,\max }}={{k}{3}c+{{k}_{1}}{{k}_2}}{{k}_{4}}frac{{\phi }{{\rho }_{p,eff}}].

\{ {{varepsilon }_{sm}}-{{\\varepsilon }_{cm}}={frac{{\sigma }_{s}}-{{k}_{t}},{\cdot,{frac{{{f}_{ct,eff}}}-{{\rho }_{p,eff}},\0,6frac {{sigma}} {{E}{s}}}]

• El refuerzo de tracción se encuentra en el_Ac,eff, con la distancia axial de los refuerzos individuales superior a la distancia 5(c+ϕ/2). A continuación, se utilizan las siguientes definiciones para el cálculo:

\[{{s}_{r,\max }}=1,3\left( h-x \right)\]

\[{{{varepsilon }_{sm}}-{{{varepsilon }_{cm}}={frac{{{sigma }_{s}}-{k}_{t}},\cdot \,\frac{{{f}_{ct,eff}}}{{{\rho }_{p,eff}},\0,6frac {{sigma}} {{E}{s}}}]

• La armadura de tracción no se encuentra en el_Ac,eff (esto puede deberse, por ejemplo, a una cubierta gruesa).

En este caso no sería posible calcular la anchura de las grietas. Por lo tanto, el cálculo de la altura efectiva hc_,eff se modifica como sigue:

\[{{h}_{c,eff}}=\min \left\{ 2,5\left( h-d \right);h/2 \right\}].

Al mismo tiempo, aparece la siguiente disconformidad:

El área efectiva de hormigón en tensión que rodea a la armadura o tendones de pretensado de profundidad hc_,eff, donde hc_, eff es el menor de 2,5(h - d) o h/2. Considerando el valor como(h - x)/3, la armadura está fuera del área efectiva de hormigón en tensión, y por lo tanto no sería posible calcular el ancho de fisura de acuerdo con la cláusula 7.3.4.