La entrada de fuerzas internas
La entrada de los esfuerzos internos de los elementos 2D depende del tipo de elemento 2D:
- Casco-losa - se pueden introducir los esfuerzos de membrana (nx, ny y nxy), momentos flectores (mx,my y mxy) y esfuerzos cortantes (vx y vy)
- Forjado-muro - se pueden introducir los esfuerzos de membrana (nx, ny y nxy), los momentos flectores (mx,my y mxy) y los esfuerzos cortantes (vx y vy).
- Losa: sólo se pueden introducir los momentos flectores (mx,my y mxy) y los esfuerzos cortantes (vx y vy).
- Muro - sólo se pueden introducir los esfuerzos de membrana (nx, ny y nxy)
- Viga profunda - sólo se pueden introducir los esfuerzos de membrana (nx, ny y nxy)
| Descripción | |
| mx(y) | Momento flector en la dirección del eje x (y). Un valor positivo provoca tensión en la superficie inferior de un elemento 2D. |
| mxy(yx) | Momento de torsión en torno al eje y (x)-que actúa sobre la arista paralela al eje x (y). Un valor positivo provoca un esfuerzo cortante tensional en la superficie inferior de un elemento 2D. Debido a que en cada punto del teorema del elemento 2D la igualdad de los esfuerzos cortantes horizontales es válida, los momentos torsores mxy =myx son iguales en cada punto del elemento 2D también. Por lo tanto, sólo el valor de mxy se introduce en el programa. |
| nx(y) | Fuerza normal en la dirección del eje x(y). El valor positivo actúa en la dirección del eje x(y) y causa tensión en la sección. |
| nxy(yx) | Fuerza normal que actúa en el plano central en la dirección del eje y(x) sobre la arista paralela al eje x(y). El valor positivo actúa en la dirección del eje x(y). Debido a que en cada punto del elemento 2D el teorema de la igualdad de los esfuerzos cortantes horizontales es válido, las fuerzas normales nxy = nyx son iguales en cada punto del elemento 2D también. Por lo tanto, sólo el valor de nxy se introduce en el programa. |
| vx(y) | Fuerza cortante que actúa perpendicular al plano central en la arista paralela al eje x(y). El valor positivo actúa en la dirección del eje z. |
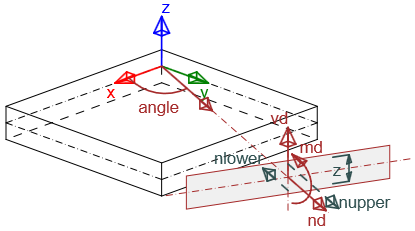
\[ \textsf{\textit{footnotesize{Convención de signos de fuerzas internas}}]
Para las comprobaciones deben definirse los siguientes tipos de combinaciones:
- Estado límite último/Accidental - los componentes de fuerza interna definidos para este tipo de combinaciones se utilizan para las comprobaciones ULS de elementos 2D:
- Capacidad N-M-M
- Respuesta N-M-M
- Interacción
y la comprobación de las disposiciones de detalle
- Característica - los componentes de fuerza interna definidos para este tipo de combinación se utilizan para la comprobación de la limitación de tensiones (SLS)
- Cuasipermanente : los componentes de la fuerza interna definidos para este tipo de combinación se utilizan para comprobar la anchura de la fisura (SLS).
| Observación: |
| No es necesario introducir los componentes de las fuerzas internas vx y vy para los tipos de combinación Característica y Cuasi-permanente, porque estos valores no se utilizan en las comprobaciones. |
Determinación de la dirección de la comprobación
La dirección de la comprobación debe determinarse para la correcta comprobación del elemento 2D. La dirección de la comprobación puede introducirse para cada tipo de combinación por separado, utilizando los dos métodos siguientes:
- Dirección definida por el usuario : el usuario define la dirección de comprobación como un ángulo relativo al eje x en el plano del elemento 2D. Esta opción se establece por defecto para el tipo de combinación ULS y el valor predefinido del ángulo es 0 grados. Las comprobaciones se realizan en las siguientes direcciones:
- Dirección definida
- Dirección perpendicular a la dirección definida
- Dirección de la diagonal de compresión en la superficie superior
- Dirección de la diagonal de compresión en la superficie inferior
- Dirección de lastensiones principales - la dirección de comprobación se calcula automáticamente como la dirección de las tensiones principales en la superficie superior e inferior del elemento 2D. Esta opción se establece por defecto para los tipos de combinación Característica y Cuasi-permanente. Las comprobaciones se realizan en las siguientes direcciones:
- Dirección de las tensiones principales en la superficie inferior
- Dirección perpendicular a la dirección de las tensiones principales en la superficie inferior
- Dirección de la diagonal de compresión en la superficie inferior
- Dirección de las tensiones principales en la superficie superior
- Dirección perpendicular a la dirección de las tensiones principales en la superficie superior
- Dirección de la diagonal de compresión en la superficie superior
\[ \textsf{\textit{\footnotesize{Esfuerzos internos calculados en la dirección de entrada según la teoría de Baumann}}]
Análisis de la dirección de comprobación para el estado límite último
Análisis 1
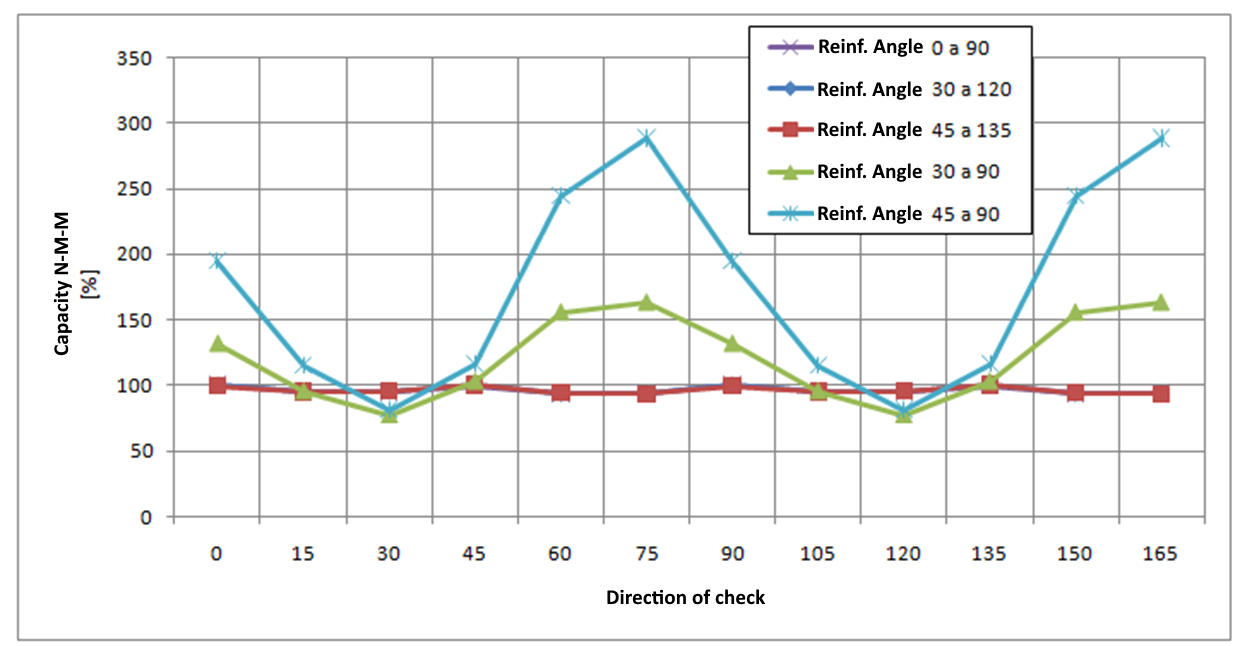
Para un elemento 2D cargado sólo por momentos flectores (mx = 20 kNm/m,my = 10 kNm/m, mxy = 5 kNm/m ) con el ángulo de la armadura y el ángulo de la dirección de comprobación cambiados para el estado límite último - los resultados se muestran en el siguiente gráfico:
El análisis implica:
- Si las barras de refuerzo son perpendiculares entre sí, los resultados de la comprobación son similares para diferentes ángulos de dirección de comprobación, no dependen del ángulo de refuerzo definido y el valor máximo de la comprobación se encuentra para los ángulos 0, 45 y 90 grados. Por lo tanto, esta comprobación puede realizarse para una dirección predefinida de un ángulo de comprobación de 0 grados.
- Si las barras de refuerzo no son perpendiculares entre sí, los resultados de las comprobaciones difieren significativamente y el valor máximo de comprobación se alcanza aproximadamente en la dirección correspondiente a la dirección del refuerzo medio. Por lo tanto, se recomienda cambiar la dirección de comprobación predefinida o realizar comprobaciones en más direcciones en los casos en que las barras de refuerzo no sean perpendiculares entre sí.
Análisis 2
Para la armadura ortogonal, se han cambiado los valores de los momentos flectores y el ángulo para la comprobación del código ULS. Los resultados se representan en el gráfico:
El análisis implica que incluso para diferentes valores de momentos flectores, el valor máximo de la comprobación del estado límite último se encuentra para las direcciones de comprobación 0, 45 y 90 grados. Por tanto, la comprobación puede realizarse para un ángulo de comprobación predefinido de 0 grados. Una conclusión similar es válida para elementos 2D cargados sólo por la fuerza normal o cargados por la fuerza normal combinada con momentos flectores.
Recálculo de esfuerzos internos en las direcciones de comprobación
Los esfuerzos internos definidos se recalculan a las direcciones de comprobación utilizando la fórmula de transformación de Baumann, descrita en Baumann, Th. : "Zur Frage der Netzbewehrung von Flächentragwerken". En : Der Bauingenieur 47 (1972), Berlín 1975. El procedimiento de cálculo es el siguiente
- Cálculo de las fuerzas normales en ambas superficies del elemento 2D
- Cálculo de los esfuerzos principales en ambas superficies del elemento 2D
- Cálculo de las fuerzas recalculadas para cada superficie en la dirección de comprobación definida
- Cálculo de esfuerzos recalculados para cada superficie hacia el centro
- Recálculo de esfuerzos cortantes en la dirección de comprobación definida
Cálculo de las fuerzas normales en ambas superficies del elemento 2D
Las fuerzas internas definidas se recalculan a ambas superficies utilizando las siguientes fórmulas:
\[{{n}_{x,low\left( upp \right)}}=\frac{{{n}{x}}{2}+\left( - \right)\frac{{{m}{x}}{z}].
\{{n}{y,low\left( upp \right)}}={frac{{{n}{y}}{2}+{left( - \right)\frac{{{m}{y}}{z}]
~~~~~ {{n}_{xy,low\left( upp \right)}}={frac{{{n}_{xy}}{2}+{left( - \right)\frac{{{m}{xy}}{z}]
El brazo de palanca de las fuerzas internas (z) debe determinarse para el recálculo de las fuerzas internas. El brazo de palanca de las fuerzas internas se determina a partir del método de la deformación límite en la carga por el momento principal de flexión en las direcciones de los momentos principales m1 en ambas superficies. Si los momentos principales son iguales a cero o si no se encuentra el equilibrio en la dirección de los momentos principales, el brazo de palanca de las fuerzas internas se determina según la fórmula:
\[z=x\cdot d\]
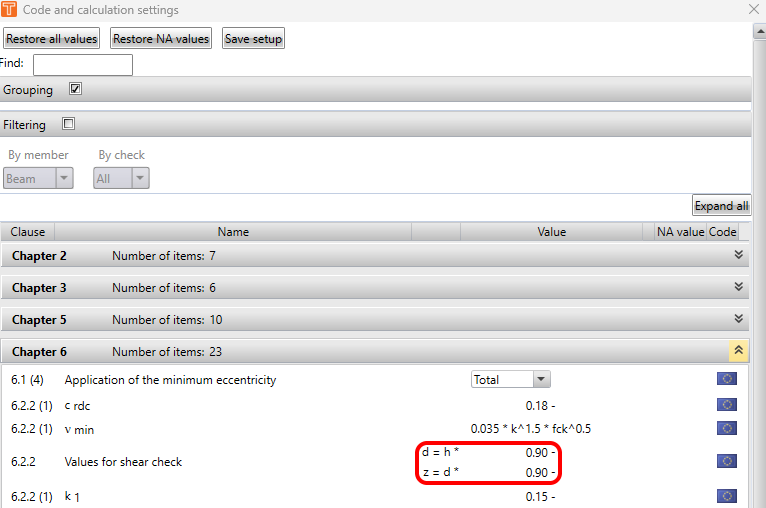
| Descripción | |
| x | El coeficiente para el cálculo del brazo de las fuerzas internas se define en la configuración del código nacional. |
| d | Altura efectiva de la sección transversal calculada por separado para las superficies superior e inferior del elemento 2D. Para la superficie inferior, es una distancia desde el centroide de las barras de refuerzo en la superficie inferior hasta el borde superior de la sección transversal. Para la superficie superior, es una distancia desde el centroide de las barras de refuerzo en la superficie superior hasta el borde inferior de la sección transversal. |
| Observación: |
| El brazo de los esfuerzos internos puede verificarse en la comprobación Respuesta N-M-M. Sólo deben introducirse los momentos flectores y la dirección de comprobación debe coincidir con la dirección del momento principal. |
En el siguiente diagrama, se muestra una verificación del brazo de palanca de los esfuerzos internos para momentos flectoresmx = 20 kNm/m,my = 10 kNm/m, mxy = 5 kNm/m. La dirección de los momentos principales se ha calculado como αm1 = 22,5 grados y la respuesta de la sección transversal se ha calculado para determinar el brazo de palanca de los esfuerzos internos.
| Observación: |
| Los brazos de palanca de las fuerzas internas para el recálculo de las fuerzas internas en la dirección de la comprobación y los brazos de palanca de las fuerzas internas para las comprobaciones pueden ser diferentes, ya que el brazo de palanca de las fuerzas internas para el recálculo se determina en una sección transversal cargada por momentos principales en la dirección de los momentos principales, y el brazo de palanca de las fuerzas internas para la comprobación se determina en una sección transversal cargada por momentos flectores y fuerzas normales en la dirección de la comprobación. Los valores de los brazos de palanca de los esfuerzos internos para todos los tipos de combinación se muestran en la tabla Esfuerzos recalculados en el navegador Esfuerzos internos en la sección. |
Cálculo de esfuerzos internos en ambas superficies
Los esfuerzos principales en ambas superficies del elemento 2D se calculan utilizando la fórmula:
\{{n}{1}{2}}={fracción}{{n}{x,baja izquierda( arriba \ derecha)+}{n}{y,baja izquierda( arriba \ derecha)}}{2}+{fracción{1}{2}}sqrt{{{{n}{ izquierda( arriba \ derecha)-}{n}{y,baja izquierda( arriba \ derecha)}} \}^{2}}+4\cdot {{n}_{xy,low\left( upp \right)}}]
\{{n}{2,bot}{2}{2}={frac}{{n}{x,bot}{2}{2}{2}}-{frac}{1}{2}{2}{sqrt}{{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{2}{4}{4}{cdot} {{n}{x,bot}{2}{2}{2}{2} \}^{2}}+4\cdot {{n}_{xy,low\left( upp \right)}}]
Y la dirección de las fuerzas principales se calcula mediante la fórmula:
\{{{alpha}}{{n1,baja izquierda( arriba a la derecha)}}=0,5 {{\cdot {{\tan}}^{-1}} {{frac{2{\cdot {{n}{xy,baja izquierda( arriba a la derecha)}}{{{n}{x,baja izquierda( arriba a la derecha)}}-{{n}{y,baja izquierda( arriba a la derecha)}}. \derecha)}]
| Observación: |
| Los esfuerzos principales y la dirección de los esfuerzos principales para ambas superficies del elemento 2D se muestran para todos los tipos de combinación en la tabla Esfuerzos recalculados en el navegador Esfuerzos internos en la sección. |
Cálculo de los esfuerzos internos recalculados en las superficies a la dirección de comprobación definida
El recálculo de los esfuerzos principales en las direcciones de comprobación se realiza por separado para cada superficie utilizando la fórmula de transformación de Baumann:
\[{{n}_{superficie,i,baja\izquierda( upp \derecha)}}=\frac{{{n}_{1,baja\izquierda( upp \derecha)}}\cdot \sin \izquierda( {{{alfa }_{j,baja\izquierda( upp \derecha)}} \...izquierda( {{alpha }_k,low\left( upp \right)}} + {{n}_{2,baja izquierda( arriba derecha)}} {\cdot \cos \left( {{alpha }_{j,baja izquierda( arriba derecha)}} \...derecha)\cdot \cos \left( {{alpha }_{k,low\left( upp \right)}} \...-sin izquierda( {{{alfa_j,baja izquierda( arriba derecha)}}-{{{alfa_i,baja izquierda( arriba derecha)}} \...derecha)\cdot \sin \izquierda( {{{alfa}{k,izq.baja( derecha)arriba)}}-{{{alfa}{i,izq.baja( derecha)arriba)}} derecha) \...derecha)}]
| Descripción | |
| i, j, k, i | Índice de la dirección de comprobación (dirección de recálculo de fuerzas internas) i, j, k, i = 1, 2, 3, 1 . E. G. Para superficie inferior y cálculo de fuerza en dirección j (ángulo α2) la fórmula es: \[{{n}_{superficie,2,baja}}=\frac{{{n}_{1,baja}}\cdot \sin{{alfa }_3,baja}}\cdot \sin{{alfa }_1,baja}}+{{n}_2,baja}}\cdot \cos{{alfa }_3izquierda( {{alpha }_3,low}}-{{\\alpha }_2,low}} derecha)\cdot \sin izquierda( {{{alpha }_1,low}}-{\\alpha }_2,low}} derecha)\cdot \cdot \sin izquierda( {{{\alpha }_1,low}}-{{\alpha }_2,low}} derecha) |
| \{{{alpha }_{i,j,k,low\left( upp \right)}}} | Ángulo entre la dirección de comprobación definida o la dirección del puntal de compresión y la dirección de los esfuerzos principales en la superficie inferior o superior del elemento 2D. Dirección de comprobación definida α1, low( upp) = α1 - α low(upp) Dir. perpendicular a la dirección definida α2, low(upp) = α2 - α low(upp) La dirección de comprobación del puntal de compresión α3, low(upp) = α3 - α low(upp) |
| α1 | Dirección de comprobación definida para la combinación concreta |
| α2 | La dirección perpendicular a la dirección definida, α2= α1 + 90 grados |
| α3 | Compruebe la dirección en la dirección del puntal de compresión en el plano del elemento 2D. Esta dirección se optimiza para minimizar la fuerza en esta dirección. |
| Observación: |
Si la dirección de comprobación es idéntica a la dirección de las Tensiones principales, las fuerzas en el puntal de compresión son nulas, por lo que esta dirección se desprecia en la comprobación La dirección del puntal de compresión para todos los estados de tensiones excepto el estado hiperbólico de tensiones (n1,low(upp) > 0 y n1,low(upp) < 0) puede calcularse según la fórmula: α3 = 0,5(α1 + α2) Las fuerzas internas recalculadas para ambas superficies del elemento 2D y todas las direcciones de comprobación incluyendo la dirección del puntal de compresión se muestran en la tabla Fuerzas recalculadas |
Transformación de los esfuerzos internos recalculados al centroide de la sección transversal
Para la comprobación del elemento 2D, los esfuerzos superficiales en una dirección particular deben ser recalculados al centroide de la sección. El resultado es la fuerza normal nd,i y el momento flector md,I actuando en el centroide de la sección transversal del elemento 2D.
md,i = nlower,i-zs,low + nupper,i-zs,upp
nd ,i = nlower,i + nupper,i
| Descripción | |
| nlower,i | Fuerzas de superficie recalculadas en la superficie inferior en la dirección de comprobación i-ésima, cuando nlower,i = nsurface,low,i. |
| nupper,i | Fuerzas internas recalculadas en la superficie superior en la dirección de comprobación i-ésima, cuando nupper,i = nsurface,upp,i. |
| zs,low (upp) | Distancia del centroide del hormigón comprimido o centroide de la armadura en la superficie inferior (superior), cuando z = zs,low + zs,upp |
| Observación: |
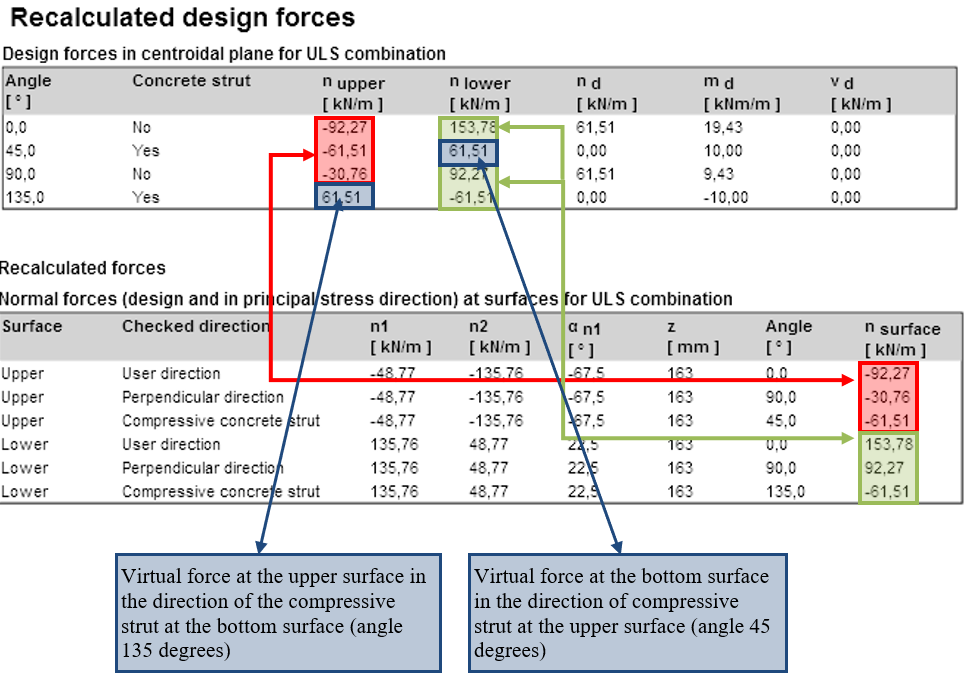
| Si las direcciones de los puntales de compresión en la superficie inferior y superior son diferentes, para el recálculo de fuerzas al centroide es necesario calcular fuerzas virtuales en la superficie inferior en la dirección del puntal de compresión en la superficie superior y viceversa. |
\[ \textsf{\textit{footnotesize{Fuerzas de diseño recalculadas}}]
Recálculo de esfuerzos cortantes en la dirección de comprobación definida
Los esfuerzos cortantes se recalculan en la dirección de la comprobación utilizando la fórmula:
\{{v}_{d,i}}={v}_{x}}\cdot \cos ({{alpha }_{i}})+{v}_{y}}\cdot \sin ({{alpha }_{i}})].
y la fuerza de corte máxima es
\[{{v}_{d,max~}}=\sqrt{{{v}_{x}}^{2}+{{v}_{y}}^{2}}\]
y actúa en la dirección
\[\beta ={\tan }^{-1}}\left( \frac{{v}_{y}}{{v}_{x}} right)\]
| Descripción | |
| αi | Comprueba el ángulo en la dirección i-ésima |
| Observación: |
| Cuando se comprueba un elemento 2D con esfuerzos cortantes relativamente grandes es conveniente comprobar el elemento 2D en la dirección del esfuerzo cortante máximo, lo que significa que la comprobación de la dirección definida corresponde al ángulo β |
Comparación del recálculo de esfuerzos internos utilizando varios métodos
Recálculo de esfuerzos según EN 1992-1-1
El método descrito en EN 1992-1-1 se utiliza en varios programas y en la práctica para calcular los esfuerzos internos de cálculo. EN 1992-1-1 sólo tiene en cuenta las direcciones perpendiculares de la armadura. El cálculo de las fuerzas de dimensionamiento con la influencia del momento torsor se describe en el siguiente diagrama de flujo, dondemy³mx. Se puede crear un diagrama similar para momentosmy <mx
| Descripción | |
| mxd+, mxd- | Momento flector acotado en la dirección del eje x para el diseño y comprobación de la armadura en la superficie inferior (-) o superior (+) |
myd+ myd- | Momento flector acotado en la dirección del eje y para el cálculo y comprobación de la armadura en la superficie inferior (-) o superior (+). |
| mcd+, mcd- | Momento flector de dimensionamiento en el puntal de hormigón a compresión en la superficie inferior (-) o superior (+), que debe soportar el hormigón |
Los valores de los esfuerzos de dimensionamiento recalculados para el tipo de elemento = Losa, calculados utilizando el método descrito en EN, se muestran en la siguiente tabla:
En IDEA StatiCa RCS los valores de los momentos en la superficie superior e inferior no se muestran, pero los valores de las fuerzas normales en ambas superficies y los valores de los momentos recalculados al centroide de la sección transversal.
Los momentos en las superficies inferior y superior se pueden calcular utilizando las fuerzas superficiales, que se muestran en la salida numérica, utilizando la fórmula:
\[{{m}_{superficie,i,dlow\left( upp \right)}}={{n}_{superficie,i,low\left( upp \right)}}\cdot z\].
Los valores de las fuerzas de superficie y los momentos recalculados se muestran en las siguientes tablas:
Las tablas muestran, que los momentos en las superficies de las losas calculados en IDEA Concrete y calculados de acuerdo con el método descrito en EN, se corresponden sólo en una superficie. Esta diferencia es causada por la diferente optimización del puntal de hormigón. El método utilizado en IDEA StatiCa RCS busca el ángulo del puntal de compresión en la fuerza mínima en el puntal. El método descrito en ES busca una suma mínima de fuerzas negativas de todas las direcciones.
Comparación del cálculo de esfuerzos internos con los programas RFEM y SCIA Engineer
Para comparar los resultados de los esfuerzos internos recalculados en los programas IDEA Concrete, RFEM y SCIA Engineer (SEN) se preparó un modelo simple de losa de dimensiones 6 m x 4 m y espesor 200 mm. La losa está apoyada con apoyos lineales en los bordes y cargada con una carga uniforme de 10 kN/m2.
Para simplificar la presentación, sólo se muestran los valores de los esfuerzos internos recalculados en una sección longitudinal. La distancia de la sección desde el borde de la losa es de 1,5 m. Los esfuerzos internos calculados en el programa RFEM se utilizaron como valores de entrada para IDEA Concrete.
La tabla muestra un buen cumplimiento de los esfuerzos calculados en programas particulares.