Doblar

Métodos de comprobación de la capacidad seccional

Para comprobar el estado límite último de elementos de hormigón 1D se pueden utilizar dos métodos bien conocidos. El primero nos dará la capacidad última de la sección transversal en forma de área de interacción o diagrama de interacción (en el caso de momento flector en una dirección).La capacidad de la sección transversal puede determinarse como la relación entre las fuerzas internas actuantes y las fuerzas del estado límite. La segunda consiste en encontrar el equilibrio en una sección transversal, donde buscamos el comportamiento real de la sección cargada, el uso de materiales en términos de tensiones y una visión de las vulnerabilidades de la sección.

Supuestos generales de diseño e hipótesis de cálculo para el Estado Límite Último

1. La deformación ε en la armadura y el hormigón se supondrá directamente proporcional a la distancia desde el eje neutro (las secciones planas permanecen planas).
2. La interacción de la armadura y el hormigón se garantiza mediante la interacción del hormigón y la armadura sin deslizamiento (la deformación ε soporta la deformación en las fibras adyacentes del hormigón son iguales).
3. La resistencia a tracción del hormigón se desprecia (todas las tensiones de tracción se transmiten por la armadura).
4. Las tensiones de compresión del hormigón en la zona de compresión se calculan en relación con la deformación calculada a partir de los diagramas tensión-deformación.
5. Las tensiones de la armadura se calculan en función de la deformación a partir de los diagramas tensión-deformación.
6. La deformación de compresión del hormigón con un límite de deformación última _εcu2 (diagrama parábola-rectángulo para hormigón sometido a compresión) y _εcu3 (relación bi-lineal tensión-deformación),[2].
7. La deformación a compresión de la armadura es ilimitada en el caso de la rama superior plástica horizontal, en el caso de la rama superior plástica inclinada la deformación está limitada _εud,[2].
8. Se considera un estado límite cuando el estado de al menos uno de los materiales supera la deformación límite última (si εu no está limitada, rige el hormigón comprimido).

\[ \textsf{\textit{footnotesize{\qquad Tensión de deformación.}}]

\Diagrama de diseño tensión-deformación para acero de refuerzo con rama superior inclinada.

Diagrama de interacción

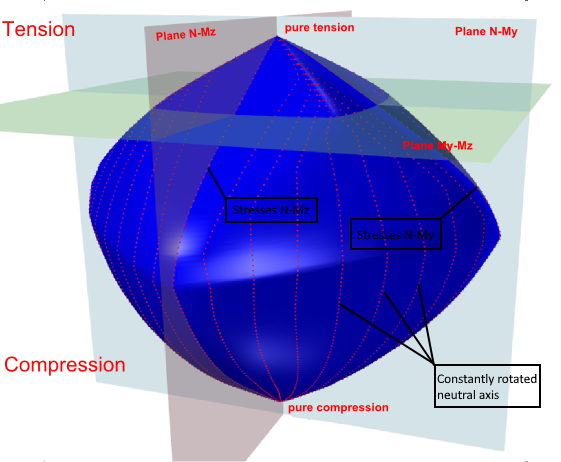
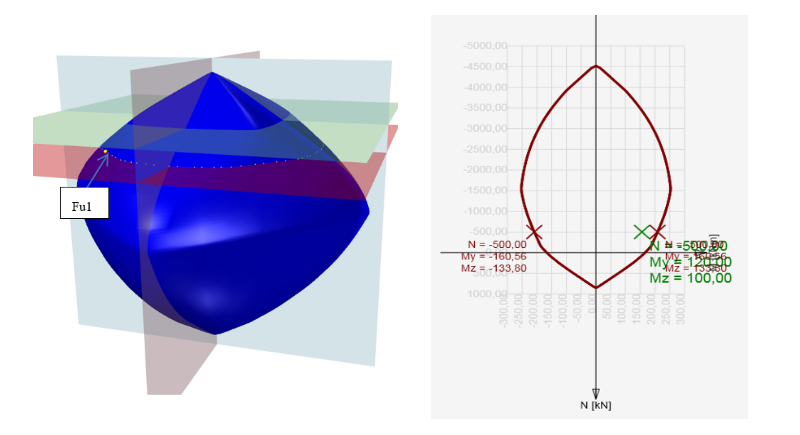
La primera opción es comprobar la sección transversal mediante una superficie de interacción (o diagrama de interacción). En la figura siguiente se ofrece una explicación sobre una muestra de las superficies de interacción para la sección cuadrada reforzada del ejemplo. En la superficie de interacción se sitúan los puntos que definen el estado límite último de la sección transversal examinada.La superficie de interacción se dibuja a partir de los puntos (N, My, Mz), que vienen determinados por la integración de tensiones en la sección transversal, que ha alcanzado la deformación límite última en uno de los materiales.Para una interacción 3D, la superficie puede derivarse de un diagrama de interacción 2D, que es una curva cerrada, que corresponde a la tensión de un eje neutro girado constantemente.

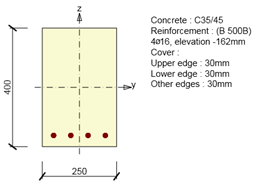
\Sección transversal reforzada simétrica.

\La superficie de interacción muestra las condiciones de fallo para todos los casos de carga de fuerza normal y momentos flectores.

Para el caso de una sección transversal simétrica alrededor del eje y, el diagrama de interacción es simétrico alrededor del plano _N-My. Del mismo modo, para el caso de una sección transversal simétrica alrededor del eje z, el diagrama de interacción es simétrico alrededor del plano _N-Mz. La sección reforzada unilateral introduce una forma aplanada del diagrama de interacción.

\[ \textsf{\textit{\footnotesize{\qquad Sección transversal reforzada simétrica unilateral.}}]

\Superficie de interacción para la sección transversal con refuerzo simétrico simple.

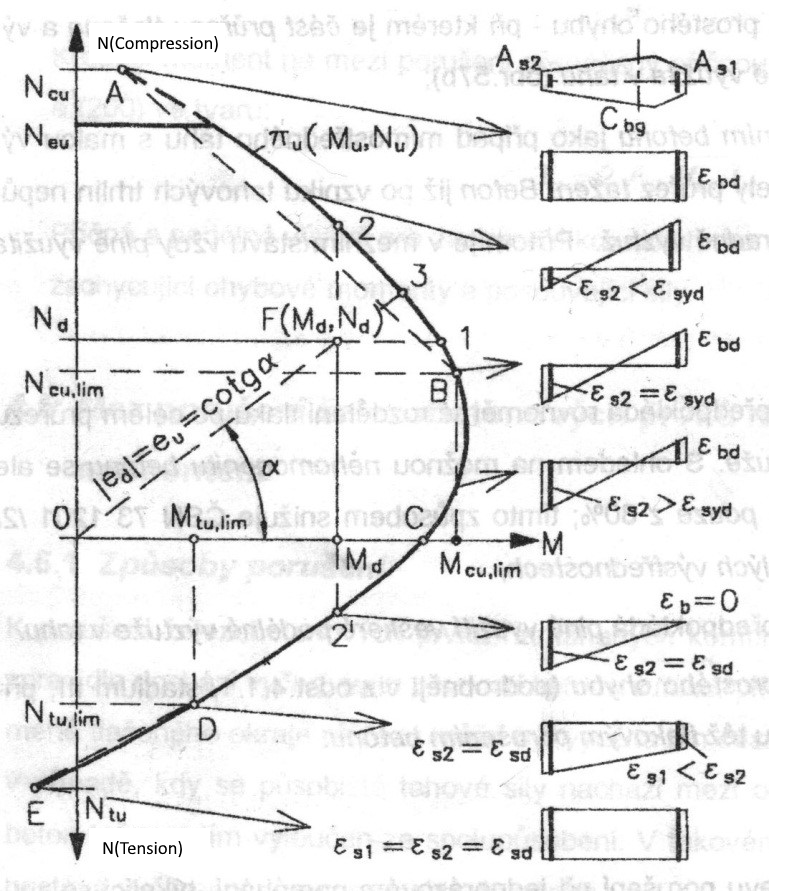
Los puntos que definen el estado límite último se obtienen de la integración de tensiones. La siguiente figura muestra la deformación en el estado límite último.

Distribuciones de deformación en el estado límite último (tomado de [2]).

El diagrama de interacción muestra el fallo de la sección transversal bajo fuerza normal y momentos flectores. [1]

Respetando el problema del diagrama 2D (curva cerrada situada sobre la superficie de interacción) podemos averiguar que el plano de deformación pasa por el eje neutro y el punto crítico [y, z, ε], que se considera como punto crítico R. El punto [y, z] define un punto de la sección transversal con el valor de deformación ε en el estado límite último. La inclinación del eje neutro es constante para todos los puntos del diagrama 2D.

En caso de que el esfuerzo de compresión en el hormigón sea crítico para el diseño, el punto R coincide con la fibra de hormigón más comprimida o con el punto límite C. Sin embargo, esto sólo puede aplicarse si esa sección está hecha de un tipo de hormigón, no como una sección transversal mixta.

En el caso de que la tensión de tracción en la armadura sea crítica para el cálculo (se supera la deformación _εud en el estado límite último para una o más barras), debe cumplirse la condición de que para el plano de deformación dado no se supere el valor _εud en ninguna otra barra.

\Utilización óptima del material de la sección transversal.

\Posiciones características del plano de deformación calculadas para el diagrama de interacción.

La imagen anterior muestra que el diagrama puede dividirse en dos partes: la parte en la que el fallo se produce por una fuerza de tracción y la parte que falla por una fuerza de compresión.Los puntos límite corresponden al caso anterior, donde también se aprecia la inclinación extrema del plano de deformación.Al dibujar un diagrama de interacción, la inclinación del plano de deformación de una sección transversal cambia en este intervalo, mientras buscamos el punto R (véase más arriba). Basándonos en ese plano definido realizamos la integración para obtener la tensión en el estado límite último.

Comprobación de la sección transversal sometida a un esfuerzo axil y a un momento flector

La comprobación de una sección sometida a un esfuerzo axil y a un momento flector se basa en probar que las tensiones comprobadas (combinación _Nd,_Myd, _Mzd) se encuentran dentro o en la zona de interacción superficial. El siguiente ejemplo muestra la comprobación de una sección rectangular sometida a fuerzas Nd₌ -500 kN,_Myd = 120 kNm, _Mzd = 100 kNm.

Método NuMuMu

Para definir la resistencia de una sección transversal suponemos cambios proporcionales en todos los componentes de la fuerza interna (la excentricidad de la fuerza normal permanece constante) hasta que se haya desarrollado la superficie interactiva.El cambio de las fuerzas internas implicadas puede interpretarse como un desplazamiento a lo largo de una líneaque une el sistema de coordenadas inicial (0,0,0) y el punto definido por las fuerzas internas (_NEd,_MEd,y,_MEd,z).Las dos intersecciones de esta línea con la superficie de interacción, que pueden encontrarse, representan dos conjuntos de fuerzas en el estado límite último. En cada intersección, el programa determina tres fuerzas en el estado límite: la resistencia de la fuerza axil de cálculo _NRd y los correspondientes momentos de resistencia de cálculo_MRdy,_MRdz.

Método NuMM

Para definir la resistencia de la sección transversal suponemos una fuerza normal constante (que es igual a la fuerza normal de cálculo actuante) y cambios proporcionales en los momentos flectores hasta que se haya desarrollado la superficie interactiva.El cambio de las fuerzas internas implicadas puede interpretarse como un desplazamiento en un plano horizontal a lo largo de la línea que une el punto (_NEd,0,0) y el punto definido por las fuerzas internas actuantes (_NEd,_MEd,y,_MEd,z).Las dos intersecciones de esta línea con la superficie de interacción, que puede encontrarse, representan dos conjuntos de fuerzas en el estado límite último. En cada intersección el programa determina tres fuerzas en el estado límite: los momentos resistentes de cálculo_MRdy,_MRdz y la (correspondiente) fuerza normal de cálculo actuante_NEd.

Método NMuMu

Para definir la resistencia de la sección transversal asumimos una fuerza normal constante (que es igual a la fuerza normal de cálculo actuante) y cambios proporcionales en los momentos flectores hasta que se haya desarrollado la superficie interactiva.El cambio de las fuerzas internas implicadas puede interpretarse como un desplazamiento en un plano horizontal a lo largo de la línea que une el punto (_NEd,0,0) y el punto definido por las fuerzas internas actuantes (_NEd,_MEd,y,_MEd,z).Las dos intersecciones de esta línea con la superficie de interacción, que pueden encontrarse, representan dos conjuntos de fuerzas en el estado límite último. En cada intersección, el programa determina tres fuerzas en el estado límite: los momentos resistentes de cálculo_MRdy,_MRdz, y la (correspondiente) fuerza normal de cálculo actuante_NEd.

Determinación de la respuesta de la sección

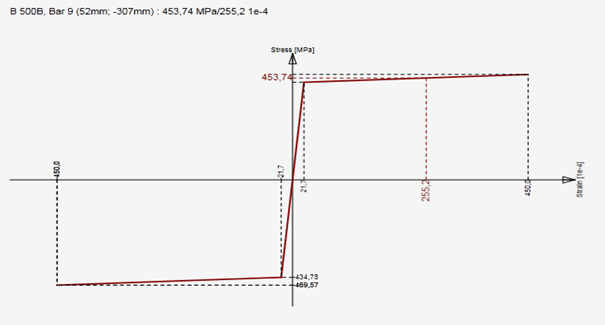
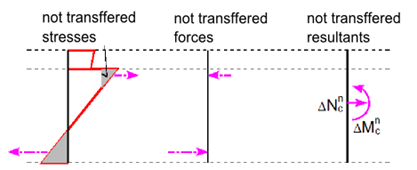
Otra posibilidad para comprobar la sección es hallar la respuesta de la sección (es decir, la distribución de deformaciones y tensiones a partir de las fuerzas internas actuantes). Este método también se conoce como método de deformación límite.El nivel de tensiones actuantes en cada fibra (en el caso de flexión plana en cada capa) encada barra reforzada se calcula en función de la deformación del diagrama Tensión-Deformación del material.
La respuesta de la sección transversal se calcula mediante el método numérico especificado en[6]. El principio consiste en el incremento gradual de la carga de la sección por las componentes desequilibradas de las fuerzas no transferidas. Éstas se obtienen integrando la tensión sobre la sección utilizando los diagramas Tensión-deformación.Si se puede encontrar el valor de la tensión para la deformación en el diagrama Tensión-Deformación, véase la figura siguiente (a), la tensión calculada es correcta suponiendo un material elástico lineal.En los casos (b) y(c), la tensión para un cálculo lineal alcanza valores irreales, y parte (b) o todo el valor (c) no pueden ser transmitidos por el material. Integrando las tensiones no transmitidas obtenemos las fuerzas internas no transmitidas, y sus resultantes deben sumarse a las fuerzas internas de las cargas variables.

Tensiones no transferidas en los diagramas Tensión-Deformación [4].

Fuerzas internas no transferidas.[4]

Este método de cálculo requiere el uso de métodos numéricos para integrar la tensión sobre el área de la sección transversal y para el análisis no lineal de las ecuaciones de equilibrio en la sección. La iteración finaliza cuando se cumplen los criterios de convergencia.

\[\frac{{F_e}} - {F_i}}{{{F_e}} \le max\left\{ {e,d} \right\}].

donde

_{Fe es la} carga de sección,

_{Fi es} la respuesta de la sección (fuerzas internas calculadas en la base del plano de deformación).

Si a es el valor aproximado (aproximado) y b es el valor exacto (verdadero), la desviación absoluta viene dada por la siguiente ecuación.

\[e = \left| {b - a} \right||]

La desviación relativa viene dada por la siguiente fórmula:

\[d = \left| {\frac{{b - a}}{b}} \right|\\]

En la mayoría de los programas, puede establecer estos criterios de convergencia (los valores por defecto son 1%como error relativo, 100 N, 100 Nm como error absoluto de la fuerza normal y momentos).

Así que si tenemos la entrada de N = 0 kN, My = 100 kNm, Mz= 0 kNm y las fuerzas integradas después de la iteración N = - 0.07 kN, My = 100,5 kNm, Mz = 0,02 kNm, la evaluación será la siguiente. Respetando que N y Mz sean iguales a 0, se puede hacer una comparación con desviación absoluta:

El valor de la fuerza normal 100N> | 70 | N
El valor del momento flector Mz 100Nm> | 20 | Nm
El valor del momento flector My

\[d = \left| {\frac{{b - a}}{b}} \right| = \frac{100 - 100,5}{100}} = 0,005\; < 0,01\]

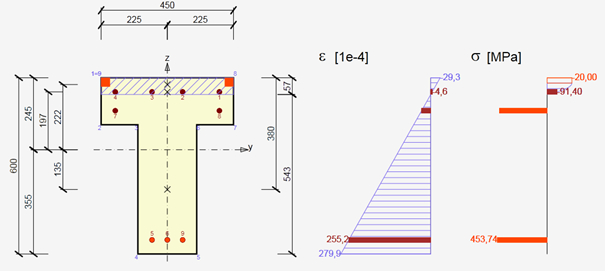
Comprobación transversal por la respuesta

En el caso de encontrar un equilibrio en la sección transversal, se conoce la deformación plana.A partir de la deformación plana, podemos calcular la deformación en cualquier punto de la sección y, a continuación, la tensión o las fuerzas internas en las barras de refuerzo, la sección transversal o sus partes utilizando los diagramas de tensión-deformación de los materiales. Los valores calculados de tensión y deformación se comparan con el valor límite de deformación de los diagramas de tensión-deformación de los materiales utilizados.
La ventaja de este método es que obtenemos una imagen completa de los valores de tensión y deformación en la sección de las fuerzas internas que actúan sobre la sección transversal.