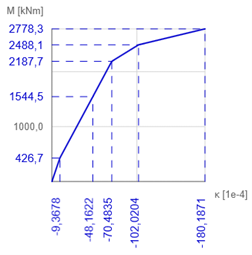
El diagrama N-M-κ muestra la curvatura de un elemento (rigidez a la flexión) en función de un momento flector y una fuerza normal aplicados. Existen tres tipos de diagramas N-M-κ:
- a corto plazo,
- a largo plazo
- ULS.
Estos diagramas difieren en los tipos de diagramas tensión-deformación utilizados para el cálculo (explicados a continuación).
El cálculo de la rigidez para los estados característicos seleccionados de la sección transversal se utiliza para determinar el diagrama N-M-κ. En general, puede ser cualquier estado de la sección transversal a partir del cual se calcula la respuesta y del que se derivan la rigidez a flexión y la curvatura. En IDEA RCS, consideramos cuatro puntos característicos (Mr,Mc,Ms yMu)
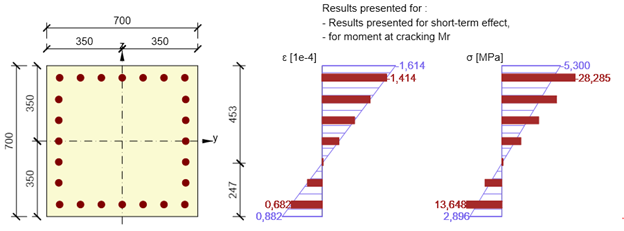
Mr - el momento de fisuración
La sección transversal se somete a una fuerza normal definida por el usuario y el plano de deformación comienza a girar (en la dirección del momento de flexión especificado) hasta que se alcanza la resistencia última a la tracción del hormigón en una fibra de hormigón (para el grado de hormigón C30/37 es fctm = 2,896 MPa). Para el cálculo se utiliza un diagrama de tensión-deformación bilineal con una rama plástica horizontal tanto para la armadura como para el hormigón.
Mc - el momento flector cuando se alcanza la resistencia a la compresión del hormigón
A partir del paso anterior, se identifica la fibra de hormigón más utilizada en compresión. Para esta fibra, se establece la deformación a la resistencia última del hormigón (fck/Ecm para corto plazo, fck/Eceff para largo plazo y fcd/Ecm para el diagrama ULS). A partir de la fuerza normal definida y la dirección del momento flector, se ejecuta el proceso de iteración para encontrar el plano de deformación con el fin de encontrar un equilibrio entre la respuesta de la sección transversal y la fuerza normal definida. Para el cálculo se utiliza un diagrama de tensión-deformación bilineal con una rama plástica horizontal tanto para la armadura como para el hormigón.
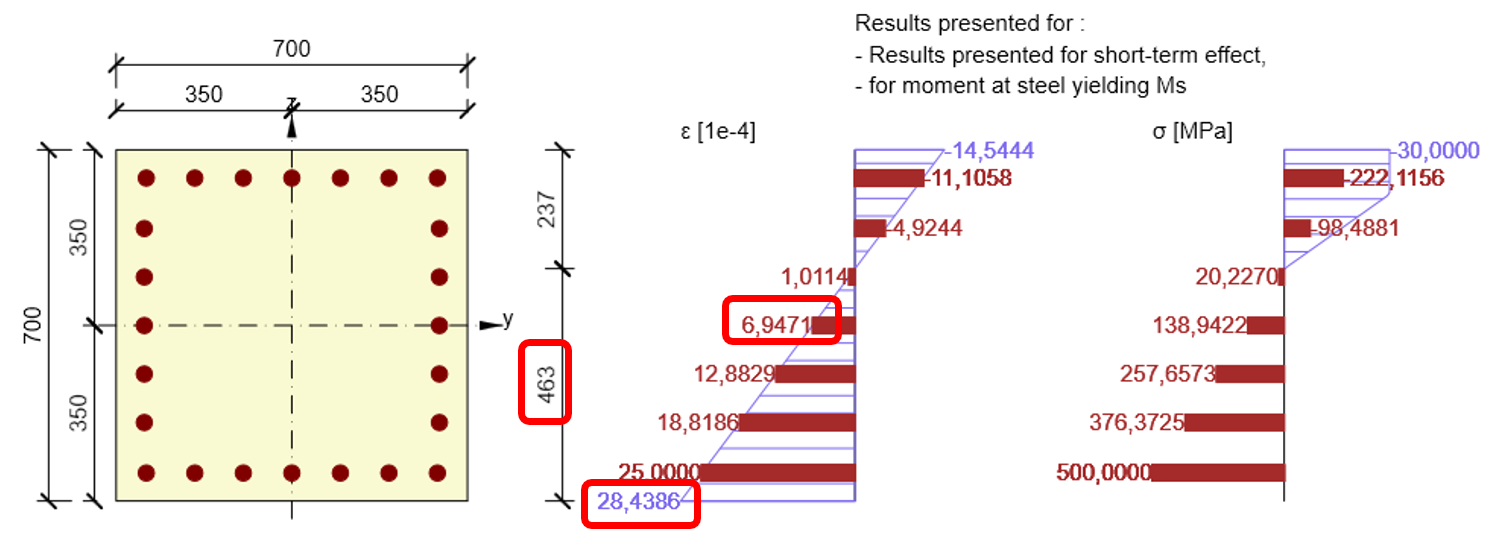
Ms - el momento flector cuando se alcanza el límite elástico en la barra de refuerzo más utilizada
Otro punto característico del diagrama N-M-κ es el estado tensional de la sección transversal cuando se alcanza el límite elástico en la barra de armadura más utilizada (la deformación de la armadura es igual a fyk/Es para los diagramas a corto y largo plazo, fyd/Es para el diagrama ULS). El proceso de iteración encuentra un equilibrio de fuerzas normales en la sección transversal girando el plano de deformación alrededor del punto especificado por la posición de la barra de refuerzo más utilizada. Para el cálculo se utiliza un diagrama tensión-deformación bilineal con una rama plástica horizontal tanto para la armadura como para el hormigón.
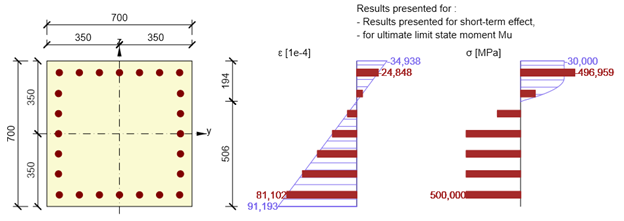
Mu - el momento flector en el estado límite último
Es la capacidad de carga última de una sección transversal en flexión, cuando la sección transversal está sometida a una fuerza normal de diseño definida Ned. Para el cálculo de la capacidad de la sección transversal, se supone que se alcanza la resistencia a la compresión en la fibra de hormigón más utilizada y la resistencia a la tracción en la barra de armadura más utilizada (deformación máxima para el hormigón εcu = 0,1 y para la armadura εs,max = 0,5). Para el cálculo se utiliza un diagrama tensión-deformación bilineal con una rama plástica horizontal para la armadura y un diagrama parábola-rectangular para el hormigón.
La rigidez y la curvatura resultantes debidas a la combinación definida por el usuario de fuerza normal y momento flector ( Md) se calculan a continuación mediante interpolación lineal de los puntos característicos individuales del diagrama N-M-κ.
Cálculo de rigideces y curvaturas
Las rigideces y curvaturas para cada estado de tensión transversal (Mr,Mc,Ms oMu) se calculan directamente a partir de la rotación del plano de deformación.
\[E{{A}_{x}}=\frac{N}{{{\varepsilon }_{x}}}\]
EAx. . rigidez axial del elemento
N . . . la fuerza normal especificada
εx. . . deformación axial en el centro de gravedad de la sección transversal de hormigón
\[E{{I}_{y}}=\frac{M}{\kappa }\]
EIy. . . rigidez a flexión del elemento
M . . . el momento flector calculadoMr,Mc,Ms oMu
κ . . . . la curvatura del elemento, calculada como la tangente del ángulo entre el plano de deformación y el eje longitudinal del elemento
Ejemplo práctico
Una sección transversal de hormigón (grado de hormigón C30/37) se refuerza con ϕ32 armaduras (grado B500B). La combinación cuasipermanente definida es N = -730 kN yMy = 557 kNm.
El plano de deformación para el punto característicoMs se determina mediante IDEA RCS de la siguiente manera:
\[E{{A}_{x}}=\frac{N}{{{\varepsilon }_{x}}}=\frac{730}{6,9471\cdot {{10}^{-4}}}=1050,798MN\]
\[\kappa =\frac{28,4386\cdot {{10}^{-4}}{0,463}=61,422\cdot {{10}^{-4}}{{m}^{-1}}]
\[E{{I}_{y}}=\frac{{{M}_{s}}}{\kappa }=\frac{2277,4}{61,422\cdot {{10}^{-4}}}=370,776MN{{m}^{2}}\]
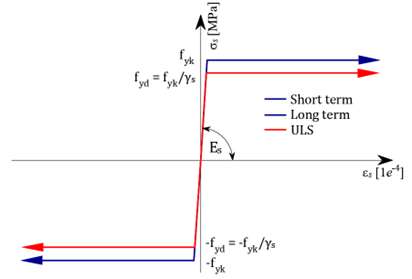
Diagramas tensión-deformación utilizados para el cálculo
Refuerzo -Mr,Mc,Ms yMu
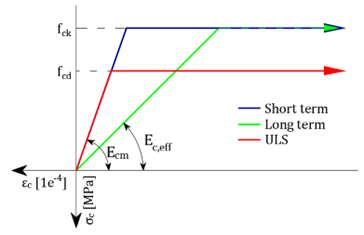
Hormigón -Mr,Mc,Ms
Hormigón -Mu