Con respecto al fallo por fragilidad, la comprobación del esfuerzo cortante es una de las comprobaciones importantes de una sección de hormigón armado.
Procedimiento de cálculo
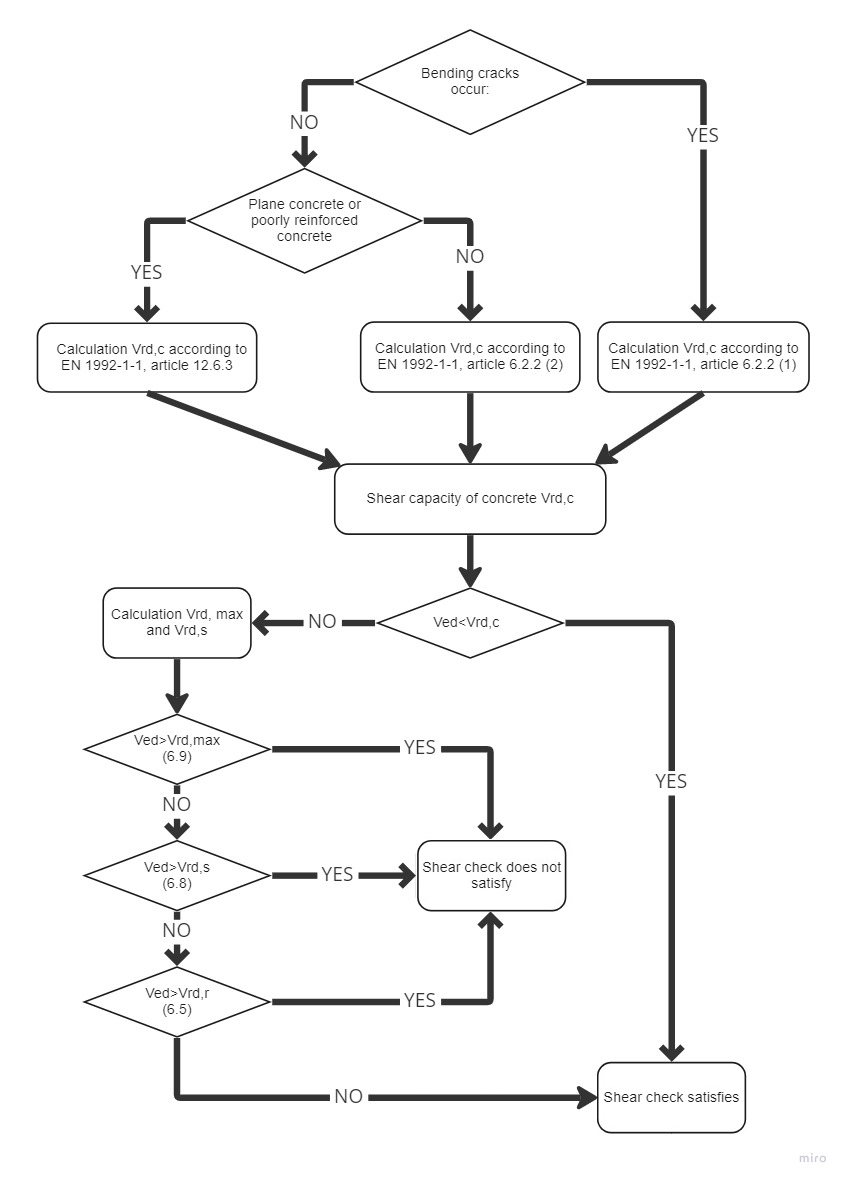
El cálculo de la resistencia a cortante se compone de varias partes básicas. En primer lugar se debe analizar si se producen o no fisuras por flexión en el lugar comprobado.Si las hay, se utiliza el cálculo según la norma EN 1992-1-1[2], artículo 6.2.2 (1).En caso contrario, determinamos si se trata de hormigón plano o poco armado, y procedemos según la norma EN 1992-1-1, artículo 12.6.3.
Para el hormigón armado no fisurado (sin armadura de cortante) comprobamos según EN 1992-1-1 Artículo 6.2. (2).En el caso de elementos que requieran armadura de cortante, se comprobará de acuerdo con el artículo 6.2.3[2].
\Diagrama de proceso para la comprobación a cortante.
Resistencia a cortante de elementos sin refuerzo a cortante
Resistencia a cortante de elementos en zonas de flexión fisurada (art. 6.2.2 (1)[2])
La resistencia a cortante de elementos de hormigón armado sin armadura de cortante sometidos a momento flector viene dada por:
\[{{V}_{Rd,cm}}=~{{C}_{Rd.c}}k~{{\left( 100~{{\varrho }_{l}}{{f}_{ck}} \right)}^{{}^{1}/{}_{3}}}~{{b}_{w}}d\]
Que se definió a partir de los ensayos realizados en un número representativo de vigas simples en caso de fallo por esfuerzo cortante. Dado que la resistencia anterior puede ser cero para los elementos sin refuerzo longitudinal (rl), para los miembros poco reforzados se derivaron ecuaciones. Dado que la resistencia anterior puede ser cero para los elementos sin refuerzo longitudinal (rl), para los miembros mal reforzados se determinó mediante la ecuación
\[{{V}_{Rd,c}}ge ~{{{upsilon }_{min}}{{b}_{w}}d\]]
Para la resistencia a cortante con influencia de la fuerza normal se determinó mediante la ecuación
\[{{V}_{Rd,cn}}=~{{k}_{1}}{{\sigma }_{cp}}~{{b}_{w}}d\]
Resistencia al cizallamiento en su expresión completa que se corresponde con EN 1992-1-1 art. 6.2.2 (1)
\[{{V}_{Rd,c}}=~{left[ {{C}_{Rd.c}}k~{{left( 100~{{varrho }_{l}}{{f}{ck}} \right)}^{{}^{1}/{}_{3}}+{{{k}_{1}{{sigma }_{cp}}{right} \...]~{b}_{w}d]
Con un mínimo de
\{{V}_{Rd,c}}=~\left( {{\upsilon }_{min}}+{{k}_{1}}{{sigma }_{cp}} {right){{b_{w}d]
donde
CRd,c = 0,18 / γc,
k factor de altura de la sección transversal
\[k=1+\sqrt{\frac{200}{d}}<2,0\]
ρ1 coeficiente de refuerzo de la armadura longitudinal
\[{{\varrho }_{l}}=\frac{{{A}_{sl}}}{{{b}}d}}le 0,02\]
fck resistencia cilíndrica a la compresión característica del hormigón a 28 días
k1 = 0,15
σcp =NEd /Ac < 0,2 fcd v MPa
bw anchura mínima de la sección transversal en la zona de tracción
d profundidad efectiva de una sección transversal
υmin resistencia mínima al cizallamiento equivalente υmin = 0,035 k3/2 fck1/2
Resistencia a cortante de los elementos en zonas de flexión no fisuradas (art. 6.2.2 (2)[2])
La resistencia a cortante de los elementos en zonas de flexión no fisuradas puede determinarse a partir del círculo de Mohr. En la ecuación
\[{{sigma }_{1,2}}=\frac{{{sigma }__{x}}+{{sigma }_{y}}{2}pm \sqrt{{{left( \frac{{sigma }_{x}}-{{sigma }__y}}{2}{right)}^{2}}+\tau _{z}^{2}}].
Sustituimos σx = σcp a τz= VRd,c S / (I bw) y calculamosVRd,c y obtenemos la ecuación correspondiente con la fórmula dada en EN 1992-1-1 art. 6.2.2 (2)
donde
I es el segundo momento del área,
bw es la anchura de la sección transversal en el eje centroidal
S es el primer momento del área por encima y alrededor del eje centroidal,
fctd resistencia a la tracción axial de diseño del hormigón en MPa,
scp es el esfuerzo de compresión del hormigón en el eje centroidal debido a la carga y/o al pretensado,
al factor de longitud de transmisión, normalmente 1,0.
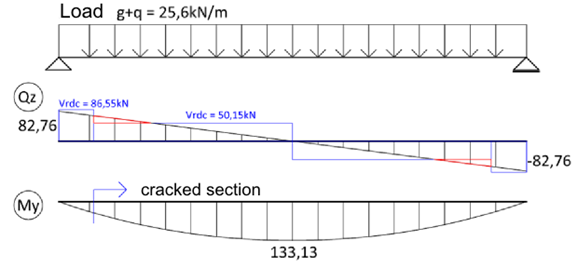
En relación con lo anterior, debe tenerse en cuenta que en zonas sin fisuras por flexión laresistenciaVRd ,c puede ser significativamente mayor que en las zonas agrietadas según el artículo 6.2.2 (1)[2]. La figura siguiente muestra claramente que aunque el esfuerzo cortante se verifique en su extremo (que no produce fisuras), no tiene por qué garantizar que se transmita a lo largo de toda la longitud de la viga.Esto se debe a un cambio en el método de cálculo de la resistencia al cizallamiento del hormigón.Por supuesto, la resistencia al cizallamiento puede considerarse según el artículo 6.2.2 (1)[2] también en lugares donde no se producirán fisuras.
\Comparación de la resistencia al corte antes y después de la aparición de grietas.
A la expresión deVRd, c según el artículo 6.2.2 (2)[2] también debe tenerse en cuenta que en el caso general debe basarse en la comprobación en la fibradel esfuerzo de tracción principal extremo del hormigón en la zona del esfuerzo de compresión normal, pero no en el centro de gravedad de la sección.En este punto es necesario calcular las características de la sección transversal (S y bW).Para determinar la tensión principal máxima s1 en el programa IDEA RCS trazamos una línea a través del centro de gravedad en la dirección de los esfuerzos cortantes resultantes.Esta línea la dividimos en 20 sectores. En esta línea presentaremos más puntos característicos (puntos del polígono de la sección transversal, centro de gravedad, el eje neutro).Dentro de estos puntos, calculamos S, bw, σx, τyz a σ1. En el punto de máxima tensión principal de tracción calcularemos la resistencia al cizallamiento.
El esfuerzo cortante antes de aplicar el factor de reducción b exigido por el artículo 6.2.2 (6) debe cumplir la condición adicional
\[ {{V}_{Ed}}le 0,5~{{b}_{w}}d~\upsilon ~{{f}_{cd}}]
donde
\ [ {{ υ}}\le 0,6\left[ 1-\frac{{f}_{ck}}}{250} \right]\] kde fck je v MPa
Resistencia a cortante de elementos sin armadura o ligeramente armados (art. 12.6.3[2])
La resistencia a cortante para hormigón liso o ligeramente armado puede determinarse a partir de la expresión
\[ {{\tau }_{cp}}le k~{{V}_{Ed~}}/{{A}_{cc}}]
Donde
τcp lo sustituimos por
\[ {{f}_{cvd}}={sqrt{f_{ctd,pl}^{2}+{{\sigma }_{cp}}{f}_{ctd,pl}}~pro~{{sigma }_{cp}}le {{sigma }_{c,lim}}~]
o
\{ {{f}_{cvd}={sqrt{f_{ctd,pl}^{2}+{{{sigma }_{cp}}{f}_{ctd,pl}}-{left( {frac{{sigma }_{cp}}-{{{sigma }_c,lim}}{2}{right)}^2}}~{pro~{{sigma }_{cp}}>{{{sigma }_{c,lim}}~]
Los valores parciales utilizados en la fórmula anterior vienen dados por:
\{{{sigma }_{c,lim}}={{f}_{cd,pl}}-2{sqrt{{{f}_{ctd,pl}}left( {{f}_{ctd,pl}}+{{f}_{cd,pl}} \right)}}.
donde
fcd,pl Resistencia a compresión de diseño para hormigón simple o poco armado,
fctd,pl Resistencia a la tracción axial calculada para hormigón simple o poco armado,
fcvd Resistencia de cálculo a cortante bajo compresión del hormigón.
Resistencia de elementos con armadura de cortante (art. 6.2.3[2])
El cálculo de la resistencia de elementos de hormigón armado con armadura de cortante se basa en el método de analogía de celosía con diagonales de ángulo variable.La base de este método es el equilibrio de fuerzas en el triángulo determinado por la fuerza del puntal (diagonal), la fuerza de la armadura de cortante (estribo) y la fuerza de la armadura longitudinal.
\[ \textsf{\textit{\footnotesize{qquad Principio de la analogía de Truss para miembro bajo carga de cortante.}}]
La sección transversal bajo carga de corte se rompe por las grietas en un ángulo θ, por esta razón la diagonal de hormigón con el mismo ángulo que las fuerzas de corte está resistiendo a la fuerza de corte. La fuerza de compresión de la diagonal se puede expresar como Ved/sinθ. Esta fuerza debe ser transferida por la superficie del hormigón, perpendicular a la diagonal de compresión bwzcosθ. El esfuerzo de tensión del hormigón en la diagonal de compresión es entonces igual:
\[ {{sigma }_{c}}={frac{{V}_{Ed}}{{b}{w}}z~sin \text{ }!\!\theta!\text{ }cos \theta }={frac{{V}_{Ed}}{{b}{w}}z}left( \tan \theta +\cot \theta \right)\}].
Sustituyendo "sigma" por "alfa" y " V"... y expresando \ [{{V}_{Rd,max}} obtenemos la ecuación para la resistencia al corte de la diagonal:
\[ {{V}_{Rd,max}}=~{\\alpha }_{cw}}~{{b}_{w}}~z~{{\nu }_{1}}{{f}{cd}}/left( \cot \theta +\tan \theta right)\}]
Para equilibrar el componente de fuerza vertical en la diagonal de compresión, se utilizará un refuerzo de cortante.El tamaño de la fuerza vertical se basa en la tensión de compresión diagonal en elEl tamaño de la fuerza vertical se basa en la tensión de compresión diagonal en el área del hormigón que corresponde a un estribo - \ [{{sigma }_{c}}{{b}}_{w}}s{{sin }^{2}}\theta\]. La fuerza límite del estribo viene dada por \ [{{A}_{sw}}{{f}_{ywd}}/s].
Insertando σc, comparando con la fuerza límite en la armadura, tras las modificaciones obtenemos:
\[ \frac{{{A}_{sw}}{{f}_{ywd}}}{s}=\frac{{{V}_{Ed}}}{z}\tan \theta\]
Entonces expresando Ved comoVRDs obtenemos la resistencia de la sección transversal con refuerzo de cortante vertical:
\[ {{V}_{Rd,s}}=~\frac{{{A}_{sw}}}{s}z~{{f}_{ywd}}\cot \theta\]
El esfuerzo cortante longitudinal es transferido por la armadura longitudinal y puede determinarse como Vedcotgθ. La derivación de las fórmulas anteriores puede encontrarse en[4].
Utilizando el programa IDEA RCS es posible comprobar sólo las barras con armadura de cortante vertical. En general se pueden utilizar las siguientes ecuaciones:
\[{{V}_{Rd,s}}=~\frac{{{A}_{sw}}}s}z~{{f}_{ywd}}left( \cot \theta +\cot \alpha \right)\sin \alpha]].
\{{V}_{Rd,max}}=~{\\alpha }_{cw}}~{{b}_{w}}~z~{{\nu }_1}}{{f}{cd}}left( \cot \theta +\cot \alpha \right)/\left( 1+{\cot }^{2}}\theta \right)\}
Donde
Asw es el área transversal de la armadura de cortante,
s es la separación de los estribos,
fywd es el límite elástico de diseño del refuerzo para esfuerzo cortante,
bw es la anchura mínima entre los cordones de tracción y compresión. Para calcular la resistenciaVRd,max , el valor de la anchura de la sección debe reducirse a la denominada anchura nominal de la sección transversal en caso de que la sección transversal esté debilitada por conductos de cables
bw,nom=bw-0,5ΣΦ para conductos metálicos rejuntados
bw,nom=bw-1,2ΣΦ para conductos metálicos sin rejuntado
υ = 0,6 pro fck ≤ 60MPa o pro fck > 60MPa,
αcw es un coeficiente que tiene en cuenta el estado de la tensión en el cordón de compresión.
| Carga | σcp = 0 | 0 <σcp≤0,25fcd | 0,25fcd <σcp≤0,5fcd | 0,5fcd <σcp≤1,0fcd |
| Coeficienteacw | 1,0 | 1+σcp/fcd | 1,25 | 2,5(1 - σcp/fcd) |
Tab. 1-1 Coeficiente determinante αcw
El ángulo θ es el ángulo entre el puntal de compresión del hormigón y el eje de la viga perpendicular al esfuerzo cortante. Los valores límite de cotθ para su uso en un País pueden encontrarse en su Anexo Nacional. Los límites recomendados vienen dados por la expresión
\[1~\le ~\cot \theta \le 2,5\]
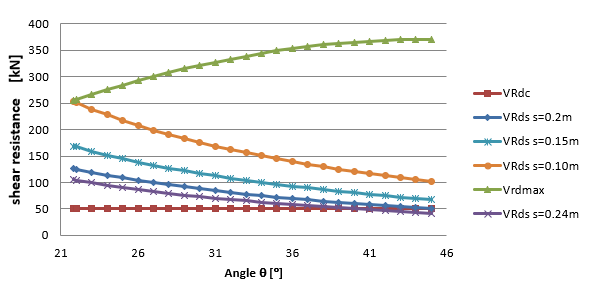
14. La elección del tamaño del ángulo θ puede afectar al valor de las resistencias. La dependencia de las resistencias es visible en la figura 1.15. La figura muestra que con el aumento del ángulo θ la resistenciaVRd,max aumenta, y la resistenciaVRd,s disminuye. La resistenciaVRd,c es constante, ya que se basa en el método de analogía de cerchas.
\[ \textsf{\textit{\footnotesize{\qquad Dependencia entre la resistencia a cortante y el ángulo q.}}]
Cálculo de las características de la sección transversal a cortante
Para calcular el cortante es importante calcular las variables de la sección transversal que afectan a la resistencia al cortante.Estas variables incluyen principalmente la anchura de la sección resistente a cortante bw, la profundidad efectiva d y el brazo de palanca z. El código[2] proporciona estos valores que se correlacionan directamente con el esfuerzo de flexión real.Pero el problema es determinar estos valores cuando la dirección de los momentos flectores resultantes (o más exactamentela dirección de la resultante de la resistencia de la sección) es significativamente diferente de la dirección de los esfuerzos cortantes resultantes.En este caso, el código EC2 no proporciona ninguna recomendación.
Anchura de la sección resistente a cortante bw
El programa IDEA RCS calcula la anchura de la sección transversal resistente a cortante en la dirección perpendicular a la resultante de los esfuerzos cortantes.Dependiendo del artículo del Eurocódigo, esta anchura se calcula como:
- La menor anchura de la sección entre la resultante del hormigón a compresión y la armadura a tracción en la dirección perpendicular a la resultante de los esfuerzos cortantes para el artículo 6.2.2 (a) y 6.2.3 (1)
- La anchura de la sección en dirección perpendicular a la resultante de los esfuerzos cortantes en el punto comprobado según el artículo 6.2.2 (2)
Profundidad efectiva de una sección transversal
La profundidad efectiva suele definirse como la distancia de la fibra de hormigón más comprimida al centro de gravedad de la armadura.Dado que está directamente relacionada con la flexión, la distancia se da como proyección perpendicular a la línea de gravedad de la deformación plana.
Esta definición puede aclararse de modo que en lugar del centro de gravedad de la armadura de tracción se utilice la posición de la resultante de fuerzas de la armadura.Durante el desarrollo del programa IDEA RCS se resolvió el problema decómo definir la profundidad efectiva de la sección transversal, para la que el plano de cargas de flexión no se corresponde con la dirección de las fuerzas resultantes de cizallamiento.Por lo tanto, la profundidad efectiva se define como la distancia de la fibra de hormigón más comprimida a las fuerzas resultantesen la armadura de tracción (en función del esfuerzo de flexión) y en la dirección de los esfuerzos cortantes resultantes, véase la figura 1.17.
Se producirán casos excepcionales si no podemos determinar la fibra comprimida o la resultante en la armadura de tracción. En este caso, recomendamos utilizar el valor 0.9 h (90% de la profundidad de la sección en la dirección de los esfuerzos cortantes resultantes). Este valor, el usuario puede definirlo en el programa IDEA RCS mediante el ajuste de variables de código.
Brazo de palanca de los esfuerzos internos
El brazo de palanca de los esfuerzos internos se encuentra en 6.2.3 (3)[2] y se define como la "distancia entre las cuerdas de tracción y compresión". El código no define cómo proceder cuando el plano del momento flector actuante es diferente de la dirección de los esfuerzos cortantes resultantes.Por lo tanto, como en el caso de la profundidad efectiva, definimos la distancia en la dirección de los esfuerzos cortantes resultantes.También aquí, podemos enfrentarnos a casos de excepción similares, por ejemplo, toda la sección está bajo compresión, etc. En este caso, tomamos el valor 0.9 d (90% de la altura efectiva de la sección). Este valor, el usuario puede establecerlo en el programa IDEA RCS mediante el ajuste de variables de código.
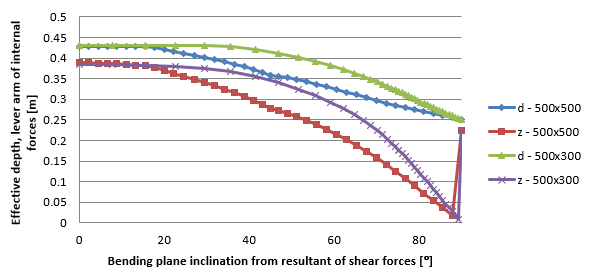
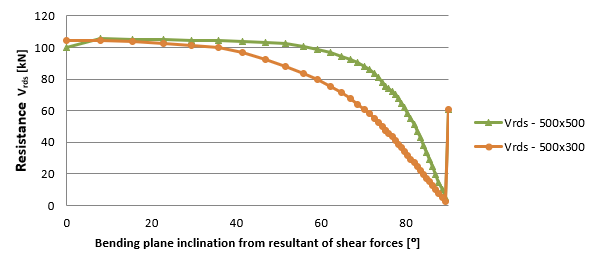
La dependencia entre la inclinación del plano de flexión y la resultante de la fuerza cortante es claramente visible en la Figura 1.18 y la Figura 1.19. Con un aumento de la inclinación del plano de flexión, la resultante de la fuerza cortante es mayor.19. Con un aumento de la inclinación, los valores de la altura efectiva, los brazos de palanca y las resistencias relacionadas disminuyen. El estado límite es 90°. Para esta inclinación no se puede calcular el brazo de palanca de las fuerzas internas, por lo que el brazo de palanca es igual a cero. En este caso, se considera el valor especificado en el ajuste de las variables del código. Este estudio demuestra que el máximo recomendado para la inclinación es de unos 20°.
\[ \textsf{\textit{\footnotesize{qquad Dependencia entre la profundidad efectiva, el brazo de palanca a la inclinación del plano de flexión y la resultante de los esfuerzos cortantes.]
\Dependencia entre la resistencia Vrds a la inclinación del plano de flexión y la resultante de los esfuerzos cortantes.
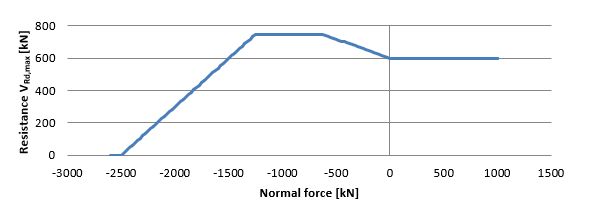
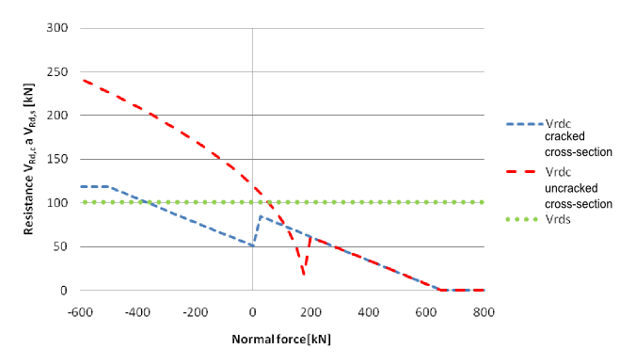
Como parte de las pruebas de la aplicación RCS, se realizó un estudio sobre la dependencia de la resistencia al cizallamiento al cambio de la fuerza normal. La resistenciaVRd,max sólo se ve afectada por el coeficiente αcw, ver Fig. 1.20. La Fig. 1.21 muestra un valor constante de la resistenciaVRds. Para la resistenciaVRdc, las disminuciones causan el aumento de la fuerza normal.La curva azul de la Fig. 1.21 muestra la resistenciaVRdc despreciando la influencia de las grietas y se calculó utilizando la fórmula de la sección 6.2.2 (1)[2]. El salto en la transición entre presión y tensión es causado por el refuerzo de tracción aportado. La curva roja se calcula utilizando la fórmula del apartado 6.2.2 (2)[2]. Después de producirse la primera fisura, la curva de dependencia es la misma que la del apartado 6.2.2 (1)[2].
\Curva de dependencia de la resistencia a cortante VRd,max a la fuerza normal.
\Dependencia de las resistencias al corte VRd,c y VRd,s con la fuerza normal.