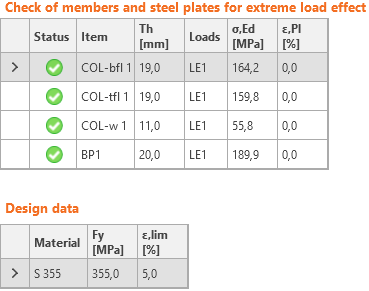
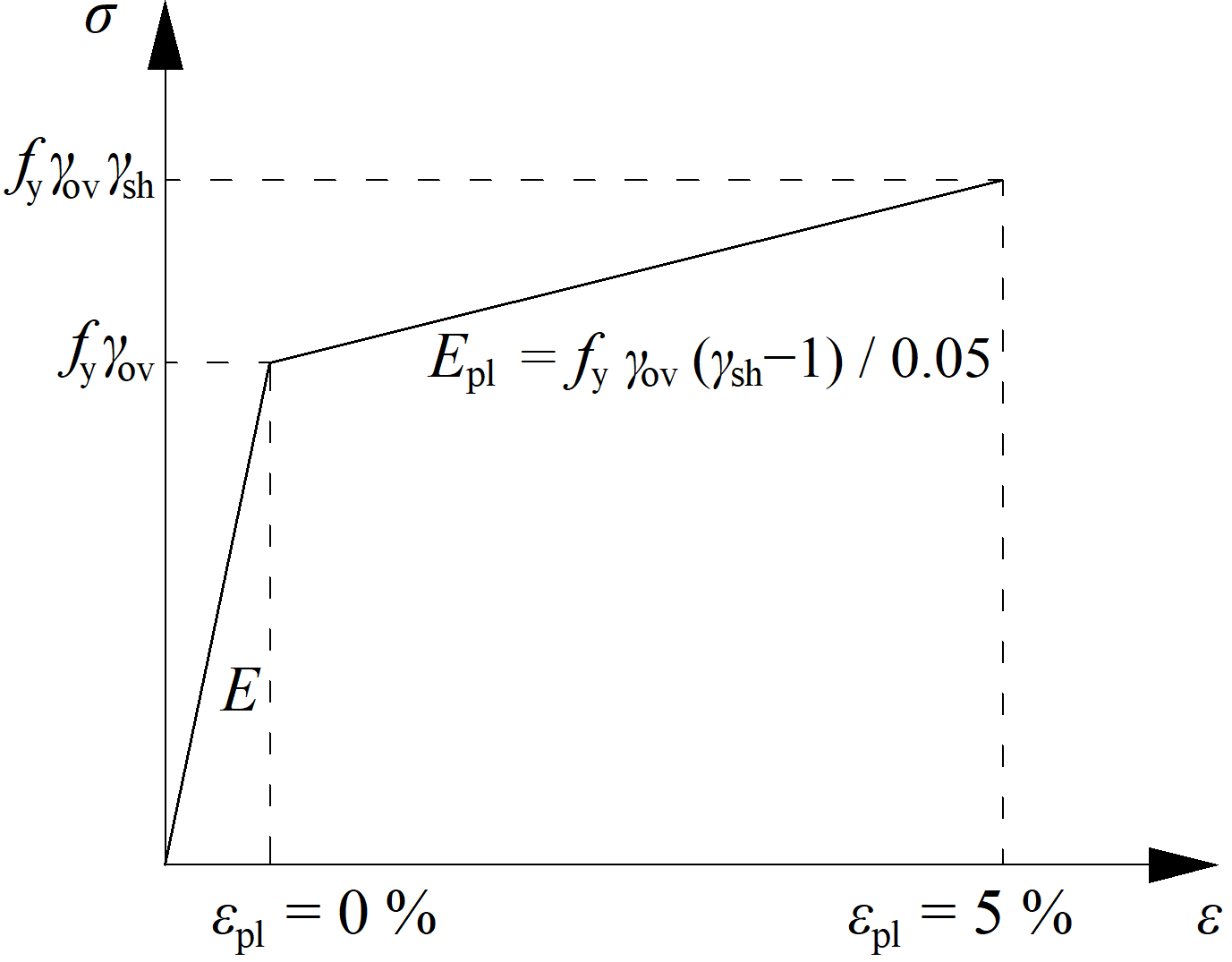Nachweis von Komponenten nach EN (Eurocode)

Die CBFEM-Methode kombiniert die Vorteile der allgemeinen Finite-Elemente-Methode (FEM) und der Standardkomponentenmethode (CM). Die anhand des genauen CBFEM-Modells berechneten Spannungen und Schnittgrößen werden beim Nachweis aller Komponenten verwendet.

Einzelne Komponenten werden nach Eurocode EN 1993-1-8 nachgewiesen.

Nachweis von Platten nach Eurocode

Die resultierende Vergleichsspannung (Huber-Mises-Hencky – HMH, von Mises) und die plastische Dehnung werden auf Platten berechnet. Für Stahlplatten wird ein elasto-plastisches Materialmodell verwendet. Es wird ein Nachweis einer äquivalenten plastischen Dehnung durchgeführt. Der Grenzwert von 5% wird im Eurocode empfohlen (EN 1993-1-5, Anh. C, Abs. C8, Anmerkung 1), dieser Wert kann vom Nutzer in den Normeinstellungen geändert werden.

Das Plattenelement wird in 5 Ebenen unterteilt und das elastische/plastische Verhalten wird in jeder Ebene separat untersucht. Die Übersicht der Ausgabe listet den kritischsten Nachweis aus allen 5 Ebenen auf.

Die CBFEM-Methode kann Spannungen ausgeben, die eher höher sind als die Streckgrenze. Der Grund ist die leichte Neigung des plastischen Zweigs des Spannungs-Dehnungs-Diagramms, das in der Berechnung zur Verbesserung der Stabilität der Interaktionsrechnung verwendet wird. Dies ist für die praktische Bemessung kein Problem. Bei höheren Belastungen steigt die äquivalente plastische Dehnung an und die Verbindung versagt bei Überschreitung der plastischen Dehngrenze.

Norm-Prüfung von Schweißnähten (EN)

Kehlnähte werden nach EN 1993-1-8 geprüft. Die Festigkeit von Stumpfnähten wird mit der des Grundwerkstoffs gleichgesetzt und nicht geprüft.

Kehlnähte

Bemessungswiderstand

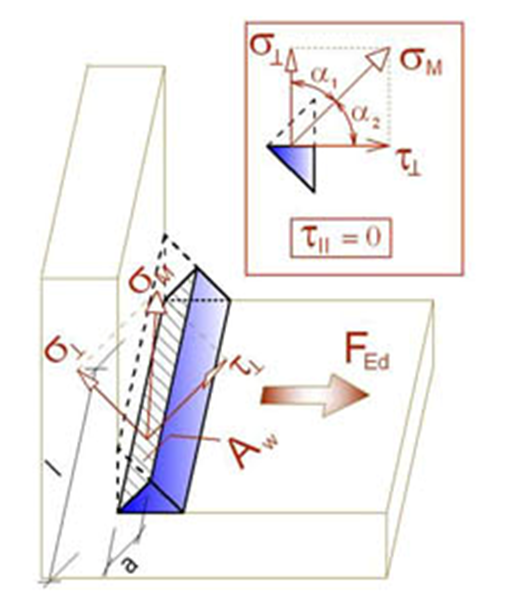
Die plastische Umverteilung in Schweißnähten wird verwendet, um Spannungssingularitäten in Schweißelementen automatisch zu vermeiden und die Spannung weiter über die Schweißnahtlänge zu verteilen. Die Festigkeit der Schweißnaht entspricht annähernd der Handberechnung, und die Spannung wird bei komplizierten Problemen wie dem Schweißen an einen unversteiften Flansch korrekt verteilt (EN 1993-1-8 - Cl. 4.10). Die Spannung im Kehlnahtbereich einer Kehlnaht wird nach EN 1993-1-8 Cl. 4.5.3. Die Spannungen werden aus den Spannungen im Schweißelement berechnet. Das Biegemoment um die Schweißnahtlängsachse wird nicht berücksichtigt.

\[ \sigma_{w,Ed}=\sqrt{\sigma_{\perp}^2 + 3 \links ( \tau_{\perp}^2 + \tau_{\parallel}^2 \rechts )} \]

\[ \sigma_{w,Rd} = \frac{f_u}{\beta_w \gamma_{M2}} \]

Schweißnahtausnutzung

\[ U_t = \min \links\{ \frac{\sigma_{{w,Ed}}}{\sigma_{w,Rd}}, \frac{\sigma_{\perp}}{0.9 f_u / {\gamma_{M2}}} \right\} \]

wobei:

• σw_,Ed - Vergleichsspannung in der Schweißnaht
• σw_,Rd - Schweißnahtwiderstand
• _βw - Korrelationsfaktor (EN 1993-1-8 - Tabelle 4.1)
• _fu - Bruchfestigkeit, gewählt als der niedrigere der beiden verbundenen Grundwerkstoffe oder entsprechend dem vom Anwender gewählten Werkstoff
• _γM2 - Sicherheitsfaktor (EN 1993-1-8 - Tabelle 2.1; editierbar im Code-Setup)
• σ_┴,τ_┴,τ‖ - Spannungen in der Schweißnaht gemäß der folgenden Abbildung:

Alle für die Prüfung erforderlichen Werte sind in Tabellen ausgedruckt. Ut ist die Verwendung des am stärksten beanspruchten Elements. Da die plastische Umverteilung der Spannungen in der Schweißnaht genutzt wird, ist dies die maßgebliche Ausnutzung. Utc gibt Auskunft über die Ausnutzung entlang der Schweißnahtlänge. Es ist das Verhältnis der tatsächlichen Spannung an allen Elementen der Schweißnaht zum Bemessungswiderstand der Spannung über die gesamte Länge der Schweißnaht.

Die Vergleichsspannung im Schweißnahtdiagramm zeigt die folgende Spannung:

\[ \sigma = \max \links \{ \frac{\sigma_{\perp}}{0.9 \beta_w}, \, \sqrt{\sigma_{\perp}^2 + 3 \tau_{\perp}^2 + 3 \tau_{\parallel}^2} \recht \} \]

Stumpfnähte

Schweißnähte können als Stumpfnähte angegeben werden. Bei Stumpfnähten wird eine vollständige Durchdringung der Naht berücksichtigt, daher werden solche Schweißnähte nicht geprüft.

Detaillierung

Die Mindestblechdicke von geschweißten Verbindungen wird gemäß EN 1993-1-8 - 4.1(1) geprüft:

• Bei Stahlhohlprofilen sollte die Blechdicke mindestens 2,5 mm betragen.
• Für andere Bleche sollte die Blechdicke mindestens 4 mm betragen.

Die maximale Schweißnahtdicke von Kehlnähten wird für parallele Bleche geprüft. Es wird eine Fehlermeldung ausgegeben, wenn eine solche Schweißnaht aufgrund geometrischer Beschränkungen nicht durchführbar ist.

Die minimale Kehlnahtdicke von Kehlnähten sollte gemäß EN 1993-1-8 - 4.5.2(2) mindestens 3 mm betragen. Ein Fehler wird ausgegeben, wenn diese Anforderung nicht erfüllt ist.

Eine Warnung wird ausgegeben, wenn die Kehlnahtdicke kleiner ist als die Anforderung in DIN EN 1993-1-8 - NA zu 4.5.2:

\[a \le \sqrt{t_{max}}-0,5\]

wobei:

• \(a\) - Dicke der Schweißnahtkehle
• \(t_{max}\) - Dicke des dickeren angeschlossenen Blechs
• Einheiten müssen in [mm] angegeben werden

Eine Information wird ausgegeben, wenn die Dicke der Schweißnahtkehle kleiner ist als die Anforderung an die Mindestduktilität von Schweißverbindungen in FprEN 1993-1-8:2023 - 6.9(4). Diese Anforderung wird für beidseitige Kehlnähte überprüft durch:

\[a/t=\frac{\beta_w\gamma_{M2} f_y}{\sqrt{2} f_u \gamma_{M0} } \cdot \min \left \{1.0, 1.1\frac{f_y}{f_u} \right \}\]

wobei:

• \(a\) - Dicke der Schweißnahtkehle
• \(t\) - Dicke des durch die Kante verbundenen Blechs
• \(\beta_w\) - Korrelationsfaktor der Schweißnaht
• \(\gamma_{M2}\) - Sicherheitsfaktor für Bolzen und Schweißnähte; editierbar im Code-Setup
• \(f_y\) - Streckgrenze des Blechs
• \(f_u\) - Bruchfestigkeit der Schweißnaht
• \(\gamma_{M0}\) - Sicherheitsfaktor für Bleche; bearbeitbar im Code-Setup

Die Dicke der Schweißnahtaussparung für einseitige Kehlnähte ist doppelt so groß wie die für zweiseitige Kehlnähte.

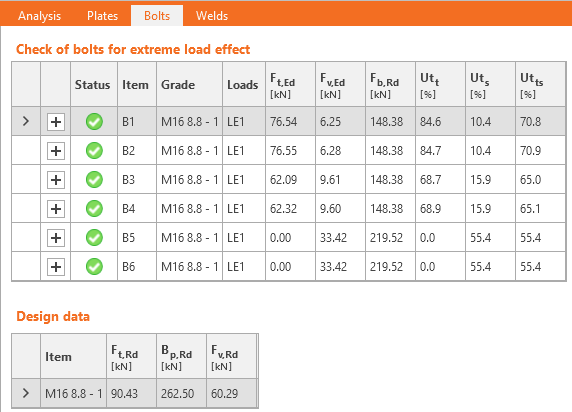
Nachweis von Schrauben und vorgespannten Schrauben nach Eurocode

Schrauben

Die Anfangssteifigkeit und die Bemessungstragfähigkeit von Schrauben bei Schub werden in CBFEM nach Abs. 3.6 und 6.3.2 in EN 1993-1-8 wiedergegeben. Die Feder, die Lochleibung und Zug darstellen, hat ein bilineares Kraft-Verformungs-Verhalten mit einer Anfangssteifigkeit und einer Bemessungstragfähigkeit nach Abs. 3.6 und 6.3.2 in EN 1993-1-8.

Bemessungswert der Zugtragfähigkeit der Schraube (EN 1993-1-8 – Tabelle 3.4):

\[ F_{t,Rd}=0,9 f_{ub} A_s / \gamma_{_M2} \]

Bemessungswert der Durchstanztragfähigkeit des Schraubenkopfes oder der Schraubenmutter (EN 1993-1-8 – Tabelle 3.4):

\[ B_{p,Rd} = 0,6 \pi d_m t_p f_u / \gamma_{M2} \]

Bemessungswert der Schertragfähigkeit je Scherebene (EN 1993-1-8 – Tabelle 3.4):

\[ F_{v,Rd} = \alpha_v f_{ub} A_s / \gamma_{M2} \]

Die Bemessungsschubtragfähigkeit kann mit dem Reduktionsfaktor β_p multipliziert werden, wenn ein Versatz vorhanden ist (EN 1993-1-8 – Abs. 3.6.1. (12)) und diese Option in den Normeinstellungen ausgewählt ist.

Bemessungswert der Lochleibungstragfähigkeit der Platte (EN 1993-1-8 – Tabele 3.4):

\( F_{b,Rd} = k_1 a_b f_u d t / \gamma_{M2} \)    für Standardlöcher

\( F_{b,Rd} = 0,6 k_1 a_b f_u d t / \gamma_{M2} \)    für Langlöcher

Ausnutzung bei Zug [%]:

\[ Ut_t = \frac{F_{t,Ed}}{\min (F_{t,Rd},\, B_{p,Rd})} \]

Ausnutzung bei Schub [%]:

\[ Ut_t = \frac{V}{\min (F_{v,Rd},\, F_{b,Rd})} \]

Interaktion von Zug und Schub [%]:

\[ Ut_{ts}=\frac{V}{F_{v,Rd}}+\frac{F_{t,Ed}}{1,4 F_{t,Rd}} \]

Wo:

• A_s – Zugspannungsfläche der Schraube
• f_ub – Zugfestigkeit der Schraube
• d_m – Mittelwert der Schnittpunkte und Schlüsselweiten des Schraubenkopfes oder der Mutter, je nachdem, welcher Wert kleiner ist
• d – Schraubendurchmesser
• t_p – Plattendicke unter dem Schraubenkopf/-mutter
• f_u – Stahlfestigkeit
• α_v = 0,6 für die Klasse 4.6, 5.6, 8.8 and 0,5 für die Klassen 4.8, 5.8, 6.8, 10.9
• \( k_1 = \min \left (2,8 \frac{e_2}{d_0}-1,7, \, 1,4 \frac{p_2}{d_0}-1,7, \, 2,5 \right ) \) – Faktor aus Tabelle 3.4
• α_b = 1,0 wenn der Lochleibungsnachweis mit a_b in den Normeinstellungen deaktiviert ist; bei aktiviertem Nachweis wird der Wert für α_b nach EN 1993-1-8 – Tabelle 3.4 ermittelt: \( \alpha_d = \min \left ( \frac{e_1}{3 d_0}, \, \frac{p_1}{3 d_0}-\frac{1}{4}, \, \frac{f_{ub}}{f_u} \right ) \)
• e₁, e₂ – Kantenabstände in Lastrichtung und senkrecht zur Lastrichtung
• p₁, p₂ – Schraubenabstände in Lastrichtung und senkrecht zur Lastrichtung
• F_t,Ed – Zugkraft (Bemessungswert) in der Schraube
• V – Scherkraft (Bemessungswert) in der Schraube
• γ_M2 – Sicherheitsfaktor (EN 1993-1-8 – Tabelle 2.1; änderbar in den Normeinstellungen)

Randabstände, die für die Schraubentragfähigkeit verwendet werden, müssen für allgemeine Plattengeometrien, Platten mit Öffnungen, Ausschnitten usw. relevant sein.

Der Algorithmus liest die tatsächliche Richtung des resultierenden Schubkraftvektors in einer gegebenen Schraube und berechnet dann die Abstände, die für den Lochleibungsnachweis benötigt werden.

Die End- (e₁) und Randabstände (e₂) werden durch Aufteilen der Plattenkontur in drei Segmente bestimmt. Das Endsegment ist durch einen 60°-Bereich in Richtung des Kraftvektors gekennzeichnet. Die Kantensegmente werden durch zwei 65°-Bereiche senkrecht zum Kraftvektor definiert. Als End- oder Kantenabstand wird dann der kürzeste Abstand einer Schraube zu einem relevanten Segment genommen.

Die Abstände zwischen den Schraubenlöchern (p₁; p₂) werden ermittelt, indem die umgebenden Schraubenlöcher virtuell um die Hälfte ihres Durchmessers vergrößert werden und dann zwei Linien in Richtung und senkrecht zum Schubkraftvektor gezogen werden. Die Abstände zu den vergrößerten Schraubenlöchern, die von diesen Linien geschnitten werden, gehen dann als p₁ und p₂ in die Berechnung ein.

Vorgespannte Schrauben

Bemessungswert des Gleitwiderstand je Schraubenklasse 8.8 oder 10.9 (EN 1993-1-8, Abs. 3.9 – Gleichung 3.8):

\[ F_{s,Rd} =\frac{k_s n \mu (F_{p,C} - 0,8 F_{t,Ed})}{\gamma_{M3}} \]

Die Vorspannkraft (EN 1993-1-8 – Gleichung 3.7)

F_p,C = 0,7 f_ub A_s

Der Vorspannkraftfaktor 0,7 kann in den Normeinstellungen geändert werden.

Ausnutzung [%]:

\[ Ut_s = \frac{V}{F_{s,Rd}} \]

Wo:

• A_s – Zugspannungsfläche der Schraube
• f_ub – Zugfestigkeit
• k_s – Koeffizient (EN 1993-1-8 – Tabelle 3.6; k_s = 1 für normale Rundlöcher, k_s = 0,63 für Langlöcher)
• μ – Gleitfaktor, änderbar in den Normeinstellungen (EN 1993-1-8 – Tabelle 3.7)
• n – Anzahl der Reibflächen. Der Nachweis wird für jede Reibfläche separat berechnet
• γ_M3 – Sicherheitsfaktor (EN 1993-1-8 – Tabelle 2.1; änderbar in den Normeinstellungen – empfohlene Werte sind 1,25 für den Grenzzustand der Tragfähigkeit und 1,1 für den Nachweis im Grenzzustand der Gebrauchstauglichkeit)
• V – Scherkraft (Bemessungswert) in der Schraube
• F_t,Ed – Zugkraft (Bemessungswert) in der Schraube

Wird das Gleiten von vorgespannten Schrauben im Grenzzustand der Gebrauchstauglichkeit überprüft, sollten diese anschließend auf "Lochleibung - Interaktion Scherzug" umgestellt und auf den Grenzzustand der Tragfähigkeit überprüft werden.

Konstruktionsregeln

Das Überprüfen der Konstruktionsregeln von Schrauben wird durchgeführt, wenn die Option in den Normeinstellungen ausgewählt ist. Überprüft werden die Abmessungen von der Schraubenmitte zu den Plattenkanten und zwischen den Schrauben. Randabstand e = 1,2 und Schraubenabstand p = 2,2 werden in Tabelle 3.3 in EN 1993-1-8 empfohlen. Der Anwender kann beide Werte in den Normeinstellungen ändern.

Code-Kontrolle von Ankern (EN)

Four anchor bolt types are available:

• Straight (assumed post-installed)
• Washer plate - Circular (assumed cast-in)
• Washer plate - Rectangle (assumed cast-in)
• Hook (assumed cast-in)

The steel resistances are determined according to EN 1993-1-8 and EN 1992-4 for cast-in anchors and post-installed fasteners, respectively.

The concrete resistances are determined according to EN 1992-4.

In case of post-installed (straight) fasteners, pull-out failure, combined pull-out and concrete failure of bonded anchors, and concrete splitting failure are not checked due to missing information available only for the particular anchor and glue type from the anchor manufacturer.

In the Project settings, settings are available to activate/deactivate concrete cone breakout checks in tension and shear. If the concrete cone breakout check is not activated, it is assumed that the dedicated reinforcement is designed to resist the force. The magnitude of the force is provided in formulas. User may use link to Detail application to perform the checks of reinforced concrete.

Furthermore, the concrete can be set as cracked or uncracked. Uncracked concrete should be in permanent compression that prevents shrinkage cracks. The resistances of uncracked concrete are higher. 

Tensile steel resistance (EN 1993-1-8, Table 3.4)

Cast-in anchors are checked according to steel design code.

\[ F_{t,Rd} = \frac{c \cdot k_2 \cdot f_{ub} \cdot A_s}{\gamma_{M2}} \]

where:

• c – decrease in tensile resistance of bolts with cut thread according to EN 1993-1-8 – Cl. 3.6.1. (3) editable in Project Settings
• k₂ = 0.9 – factor for non-countersunk anchors 
• f_ub – anchor bolt ultimate tensile strength 
• A_s – anchor bolt tensile stress area
• \(\gamma_{M2}=1.25\) – partial safety factor for bolts (EN 1993-1-8, Table 2.1) editable in Project Settings

Tensile steel resistance (EN 1992-4, Cl. 7.2.1.3)

Post-installed fasteners are checked according to concrete design code

\[ N_{Rd,s} = \frac{N_{Rk,s}}{\gamma_{Ms}} \]

where:

• N_Rk,s = c ∙ A_s ∙ f_uk – characteristic resistance of a fastener in case of steel failure
• c – decrease in tensile resistance of bolts with cut thread according to EN 1993-1-8 – Cl. 3.6.1. (3) editable in Code setup
• A_s – anchor bolt tensile stress area
• f_uk – anchor bolt characteristic ultimate tensile strength 
• \(\gamma_{Ms}=1.2 \cdot \frac{f_{uk}}{f_{yk}} \ge 1.4\) – partial safety factor for steel failure in tension (EN 1992-4, Table 4.1)
• f_yk – anchor bolt characteristic yield strength

Concrete cone failure resistance of anchor or group of anchors (EN 1992-4, Cl. 7.2.1.4):

\[ N_{Rd,c} = \frac{N_{Rk,c}}{\gamma_{Mc}} \]

where:

• \(N_{Rk,c}=N_{Rk,c}^0 \cdot \frac{A_{c,N}}{A_{c,N}^0} \cdot \psi_{s,N} \cdot \psi_{re,N} \cdot \psi_{ec,N} \cdot \psi_{M,N}\) – characteristic resistance of a fastener, a group of fasteners and the tensioned fasteners of a group of fasteners in case of concrete cone failure
• \(N_{Rk,c}^0 = k_1 \sqrt{f_{ck}} h_{ef}^{1.5}\) – characteristic resistance of a single fastener placed in concrete and not influenced by adjacent fasteners or edges of the concrete member
• k₁ – factor taking into account concrete condition and anchor type; for cast-in headed anchors (with washer plates) k₁ = 8.9 for cracked concrete and k₁ = 12.7 for non-cracked concrete; for post-installed fasteners (straight anchors) k₁ = 7.7 for cracked concrete and k₁ = 11.0 for non-cracked concrete
• f_ck – characteristic concrete compressive cylinder strength
• h_ef – embedment depth of the anchor in concrete; for three or more close edges, EN 1992-4, Cl. 7.2.1.4 (8) applies and effective \(h'_{ef} = \max \left \{ \frac{c_{max}}{c_{cr,N}} \cdot h_{ef}, \, \frac{s_{max}}{s_{cr,N}} \cdot h_{ef} \right \}\) is used instead in formulas for N_Rk,c⁰, c_cr,N, s_cr,N, A_c,N, A_c,N⁰, ψ_s,N, and ψ_ec,N
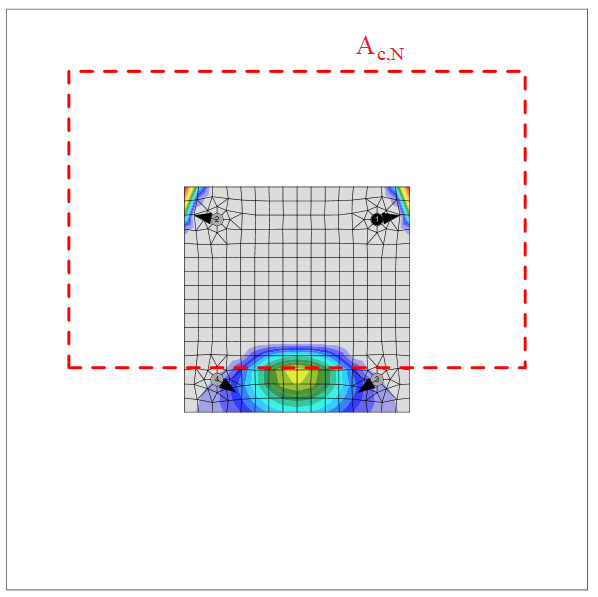
• A_c,N – actual projected area, limited by overlapping concrete cones of adjacent fasteners as well as by edges of the concrete member
• A_c,N⁰ = s_cr,N² – reference projected area, i.e. area of concrete of an individual anchor with large spacing and edge distance at the concrete surface 
• \(\psi_{s,N}=0.7+0.3 \cdot \frac{c}{c_{cr,N}} \le 1\) – factor taking into account disturbance of the distribution of stresses in the concrete due to the proximity of an edge of the concrete member
• c – smallest edge distance
• c_cr,N = 1.5 ∙ h_ef – characteristic edge distance for ensuring the transmission of the characteristic resistance of  an anchor in case of concrete break-out under tension loading
• \(\psi_{re,N}=0.5+\frac{h_{ef}}{200} \le 1\) – shell spalling factor
• \(\psi_{ec,N}=\frac{1}{1+2 \cdot (e_N / s_{cr,N})} \le 1\) – factor taking into account group effect when different tension loads are acting on the individual fasteners of a group; ψ_ec,N is determined separately for each direction and the product of both factors is used
• e_N – eccentricity of resultant tension force of tensioned fasteners in respect to the center of gravity of the tensioned fasteners
• s_cr,N = 2 ∙ c_cr,N – characteristic spacing of  anchors to ensure the characteristic resistance of the anchors  in case of concrete cone failure under tension load
• \(\psi_{M,N} = 2- \frac{z}{1.5 \cdot h_{ef}} \ge 1\) – factor taking into account effect of a compression force between fixture and concrete in cases of bending moments with or without axial force;  this parameter is equal to 1 if c < 1.5 h_ef or the ratio of the compressive force (including the compression due to bending) to the sum of tensile forces in anchors is smaller than 0.8 or z / h_ef ≥ 1.5 
• z – internal lever arm of a fastening
• γ_Mc = γ_c ∙ γ_inst – partial safety factor (EN 1992-4, Table 4.1)
• γ_c – partial safety factor for concrete (editable in Code setup)
• γ_inst – partial safety factor taking account of the installation safety of an anchor system (editable in Code setup)

The concrete breakout cone area for a group of anchors loaded by tension that creates a common concrete cone, A_c,N, is shown by the red dashed line.

Pull-out resistance (EN 1992-4, Cl. 7.2.1.5)

Pull-out resistance is checked for cast-in anchors with washer plates according to EN 1992-4, Cl. 7.2.1.5:

\[ N_{Rd,p}=\frac{N_{Rk,p}}{\gamma_{Mc}} \]

where:

• N_Rk,p = k₂ ∙ A_h ∙ f_ck – characteristic resistance in case of pull-out failure
• k₂ – coefficient dependent on concrete condition, k₂ = 7.5 for cracked concrete, k₂ = 10.5 for non-cracked concrete
• A_h – bearing area of head of anchor; for circular washer plate \(A_h = \frac{\pi}{4} \left ( d_h^2 - d^2 \right )\), for rectangular washer plate \(A_h = a_{wp}^2 - \frac{\pi}{4} d^2\)
• d_h ≤ 6 t_h + d – diameter of the head of the fastener
• t_h – thickness of the head of the headed fastener
• d – diameter of the shank of the fastener
• f_ck – characteristic concrete compressive cylinder strength
• γ_Mc = γ_c ∙ γ_inst – partial safety factor (EN 1992-4, Table 4.1)
• γ_c – partial safety factor for concrete (editable in Code setup)
• γ_inst – partial safety factor taking account of the installation safety of an anchor system (editable in Code setup)

Pull-out resistance (EN 1992-1-1, Cl. 8.4.4)

Pull-out resistance is checked for cast-in anchors with hook according to EN 1992-1-1, Cl. 8.4.4. Plain rods are assumed that require double anchorage length than ribbed reinforcement (Table 3.26 in BS 8110-1).

\[N_{Rd,p}=A_a \cdot f_{ya} \cdot \frac{l_b}{l_{bd}}\]

where:

• A_a – tensile stress area of an anchor
• f_ya – anchor yield strength
• l_b – anchor length embedded in concrete
• \(l_{bd} = \alpha_1 \cdot \alpha_2 \cdot \alpha_3 \cdot \alpha_4 \cdot \alpha_5 \cdot l_{b,rqd}\) – design anchorage length
• \(\alpha_1\) – factor for the effect of the shape of the bars assuming adequate cover
  • \(\alpha_1 = 0.7\) for \(c_d > 3 \phi\)
  • \(\alpha_1 = 1.0\) for \(c_d \le 3 \phi\)
• \(c_d = \min \{a/2, c_1\}\) – adequate cover
• a – clear distance between anchors
• c₁ – clear distance to concrete block edge
• \(\phi\) – anchor diameter
• \(\alpha_2 = 1.0 - 0.15 \frac{c_d - \phi}{\phi}\) – factor for the effect of concrete minimum cover; \(0.7 \le \alpha_2 \le 1.0\)
• \(\alpha_3 = 1.0\) – factor for the effect of confinement by transverse reinforcement
• \(\alpha_4 = 1.0 \) – factor for the influence of one or more welded transverse bars along the design anchorage length
• \(\alpha_5=1.0\) – factor for the effect of the pressure transverse to the plane of splitting along the design anchorage length
• \(l_{b,rqd} = \frac{\phi}{4} \frac{f_{ya}}{f_{bd}}\) – required anchorage length
• \(f_{bd} = \frac{2.25 \cdot \eta_1 \cdot \eta_2 f_{ctd}}{2}\) – design value of the ultimate bond stress (assumed half that of ribbed reinforcement)
• \(\eta_1=1.0\) – coefficient related to the quality of the bond condition and the position of the bar during concreting; good conditions are assumed, which may be dangerous for the rare case of horizontal anchors placed at the top of the concrete
• \(\eta_2=\min \{1.0, \frac{132-\phi}{100}\) – coefficient related to the bar diameter
• \(f_{ctd}=\frac{\alpha_{ct} \cdot f_{ctk,0.05}}{\gamma_c}\) – design value of concrete tensile strength
• \(\alpha_{ct}=1.0\) – coefficient taking account of long term effects on the tensile strength and of unfavourable effects
• \(f_{ctk,0.05}\) – characteristic axial tensile strength of concrete (5% quantile)
• \(\gamma_c\) – safety factor for concrete editable in Project Settings

Several detailing rules are added:

• Anchor yield strength must not be higher than 300 MPa (EN 1993-1-8 – 6.2.6.12 (5))
• Minimum anchorage length \(l_{b,min}\) must be kept (EN 1992-1-1 – Equation (8.6)):

\[ l_b \ge l_{b,min} = \max \{ 0.3 \cdot l_{b,rqd}, 10\cdot \phi , 100 \}\]

• Anchorage length should be sufficient for the steel tensile failure mode to govern to facilitate plastic design 

The pullout resistance of other types of anchors is not checked and must be guaranteed by the manufacturer.

Concrete blowout resistance (EN 1992-4, Cl. 7.2.1.8)

Blow-out failure is checked for cast-in headed anchors (Anchor type – washer) with edge distance c ≤ 0.5 h_ef according to EN 1992-4, Cl. 7.2.1.8. Anchors are treated as a group if their spacing near the edge is s ≤ 4 c₁. Undercut anchors can be checked the same way but the value of A_h is unknown in the software. The blow-out failure of undercut anchors can be determined by selecting a washer plate with the corresponding dimension.

\[N_{Rd,cb} = \frac{N_{Rk,cb}}{\gamma_{Mc}}\]

where:

• \(N_{Rk,cb} = N_{Rk,cb}^0 \cdot \frac{A_{c,Nb}}{A_{c,Nb}^0} \cdot \psi_{s,Nb} \cdot \psi_{g,Nb} \cdot \psi_{ec,Nb}\) – characteristic resistance in case of concrete blow-out failure
• \(N_{Rk,cb}^0 = k_5 \cdot c_1 \cdot \sqrt{A_h} \cdot \sqrt{f_{ck}}\) – characteristic resistance of a single fastener, not influenced by adjacent fasteners or further edges
• A_c,Nb – actual projected area, limited by overlapping concrete break-out bodies of adjacent fasteners as well as by proximity of edges of the concrete member or the member thickness
• A_c,Nb⁰ = (4 c₁)² – reference projected area of a single fastener with an edge distance equal to c₁
• \(\psi_{s,Nb} = 0.7+0.3 \frac{c_2}{2 c_1} \le 1\) – factor taking into account the disturbance of the distribution of stresses in the concrete due to the proximity of a corner of the concrete member
• \( \psi_{g,Nb} = \sqrt{n} + (1-\sqrt{n}) \frac{s_2}{4c_1} \ge 1 \) – factor taking into account group effect
• \(\psi_{ec,Nb} = \frac{1}{1+2 e_N / s_{cr,Nb}} \le 1\) – factor taking into account group effect, when different loads are acting on the individual fasteners of a group
• k₅ – parameter related to the state of the concrete; for cracked concrete k₅ = 8.7, for uncracked concrete k₅ = 12.2
• c₁ – edge distance of fastener in direction 1 towards the closest edge
• c₂ – edge distance of fastener perpendicular to direction 1 that is the smallest edge distance in a narrow member with multiple edge distances
• A_h – area of the load-bearing head of the fastener; for circular washer plate \(A_h = \frac{\pi}{4} \left ( d_h^2 - d^2 \right )\), for rectangular washer plate \(A_h = a_{wp}^2 - \frac{\pi}{4} d^2\)
• d – anchor nominal diameter
• d_h – circular washer plate diameter
• a_wp – side size of squared washer plate
• f_ck – characteristic compressive cylinder strength of concrete
• n – number of fasteners in a row parallel to the edge of the concrete member
• s₂ – spacing of fasteners in a group perpendicular to  direction 1
• s_cr,Nb = 4 c₁ – spacing that is required for a fastener to develop its characteristic tensile strength against blow-out failure

Anchor shear steel resistance (EN 1993-1-8 – Cl. 6.2.2)

Anchor shear steel resistance of cast-in anchors is determined according to EN 1993-1-8 – 6.2.2 (7) regardless of direct or mortar joint stand-off. The addition of friction is problematic in practice and is not assumed. The background for Eurocode calculation is the Stevin Laboratory model presented in this paper. Holes should be standard, not oversized and the grout strength and thickness should be according to Cl. 6.2.5 (7).

\[F_{vb,Rd} = \min \{F_{1vb,Rd}, F_{2vb,Rd} \} \]

where:

• \(F_{1vb,Rd} = \frac{\alpha_v \cdot f_{ub} \cdot A}{\gamma_{M2}}\) – anchor shear resistance from Table 3.4
  • α_v = 0.6 for grades 4.6, 5.6, 8.8 and 0.5 for grades 4.8, 5.8, 6.8, 10.9
  • f_ub – ultimate tensile strength of the bolt
  • A – tensile stress area of the bolt
    • A = A for shear plane excluded from threads; A is gross cross-section area of the anchor
    • A = A_s for shear plane intercepted by threads; A_s is tensile stress area of the bolt
  • γ_M2 – safety factor (EN 1993-1-8 – Table 2.1; editable in Project Settings)
• \(F_{2vb,Rd} = \frac{\alpha_b \cdot f_{ub} \cdot A_s}{\gamma_{M2}}\) – anchor shear resistance from Equation (6.2)
  • \(\alpha_b = 0.44 - 0.0003 f_{yb}\) – coefficient depending on the yield strength the anchor bolt
  • f_yb – anchor yield strength; 235 MPa \(\le f_{yb} \le\) 640 MPa
  • f_ub – anchor tensile strength
  • A_s – tensile stress area

Anchor shear steel resistance (EN 1992-4 – Cl. 7.2.2.3)

Anchor shear steel resistance of post-installed fasteners is checked according to EN 1992-4 – Cl. 7.2.2.3. Friction is not taken into account. Shear with and without lever arm is recognized in dependence on base plate manufacturing operation settings. 

\[V_{Rd,s} = \frac{V_{Rk,s}}{\gamma_{Ms}}\]

For stand-off: direct, the shear without lever arm is assumed (EN 1992-4 – Cl. 7.2.2.3.1):

V_Rk,s = k₆ ∙ A_s ∙ f_uk – characteristic resistance of a single fastener in case of steel failure; or fasteners with a ratio h_ef / d_nom < 5 and a concrete compressive strength class < C20/25 the characteristic resistance V_Rk,s should be multiplied by a factor of 0.8.

For stand-off: mortar joint, the shear with lever arm is assumed (EN 1992-4 – Cl. 7.2.2.3.2):

\[V_{Rk,s}= \frac{\alpha_M \cdot M_{Rk,s}}{l_a}\]

where:

• k₆ = 0.6 for anchors with fuk ≤ 500 MPa; k₆ = 0.5 otherwise
• A_s – shear area of anchor;  if shear plane in a thread is selected, the area reduced by threads is used; otherwise, full shank area is used
• f_uk – anchor bolt ultimate strength
• α_M = 2 – full restraint is assumed (EN 1992-4 – Cl. 6.2.2.3)
• \( M_{Rk,s} = M_{Rk,s}^0 \left ( 1 - \frac{N_{Ed}}{N_{Rd,s}} \right ) \) – characteristic bending resistance of the anchor decreased by the tensile force in the anchor
• M_Rk,s⁰ = 1.2 W_el f_ub – characteristic bending resistance of the anchor (ETAG 001, Annex C – Equation (5.5b))
• \( W_{el} = \frac{\pi d^3}{32}\) – section modulus of the anchor
• d – anchor bolt diameter; if the shear plane in a thread is selected, the diameter reduced by threads is used; otherwise, nominal diameter, d_nom, is used
• N_Ed – tensile force in the anchor
• N_Rd,s – tensile resistance of the anchor
• l_a = 0.5 d_nom + t_mortar + 0.5 t_bp – lever arm
• t_mortar – thickness of mortar (grout)
• t_bp – thickness of the base plate
• γ_Ms = 1.0 ∙ f_uk / f_yk ≥ 1.25 for f_uk ≤ 800 MPa and f_yk / f_uk ≤ 0.8; γ_Ms = 1.5 otherwise – partial safety factor for steel failure (EN 1992-4 – Table 4.1)

Concrete pry-out failure (EN 1992-4 – Cl. 7.2.2.4):

\[ V_{Rd,cp}= \frac{V_{Rk,cp}}{\gamma_{Mc}} \]

where:

• V_Rk,cp = k₈ ∙ N_Rk,c – characteristic resistance of concrete pry-out failure
• k₈ = 1 for h_ef < 60 mm; k₈ = 2 for h_ef ≥ 60 mm (ETAG 001, Annex C – Cl. 5.2.3.3)
• N_Rk,c – characteristic resistance of a fastener, a group of fasteners, and the tensioned fasteners of a group of fasteners in case of concrete cone failure; all anchors are assumed to be in tension
• γ_Mc = γ_c – partial safety factor (EN 1992-4 – Table 4.1, γ_inst = 1.0 for shear loading)
• γ_c – partial safety factor for concrete (editable in Code setup)

Concrete edge failure (EN 1992-4 – Cl. 7.2.2.5):

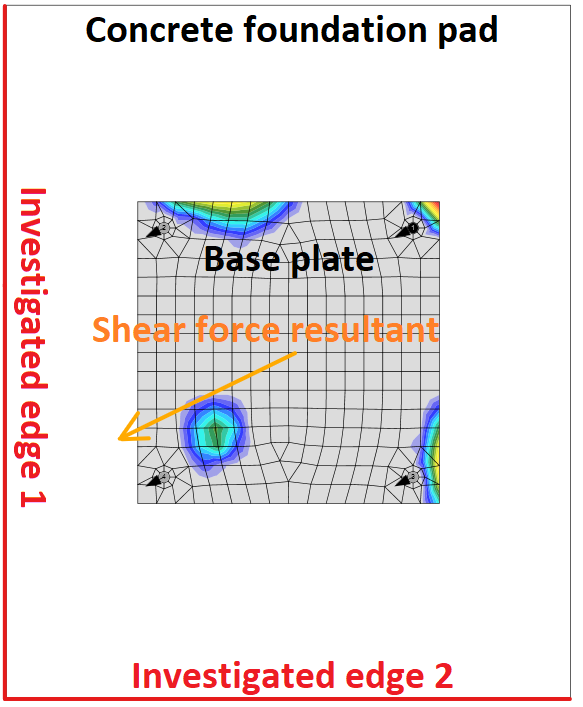
Concrete edge failure is a brittle failure, and the worst possible case is checked, i.e. only the anchors located near the edge transfer the full shear load acting on a whole base plate. If anchors are positioned in a rectangular pattern, the row of anchors at the investigated edge transfers the shear load. If anchors are positioned irregularly, the two anchors nearest to the investigated edge transfer the shear load. Two edges in the direction of the shear load are investigated, and the worst case is shown in the results.

Investigated edges in dependence on the direction of the shear force resultant

\[ V_{Rd,c} = \frac{V_{Rk,c}}{\gamma_{Mc}} \]

where:

• \( V_{Rk,c}= V_{Rk,c}^0 \cdot \frac{A_{c,V}}{A_{c,V}^0} \cdot \psi_{s,V} \cdot \psi_{h,V} \cdot \psi_{ec,V} \cdot \psi_{\alpha,V} \cdot \psi_{re,V} \) – characteristic resistance  of a fastener or a group of fasteners loaded towards the edge
• \( V_{Rk,c}^0 = k_9 \cdot d_{nom}^\alpha \cdot l_f^\beta \cdot f_{ck}^{0.5} \cdot c_1^{1.5}\) – initial value of the characteristic resistance of a fastener loaded perpendicular to the edge
• k₉ – factor taking into account concrete condition; k₉ = 1.7 for cracked concrete, k₉ = 2.4 for non-cracked concrete
• \( \alpha = 0.1 \left ( \frac{l_f}{c_1} \right ) ^{0.5} \)
• \( \beta = 0.1 \left ( \frac{d_{nom}}{c_1} \right ) ^{0.2} \)
• l_f = min (h_ef, 12 d_nom) for d_nom ≤ 24 mm; l_f = min [h_ef, max (8 d_nom, 300 mm)] for d_nom > 24 mm – effective length of the anchor in shear
• h_ef – embedment depth of the anchor in concrete
• c₁ – distance from the anchor to the investigated edge; for fastenings in a narrow, thin member, the effective distance \( c'_1=\max \left \{ \frac{c_{2,max}}{1.5}, \, \frac{h}{1.5}, \, \frac{s_{2,max}}{3} \right \} \) is used instead
• c₂ – smaller distance to the concrete edge perpendicular to the distance c₁
• d_nom – nominal anchor diameter
• A_c,V⁰ = 4.5 c₁² – area of a concrete cone of an individual anchor at the lateral concrete surface not affected by edges
• A_c,V – actual area of the concrete cone of the anchorage at the lateral concrete surface 
• \(\psi_{s,V} = 0.7+0.3 \frac{c_2}{1.5 c_1} \le 1.0 \) – factor which takes account of the disturbance of the distribution of stresses in the concrete due to further edges of the concrete member on the shear resistance
• \( \psi_{h,V} = \left ( \frac{1.5 c_1}{h} \right ) ^ {0.5} \ge 1.0 \) – factor which takes account of the fact that the shear resistance does not decrease proportionally to the member thickness as assumed by the ratio A_c,V / A_c,V⁰
• \( \psi_{ec,V} = \frac{1}{1+2 e_V / (3c_1)} \le 1 \) – factor which takes account of a group effect when different shear loads are acting on the individual anchors of a group
• \( \psi_{\alpha,V} = \sqrt{\frac{1}{(\cos \alpha_V)^2 + (0.5 \sin \alpha_V)^2}} \ge 1 \) – takes account of the angle α_V between the load applied, V, and the direction perpendicular to the free edge of the concrete member
• ψ_re,V = 1.0 – factor takes account of the effect of the type of reinforcement used in cracked concrete
• h – concrete block height
• γ_Mc = γ_c – partial safety factor (EN 1992-4 – Table 4.1, γ_inst = 1.0 for shear loading)
• γ_c – partial safety factor for concrete (editable in Code setup)

Interaction of tension and shear in steel (EN 1993-1-8 – Table 3.4)

The interaction of tension and shear for cast-in anchors is determined separately for steel and concrete. Steel failure mode is checked according to EN 1993-1-8 – Table 3.4. The interaction in steel is checked for each anchor separately.

\[ \frac{V_{Ed}}{F_{v,Rd}} + \frac{N_{Ed}}{1.4 \cdot F_{t,Rd}} \le 1.0 \]

Interaction of tension and shear in steel (EN 1992-4 – Table 7.3)

The interaction of tension and shear for post-installed fasteners is determined separately for steel and concrete failure modes according to Table 7.3. Interaction in steel is checked according to Equation (7.54). The interaction in steel is checked for each anchor separately.

\[ \left ( \frac{N_{Ed}}{N_{Rd,s}} \right )^2 + \left ( \frac{V_{Ed}}{V_{Rd,s}} \right )^2 \le 1.0 \]

Interaction of tension and shear in concrete

 Interaction in concrete is checked according to Equation (7.55).

\[ \left ( \frac{N_{Ed}}{N_{Rd,i}} \right )^{1.5} + \left ( \frac{V_{Ed}}{V_{Rd,i}} \right )^{1.5} \le 1.0 \]

The largest value of \(N_{Ed} / N_{Rd,i} \) and \(V_{Ed} / V_{Rd,i} \) for the different failure modes shall be taken. Note that values of \(N_{Ed}\) and \(N_{Rd,i}\) often belong to a group of anchors.

Anchors with stand-off

An anchor with stand-off is designed as a bar element loaded by shear force, bending moment, and compressive or tensile force. These internal forces are determined by the finite element model. The anchor is fixed on both sides, one side is 0.5×d below the concrete level, and the other side is in the middle of the thickness of the plate. The buckling length is conservatively assumed as twice the length of the bar element. Plastic section modulus is used. The bar element is designed according to EN 1993-1-1. The shear force may decrease the yield strength of the steel according to Cl. 6.2.8 but the minimum length of the anchor to fit the nut under the base plate ensures that the anchor fails in bending before the shear force reaches half the shear resistance. The reduction is therefore not necessary. The interaction of bending moment and compressive or tensile strength is assessed according to Cl. 6.2.1.

Shear resistance (EN 1993-1-1 Cl. 6.2.6):

\[ V_{pl,Rd} = \frac{A_V f_y / \sqrt{3}}{\gamma_{M2}} \]

where:

• A_V = 0.844 A_s – shear area
• A_s – bolt area reduced by threads
• f_y – bolt yield strength
• γ_M2 – partial safety factor

Tensile resistance (EN 1993-1-8 – Cl. 3.6.1):

\[ F_{t,Rd}=\frac{c k_2 f_{ub} A_s}{\gamma_{M2}} \ge F_t \]

where:

• c – decrease in tensile resistance of bolts with cut thread according to EN 1993-1-8 – Cl. 3.6.1. (3) editable in Code setup
• k₂ = 0.9 – factor from Table 3.4 in EN 1993-1-8
• f_ub – anchor bolt ultimate strength
• A_s – anchor bolt tensile stress area
• γ_M2 – safety factor (EN 1993-1-8 – Table 2.1; editable in Code setup)

Compressive resistance (EN 1993-1-1 Cl. 6.3):

\[ F_{c,Rd} = \frac{\chi A_s f_y}{\gamma_{M2}} \]

where:

• \( \chi = \frac{1}{\Phi + \sqrt{\Phi^2 - \bar\lambda^2}} \le 1 \) – buckling reduction factor
• \( \Phi = 0.5 \left [1+ \alpha (\bar\lambda - 0.2) + \bar\lambda^2 \right ] \) – value to determine buckling reduction factor χ
• α = 0.49 – imperfection factor for buckling curve c (belonging to the full circle)
• \( \bar\lambda = \sqrt{\frac{A_s f_y}{N_{cr}}} \) – relative slenderness
• \( N_{cr} = \frac{\pi^2 E I}{L_{cr}^2} \) – Euler's critical force
• \( I = \frac{\pi d_s^4}{64} \) – moment of inertia of the bolt
• L_cr = 2 l – buckling length; it is assumed on the safe side that the bolt is fixed in the concrete and able to rotate at the base plate freely
• l – length of the bolt element equal to half the base plate thickness + gap + half the bolt diameter; it is assumed on the safe side that the washer and a nut are not clamped to the concrete surface (ETAG 001 – Annex C – Cl. 4.2.2.4)

Bending resistance (EN 1993-1-1 Cl. 6.2.5):

\[ M_{pl,Rd} = \frac{W_{pl} f_y}{\gamma_{M2}} \]

• \( W_{pl}= \frac{d_s^3}{6} \) – section modulus of the bolt
• f_y – bolt yield strength
• γ_M2 – partial safety factor

Anchor steel utilization (EN 1993-1-1 Cl. 6.2.1)

\[ \frac{N_{Ed}}{N_{Rd}} + \frac{M_{Ed}}{M_{Rd}} \le 1 \]

where:

• N_Ed – tensile (positive) or compressive (negative sign) design force
• N_Rd – tensile (positive, F_t,Rd) or compressive (negative sign, F_c,Rd) design resistance
• M_Ed – design bending moment
• M_Rd = M_pl,Rd – design bending resistance

Detailing

A detailing check of anchors is performed if the option is selected in the Code setup. Only minimum spacing between anchors (measured centreline to centreline) is checked. The minimum spacing differs for each anchor type and is given in the European Technical Product Specification. Users can modify limit spacing value in the Code setup as a multiple of anchor bolt diameter.

Edge distances to steel plates follow the rules for bolts, i.e. e = 1.2 is recommended in Table 3.3 in EN 1993-1-8. User can modify this value in Code setup.

Nachweis des Betonblocks nach Eurocode

Beton unterhalb der Fußplatte wird vom Winkler-Untergrund mit gleichmäßiger Steifigkeit simuliert, die die Kontaktspannungen liefert. Für den Drucknachweis wird die nach EN 1993-1-8 ermittelte mittlere Spannung an der wirksamen Fläche verwendet.

Die Tragfähigkeit von Beton bei räumlichem Druck wird in Anlehnung an EN 1993-1-8 durch Berechnung der Bemessungstragfähigkeit des Betons im Anschluss f_jd unter der wirksamen Fläche A_eff der Fußplatte ermittelt. Die Bemessungstragfähigkeit des Anschlusses f_jd wird nach Abs. 6.2.5 in EN 1993-1-8 und Abs. 6.7 in EN 1992-1-1 ermittelt. Die Qualität und Dicke des Mörtels wird durch den Fugenbeiwert β_jd bestimmt. Für eine Mörtelqualität gleich oder besser als die Qualität des Betonblocks wird β_jd = 1,0 angenommen, EN 1993-1-8 empfiehlt den Wert β_jd = 0,67. Die wirksame Fläche A_eff,cm unter der Fußplatte wird als die Form des Stützenquerschnitts, vergrößert um zusätzliche Ausbreitungsbreite c, ermittelt.

\[ c = t \sqrt{\frac{f_y}{3 f_{jd} \gamma_{M0}}} \]

mit t als Dicke der Fußplatte, f_y der Streckgrenze der Fußplatte und γ_M0 als Teilsicherheitsbeiwert für Stahl.

Die wirksame Fläche wird durch Iteration berechnet, bis die Differenz zwischen den zusätzlichen Ausbreitungsbreiten der aktuellen und vorherigen Iteration |c_i – c_i–1 | weniger als 1 mm beträgt. Für die erste Iteration wird die Fläche der Fußplatte als tragende Fläche A_c0 angenommen.

Die Fläche, in der der Beton unter Druck steht, wird den Ergebnissen der FEM entnommen. Diese aus Druck belastete Fläche A_eff,FEM ermöglicht das Ermitteln der Position der neutralen Achse. Der Nutzer kann diese Fläche ändern, indem er in den Normeinstellungen „Wirksamer Bereich – Einfluss der Netzgröße“ bearbeitet. Der Standardwert ist 0,1, für den die Verifizierungsstudien durchgeführt wurden. Es wird nicht empfohlen, diesen Wert zu verringern. Eine Erhöhung dieses Wertes macht die Beurteilung der Betontragfähigkeit sicherer. Der Wert in den Normeinstellungen bestimmt die Grenze des Bereichs, A_eff,FEM, z.B. berücksichtigt der Wert von 0,1 nur Bereiche, in denen die Betonspannung größer ist als das 0,1-fache der maximalen Betonspannung, σ_c,max. Der Schnittpunkt der Druckfläche A_eff,FEM und der wirksamen Fläche A_eff,cm ermöglicht die Bewertung der Tragfähigkeit für eine allgemein belastete Fußplatten jeder Form mit beliebigen Versteifungen und wird mit A_eff bezeichnet. Die durchschnittliche Spannung σ auf der wirksamen Fläche, A_eff, wird als Druckkraft dividiert durch die wirksame Fläche bestimmt. Nachweis des Bauteils auf Spannungen mit σ ≤ f_jd.

Betontragfähigkeit bei konzentriertem Druck:

\[ f_{jd}= \beta_j k_j \frac{f_{ck}}{\gamma_c} \]

Konzentrationsfaktor unter Berücksichtigung der Erhöhung der Betondruckfestigkeit durch mehraxiale Spannung:

\[ k_j=\sqrt{\frac{A_{c1}}{A_{eff}}} \le 3,0 \]

mit A_c1 nach EN 1992-1-1 – Abs. 6.7. Die Fläche muss konzentrisch und geometrisch ähnlich der tragenden Fläche A_eff sein.

Durchschnittliche Spannung unter der Fußplatte:

\[ \sigma = \frac{N}{A_{eff}} \]

Ausnutzung bei Druck [%]:

\[ Ut = \frac{\sigma}{f_{jd}} \]

Wo:

• f_ck – Charakteristische Druckbetonfestigkeit
• β_j = 0,67 – Faktor der Mörtelqualität, änderbar in den Normeinstellungen
• γ_c – Sicherheitsfaktor für Beton
• A_eff – Wirksame Fläche, auf die sich die Normalkraft N verteilt

Die wirksame Fläche, A_eff,cm, berechnet nach EN für reinen Druck, ist mit einer gestrichelten Linie markiert. Die grafische Darstellung zeigt die Art der Überprüfung. Die berechnete wirksame Fläche A_eff,fem ist grün markiert. Die endgültige wirksame Fläche, A_eff, für den Nachweis der Kontaktspannung ist schraffiert hervorgehoben.

In seltenen Fällen, insbesondere bei nur durch Zugkraft belasteten Fußplatten (Druck im Beton wird durch Abstützkräfte verursacht) oder Zugkraft und Biegemoment, ist der Schnittpunkt der Flächen A_eff,cm und A_eff,fem sehr klein oder gar nicht vorhanden. In solchen Fällen sind die Druckkräfte im Allgemeinen sehr klein, der Nachweis liegt außerhalb des Geltungsbereichs des Eurocodes und der Beton unter Druck wird nicht nachgewiesen.

Netzsensitivität

Dieses Verfahren zur Beurteilung der Druckfestigkeit des Betons ist unabhängig vom Netz der Fußplatte, wie in den folgenden Abbildungen zu sehen ist. Sie wird am Beispiel von Beton in der Druckbemessung nach EN gezeigt. Es wurden zwei Fälle untersucht: Belastung durch reinen Druck von 1200 kN und Belastung durch eine Kombination von Druckkraft 1200 kN und Biegemoment 90 kN.

Einfluss der Anzahl der Elemente auf die Vorhersage des Drucktragfähigkeit des Betons bei reinem Druck

Der Einfluss der Anzahl der Elemente auf die Vorhersage die Tragfähigkeit des Betons unter Druck bei Druck und Biegung

Schub im Betonblock

Schub in Betonblock kann auf eine der drei Arten übertragen werden:

• Reibung
  \( Ut = \frac{V}{V_{Rd}} \)
  V_rd = N * C_f
  
• Scherlasche
  \( Ut = \max \left ( \frac{V_y}{V_{Rd,y}}, \, \frac{V_z}{V_{Rd,z}}, \, \frac{V}{V_{c,Rd}} \right ) \) \(V_{Rd,y} = \frac{A_{Vy} f_y}{\sqrt{3} \gamma_{M0}} \)
  \( V_{Rd,z} = \frac{A_{Vz} f_y}{\sqrt{3} \gamma_{M0}} \)
  \( V_{c,Rd} = A \sigma_{Rd,max} \)
  Profildübel und Schweißnähte werden ebenfalls durch die FEM überprüft.
  
• Anker
  Der Nachweis erfolgt gemäß ETAG 001 - Anhang C

Wo:

• A_V,y, A_V,z – Scherflächen des Querschnitts der Scherlasche in Richtung der Achsen y und z
• f_y – Streckgrenze
• γ_M0 – Sicherheitsfaktor
• V_y – Scherkraftkomponente in der Ebene der Fußplatte in y-Achsrichtung
• V_z – Scherkraftkomponente in der Ebene der Fußplatte in z-Achsrichtung
• V – Scherkraft (Vektorsumme beider Scherkraftkomponenten)
• N – Kraft senkrecht zur Fußplatte
• C_f – Reibungskoeffizient zwischen Stahl und Beton/Mörtel; änderbar in den Normeinstellungen
• A = l * b – Projizierte Fläche der Scherlasche ohne den Bereich über der Betonoberfläche
• l – Länge der Scherlasche ohne den Bereich über der Betonoberfläche
• b – Projizierte Breite der Scherlasche in Richtung der Schubbelastung
• σ_Rd,max = k₁ * v'  * f_cd – Maximale Spannung, die an den Kanten des Knotens aufgebracht werden kann
• k₁ = 1 – Faktor (EN 1992-1-1 – Gleichung (6.60))
• v' = 1 – f_ck / 250 – Faktor (EN 1992-1-1 – Gleichung (6.57N))
• \( f_{cd} = \alpha_{cc} \frac{f_{ck}} {\gamma_c} \) – Bemessungsdruckfestigkeit des Betons
• α_cc – Koeffizient für Langzeitwirkungen auf die Druckfestigkeit von Beton
• f_ck – Charakteristische Druckfestigkeit des Betons
• γ_c – Sicherheitsfaktor für Beton

Kapazitätsbemessung nach Eurocode

Die Kapazitätsbemessung ist Teil eines Erdbebennachweises und stellt sicher, dass der Anschluss eine ausreichende Verformungskapazität aufweist.

Das Ziel der Kapazitätsbemessung besteht darin, zu bestätigen, dass ein Gebäude ein kontrolliertes duktiles Verhalten aufweist, um einen Einsturz bei einem Erdbeben auf Konstruktionsebene zu vermeiden. Es wird erwartet, dass ein plastisches Gelenk in einem dissipativen Element auftreten, und alle nicht-dissipativen Elemente des Gelenks müssen in der Lage sein, Kräfte aufgrund des Nachgebens in dem dissipativen Element sicher zu übertragen. Das dissipative Element ist normalerweise ein momenttragfähiger Rahmen, kann aber auch z.B. eine Stirnplatte sein. Der Sicherheitsfaktor wird für dissipative Elemente nicht verwendet. Dem dissipativen Element werden zwei Faktoren zugeordnet:

• γ_ov – Überfestigkeitsfaktor – EN 1998-1, Abs. 6.2
  - Empfohlener Wert ist γ_ov = 1,25; änderbar in den Materialien
• γ_sh – Wiederverfestigungsfaktor – EN 1998-1
  - Empfohlene Werte sind γ_sh = 1,2 für Bauteile in momenttragfähigen Rahmen, ansonsten γ_sh = 1,0; änderbar in der Operation

Das Materialdiagramm wird gemäß der folgenden Abbildung modifiziert:

Die erhöhte Festigkeit des dissipativen Elements (f_y,max = f_y ⋅ γ_ov ⋅ γ_sh) ermöglicht die Eingabe von Lasten (M_y,Ed, V_z,Ed), die dazu führen, dass ein plastische Gelenk in dem dissipativen Element auftritt. Im Fall eines momenttragenden Rahmens und Bauteils als dissipatives Element sollte das Bauteil mit M_y,Ed = γ_ov ⋅ γ_sh ⋅ f_y ⋅ W_pl,y und der entsprechenden Querkraft V_z,Ed = –2 ⋅ M_y,Ed / L_h belastet werden, mit:

• f_y – Charakteristische Streckgrenze
• W_pl,y – Plastischer Widerstandsmodul
• L_h – Abstand zwischen plastischen Gelenken am Bauteil

Bei einem asymmetrischen Anschluss sollte das Bauteil sowohl durch durchhängende als auch durch ziehende Biegemomente und die entsprechenden Querkräfte belastet werden.

Die Platten von dissipativen Elementen sind vom Nachweis ausgeschlossen.

Beulanalyse nach Eurocode

Die Belastungstragfähigkeit schlanker Komponenten kann durch eine Kombination aus linearer Beulanalyse und materiell nichtlinearer Analyse bestimmt werden.

Es gibt fünf Kategorien der Finite-Elemente-Strukturanalyse mit folgenden Annahmen:

1. Lineares Material, geometrisch linear
2. Nichtlineares Material, geometrisch linear
3. Lineares Material, linearer Stabilitätsverlust – Beulen
4. Lineares Material, geometrisch nichtlinear mit Imperfektionen
5. Nichtlineares Material, geometrisch nichtlinear mit Imperfektionen

Ein Bemessungsverfahren, das die Ansätze 2 und 3 kombiniert - Material-Nichtlinearitäts- und Stabilitätsanalyse - wird in Kapitel 8 der EN 1993-1-6 genannt. Die Überprüfung der Beulfestigkeit auf der Grundlage der erhaltenen FEM-Ergebnisse ist in Anhang B der EN 1993-1-5 beschrieben. Dieses Verfahren wird für eine Vielzahl von Strukturen verwendet, mit Ausnahme von sehr schlanken Schalen, bei denen eine geometrisch nichtlineare Analyse mit anfänglichen Imperfektionen besser geeignet ist (4 und 5).

Das Verfahren verwendet Lastverstärker α, die als Ergebnisse der FEM-Analyse erhalten werden und die Vorhersage der Nachbeulfestigkeit der Anschlüsse ermöglichen.

Der Lastkoeffizient α_ult,k wird durch Erreichen der plastischen Kapazität, ohne Berücksichtigung der geometrischen Nichtlinearität, bestimmt. Die Überprüfung der plastischen Kapazität und die allgemeine automatische Bestimmung von α_ult,k ist in der Software implementiert.

Es wird der kritische Beulkfaktor α_cr ermittelt, der unter Verwendung einer FEM-Analyse der linearen Stabilität erhalten wird. Sie wird in der Software automatisch unter Verwendung des gleichen FEM-Modells wie für die Berechnung von α_ult,k ermittelt. Es ist zu beachten, dass der kritische Punkt, in Bezug auf den plastischen Widerstand, nicht unbedingt im ersten kritischen Beulmodus bewertet wird. In einem komplexen Anschluss müssen mehr Beulmodi bewertet werden, da sie sich auf verschiedene Teile des Anschlusses beziehen.

Die dimensionslose Plattenschlankheit \(\bar{\lambda_p} \) des untersuchten Beulmodus wird ermittelt durch:

\[ \bar \lambda_p = \sqrt{\frac{\alpha_{ult,k}}{\alpha_{cr}}} \]

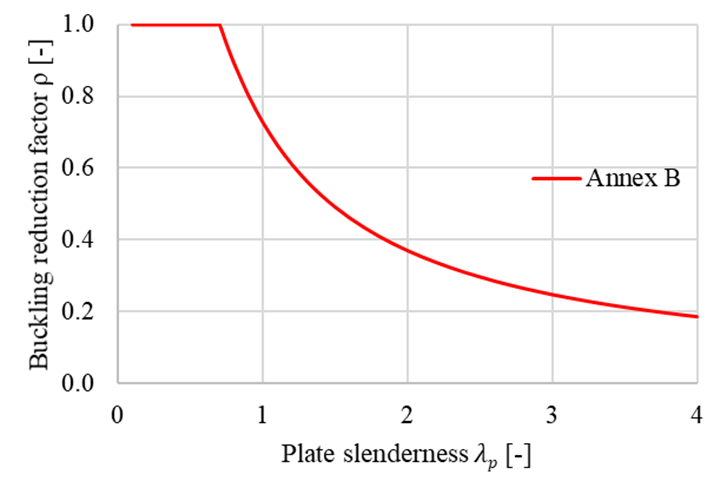
Der Beulreduktionsfaktor ρ wird gemäß Anhang B der EN 1993-1-5 ermittelt. Der Reduktionsfaktor hängt von der Plattenschlankheit ab. Die verwendete Beulkurve zeigt den Einfluss des Reduktionsfaktors auf die Plattenschlankheit. Der für ungleichmäßige Bauteile geltende Beulfaktor basiert auf den Beulkurven eines Trägers. Die Verifizierung basiert auf dem von Mises-Fließkriterium und der Methode der reduzierten Spannung. Der Beulwiderstand wird bewertet als

\[ \frac{\alpha_{ult,k} \rho}{\gamma_{M2}} \ge 1 \]

Beulreduktionsfaktor ρ gemäß EN 1993-1-5 Anhang B.

Obwohl der Prozess trivial erscheint, ist er allgemein, stabil und leicht zu automatisieren. Der Vorteil des Verfahrens ist die erweiterte FEM-Analyse der gesamten Verbindung, die auf die allgemeine Geometrie angewendet werden kann. Darüber hinaus ist es in den gültigen Eurocode-Standards enthalten. Die erweiterte numerische Analyse gibt einen schnellen Überblick über das globale Verhalten der Struktur und ihrer kritischen Teile und ermöglicht eine schnelle Versteifung, um Instabilitäten zu vermeiden.

Die Grenzschlankheit λ_p ist in Anhang B der EN 1993-1-5 angegeben und legt alle Fälle fest, die nach dem vorherigen Verfahren bewertet werden müssen. Der Widerstand wird durch Beulen für eine Plattenschlankheit von mehr als 0,7 begrenzt. Mit abnehmender Schlankheit wird der Widerstand durch plastische Beanspruchung bestimmt. Der kritische Grenzbeulfaktor für die Plattenschlankheit beträgt 0,7, und der Beulwiderstand (entspricht dem plastischen Widerstand) kann wie folgt erhalten werden

\[ \alpha_{cr} = \frac{\alpha_{ult,k}}{\bar \lambda_p^2} = \frac{1}{0.7^2} = 2.04 \]

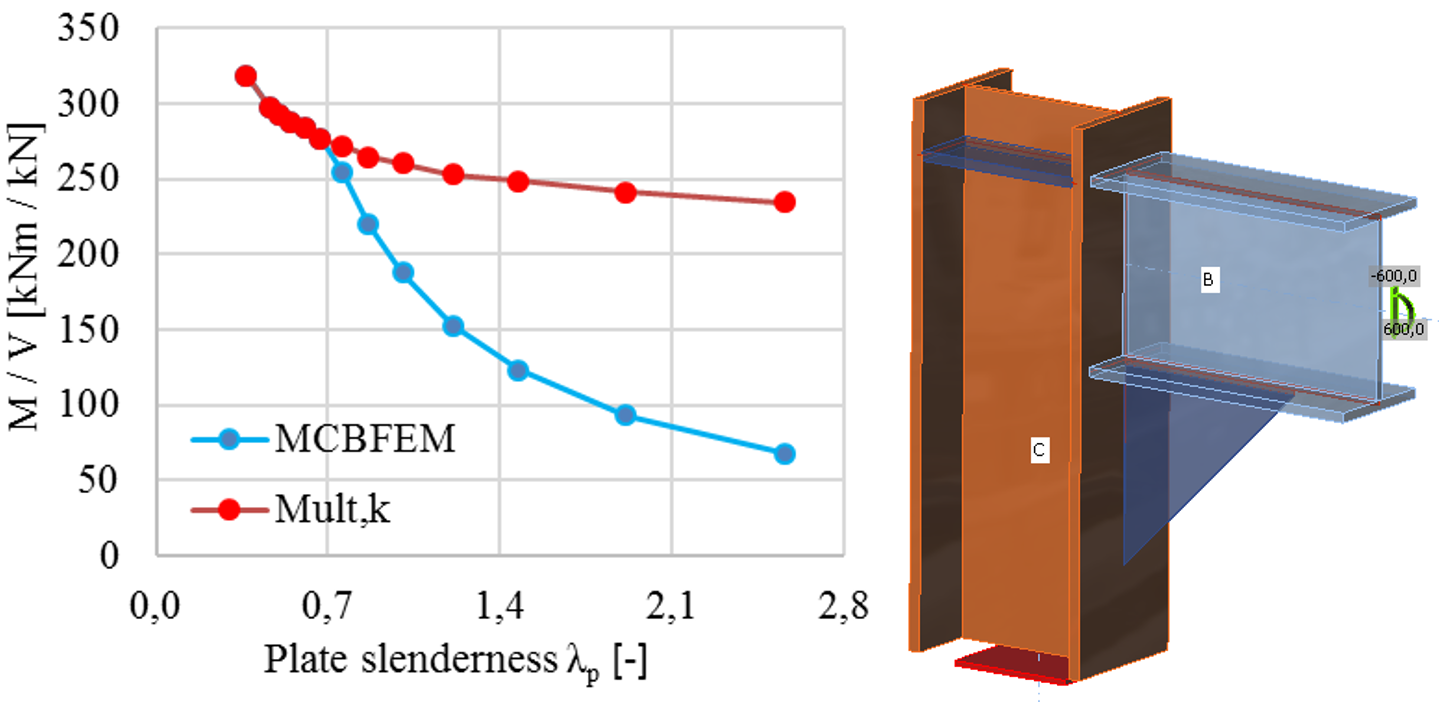
Der Einfluss der Plattenschlankheit auf den plastischen Widerstand M_ult,k und den Knickwiderstand M_CBFEM ist in der folgenden Abbildung dargestellt. Das Diagramm zeigt die Ergebnisse einer numerischen Untersuchung einer dreieckigen Steife in einer Portalrahmenverbindung.

Der Einfluss der Plattenschlankheit auf den Widerstand der Portalrahmenverbindung mit schlanker Steife

Anschlussklassifizierung (EN)

Anschlüsse werden nach Anschlusssteifigkeit klassifiziert in:

• Starr – Anschlüsse mit unbedeutender Änderung der ursprünglichen Winkel zwischen den Bauteilen,
• Halbstarr – Anschlüsse, von denen angenommen wird, dass sie in der Lage sind, ein zuverlässiges und bekanntes Maß an Biegesteifigkeit zu erbringen,
• Gelenkig – Anschlüsse, die keine Biegemomente entwickeln.

Anschlüsse werden EN 1993-1-8 – Abs. 5.2.2 klassifiziert in

• Starr – \( \frac{S_{j,ini} L_b}{E I_b} \ge k_b \)
• Halbstarr – \( 0.5 < \frac{S_{j,ini} L_b}{E I_b} < k_b \)
• Gelenkig – \( \frac{S_{j,ini} L_b}{E I_b} \le 0.5 \)

mit:

• S_j,ini – anfängliche Steifigkeit des Anschlusses; die Anschlusssteifigkeit wird bis auf 2/3 von M_j,Rd als linear angenommen
• L_b – Theoretische Länge des analysierten Bauteils; eingestellt in den Bauteileigenschaften
• E – Elastizitätsmodul
• I_b – Trägheitsmoment des analysierten Bauteils
• k_b = 8 für Rahmen, bei denen das Aussteifungssystem die horizontale Verschiebung um mindestens 80 % reduziert; k_b = 25 für andere Rahmen, sofern in jeder Etage K_b/K_c ≥ 0,1. Der Wert k_b = 25 wird verwendet, es sei denn, der Nutzer stellt in den Normeinstellungen "ausgesteiftes System" ein.
• M_j,Rd – Momententragfähigkeit des Anschlusses
• K_b = I_b / L_b
• K_c = I_c / L_c

Horizontale Zugverankerung

Verbindungen müssen so ausgelegt sein, dass sie Zugkräfte umwandeln, die durch Effekte zweiter Ordnung erzeugt werden – Stütze wird entfernt und der Boden wirkt als Membran.

Auflager

Es wird nur ein Bauteil analysiert und alle anderen Bauteile werden an ihren Enden fixiert. Auf das analysierte Bauteil sollte nur die Normalkraft aufgebracht werden, daher wird sein Modelltyp auf N-Vy-Vz eingestellt (Biegemomente und Torsion sind eingeschränkt).

Belastung

Die auf das analysierte Bauteil wirkende Normalkraft sollte gemäß EN 1993-1-7, Abs. A.5.1:

Für innere Bindungen:

\[T_i=0.8(g_k+\psi q_k) s L \ge 75 \textrm{ kN} \]

Für Randbindungen:

\[T_p=0.4(g_k+\psi q_k) s L \ge 75 \textrm{ kN} \]

Wo:

• \(g_k\) – Charakteristische ständige Last
• \(q_k\) – Charakteristische auferlegte Last
• \(s\) – Abstand der Bindungen
• \(L\) – Spannweite der Bindung
• \(\psi\) – relevanter Faktor im Ausdruck für eine Kombination von Schnittgrößen für die zufällige Bemessungssituation (z.B. \(\psi_1\) oder \(\psi_2\) gemäß Ausdruck (6.11b) in EN 1990).

Materialmodell und Nachweis

Gemäß SCI P358: Joints in steel construction: Simple Joints to Eurocode 3 – Anhang A, wird der Teilsicherheitsbeiwert für horizontale Zugverankerung eingeführt, \(\gamma_{Mu}\) mit Standardwert 1,1 änderbar in den Normeinstellungen. Dieser Sicherheitsfaktor wird für Bleche, Schrauben und Schweißnähte in der Analyse der horizontalen Zugverankerung verwendet.

Es werden extreme Belastungen und Verformungen erwartet und die Bemessung der Platten basiert auf der Höchstfestigkeit der Platten, \(f_u\). Deshalb verhält sich das Materialmodell für die Finite-Elemente-Analyse elastisch bis zu \(f_u / \gamma_{Mu}\). Die Steigung des plastischen Zweigs ist der Elastizitätsmodul von Young \(E/1000\). Es wird ein Nachweis auf eine plastische Dehnungsgrenze von 5% durchgeführt.

Die Widerstände von Schrauben und Schweißnähten werden mit \(\gamma_{Mu}\) anstelle von \(\gamma_{M2}\) berechnet. Bei Verwendung der Standardwerte der Teilsicherheitsbeiwerte liegen die Lastwiderstände um etwa 14% höher als im Grenzzustand der Tragfähigkeit.

Bei vorgespannten Schrauben wird davon ausgegangen, dass sie gleiten, und sie werden als normale, festsitzende Schrauben geprüft.

Referenzen

EN 1993-1-7: Eurocode 1 – Actions on structures – Part 1-7: General actions – Accidental actions, CEN, 2006

SCI P358: Joints in steel construction: Simple Joints to Eurocode 3

ECCS project FAILNOMORE workshops